 and
and 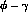 conversion factors,
conversion factors,
 (see eq.(38)), extracted from
(see eq.(38)), extracted from
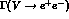
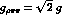 ,
,
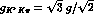
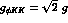 obtained from
obtained from 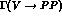
Our purpose in this section and the one to follow consists in attempting to go one step beyond the successful description of the low-energy interactions of the pseudoscalar-meson octet. This is done by refining the predictions of the above schemes through the introduction of a well-known effect in hadron physics, namely, SU(3)-breaking in the vector-meson sector, a refinement that forthcoming data will certainly require.
With the ``hidden symmetry" lagrangian discussed in sect. 2, one can attempt the description of the following sets of data (that we take from [13] neglecting error bars):
 and
and 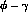 conversion factors,
conversion factors,
 (see eq.(38)), extracted from
(see eq.(38)), extracted from
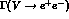
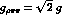 ,
,
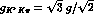
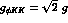 obtained from
obtained from 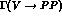
>From [30] we take the following experimental values for the electromagnetic (e.m.) charge radii
and the combined result, free from most systematic errors (see Dally et al. and Amendolia et al. in ref.[30])
The most immediate possibility to account for the above sets of
data consists
in using the ``hidden symmetry lagrangian'' (19)
as a self contained effective
theory in the good SU(3) limit. In this case, the SU(3)-breaking
effects shown by some of the above data remain unexplained but two
successful relations can be obtained for the non-strange sector.
The lagrangian (19) predicts 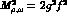 in the
in the
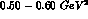 range when the values (65) for f are
used together with the range of values for g obtained from
range when the values (65) for f are
used together with the range of values for g obtained from
 (66) and
(66) and 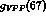 . This
agrees with the value coming from
the direct measurement of the
. This
agrees with the value coming from
the direct measurement of the
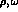 mass (64). Moreover, it also agrees with
that coming from the pion charge radius, leading
in our approach to
mass (64). Moreover, it also agrees with
that coming from the pion charge radius, leading
in our approach to  .
Alternatively, in a ChPT context, one can use
lagrangian (19) to saturate the finite part of the required
counterterms and then include the chiral-logs
from the loop corrections. One obtains [31]
( apart from the successful relation
.
Alternatively, in a ChPT context, one can use
lagrangian (19) to saturate the finite part of the required
counterterms and then include the chiral-logs
from the loop corrections. One obtains [31]
( apart from the successful relation
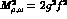 , as before ) a vanishing value for the
SU(3)-breaking low-energy counterterm
, as before ) a vanishing value for the
SU(3)-breaking low-energy counterterm 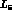 , eq.(6),
and
, eq.(6),
and  , eq. (5). With
this latter
value in (8) and evaluating the chiral-log correction at the
conventional value
, eq. (5). With
this latter
value in (8) and evaluating the chiral-log correction at the
conventional value 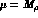 , one predicts
, one predicts  in very good agreement with the experimental
data (68).
in very good agreement with the experimental
data (68).
Including SU(3)-breaking effects, one can further improve this situation
[31].
Since the pseudoscalar sector is known to break the symmetry as in
eq.(4), 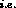 , proportionally to
, proportionally to
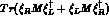 ,
we incorporate SU(3) symmetry breaking, as already attempted
in ref.[2],
via a similar hermitian combination
,
we incorporate SU(3) symmetry breaking, as already attempted
in ref.[2],
via a similar hermitian combination
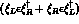 in both
in both 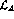 and
and 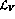 terms, i.e.,
terms, i.e.,
and
The matrix 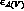 is taken to be
is taken to be 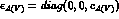 , where
, where 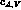 are the SU(3) -breaking real parameters to be determined. Notice that
the SU(3)-breaking terms,
are the SU(3) -breaking real parameters to be determined. Notice that
the SU(3)-breaking terms, 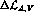 , are hermitian,
thus differing from those in ref.[2].
Fixing the unitary gauge
, are hermitian,
thus differing from those in ref.[2].
Fixing the unitary gauge  , (
, (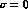 ), and expanding in terms of the pseudoscalar
fields, one observes
that the kinetic terms in
), and expanding in terms of the pseudoscalar
fields, one observes
that the kinetic terms in 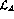 have to be renormalized. This
is simply achieved
rescaling the pseudoscalar fields [2]
have to be renormalized. This
is simply achieved
rescaling the pseudoscalar fields [2]
where an 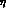 -
-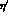 mixing angle of -
mixing angle of -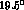 has been used for the
has been used for the 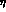 case.
case.
The physical content of this new, SU(3)-broken ``hidden symmetry''
lagrangian (70) and (71) can now be easily worked out.
>From 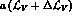 , we
obtain the conventional SU(3)-splitting for the
vector meson masses (a=2).
, we
obtain the conventional SU(3)-splitting for the
vector meson masses (a=2).
For the V-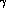 couplings,
the corresponding part of the lagrangian is explicitly given by:
couplings,
the corresponding part of the lagrangian is explicitly given by:
The new terms in the lagrangian (70,71) also induce an SU(3) symmetry
breaking in the 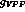 coupling constants.
One obtains
coupling constants.
One obtains
where the 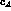 -dependence comes from the symmetry breaking in the
-dependence comes from the symmetry breaking in the
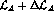 lagrangian due to the renormalization of the pseudoscalar fields
(see eq.(72)). This redefinition of the
pseudoscalar fields also implies symmetry breaking of their
decay constants, namely,
lagrangian due to the renormalization of the pseudoscalar fields
(see eq.(72)). This redefinition of the
pseudoscalar fields also implies symmetry breaking of their
decay constants, namely,
One can now attempt a description of the whole set of data (64-68) in
terms of, solely, the SU(3)-broken lagrangian (70) and (71).
This fixes the values of the two new free parameters to 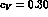 and
and 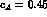 .
The fit is quite satisfactory for the four sets of data quoted in
eqs.(64) to (67).
For the pseudoscalar charge radii,
one gets from eqs.(74, 75, 76)
.
The fit is quite satisfactory for the four sets of data quoted in
eqs.(64) to (67).
For the pseudoscalar charge radii,
one gets from eqs.(74, 75, 76)
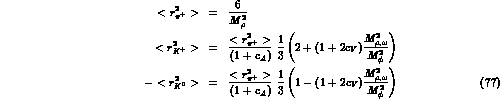
and the above values of  and
and 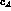 imply
imply
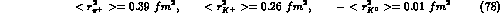
somewhat below (one or two  's) the experimental data
(68).
's) the experimental data
(68).
As
previously discussed, a more sophisticated possibility is
to use our SU(3)-broken lagrangian (70,71) in conjunction with ChPT.
This can only modify the predictions for 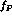 and
and 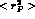 related to
processes without vector-mesons in the external legs. The chiral-logs
in eq.(7), evaluated at the conventional value
related to
processes without vector-mesons in the external legs. The chiral-logs
in eq.(7), evaluated at the conventional value 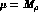 , account
now for some 35% of the observed difference between
, account
now for some 35% of the observed difference between 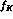 and
and
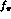 , thus requiring a smaller contribution from the
, thus requiring a smaller contribution from the 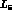 counterterm and, hence, a smaller value for
counterterm and, hence, a smaller value for  . Accordingly, the
best global fit is now achieved by the slightly modified values
. Accordingly, the
best global fit is now achieved by the slightly modified values
which preserve the goodness of the preceding fit for 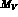 ,
,
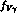 ,
, 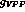 and
and 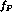 , while improving the agreement in
the
, while improving the agreement in
the 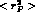 sector. Indeed, on the one hand, the chiral-logs in eq.(8) enhance the previous predictions for
sector. Indeed, on the one hand, the chiral-logs in eq.(8) enhance the previous predictions for 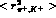 leading to
leading to
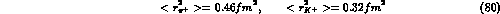
in better agreement with the data (68). On the other hand, making more explicit SU(3) breaking effects, one also obtains
which considerably improve the one-loop ChPT results [3] quoted in the
last line of eq.(8), namely 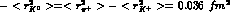 , significantly below the datum (69).
The reason for this
improvement stems from the fact that saturating the ChPT
counterterms with our SU(3)-broken lagrangian one goes beyond the
fourth order counterterms in ChPT, such as the SU(3)-symmetric counterterm
, significantly below the datum (69).
The reason for this
improvement stems from the fact that saturating the ChPT
counterterms with our SU(3)-broken lagrangian one goes beyond the
fourth order counterterms in ChPT, such as the SU(3)-symmetric counterterm
 , and introduces corrections from its SU(3)-breaking analogues
belonging to sixth order counterterm(s) in
, and introduces corrections from its SU(3)-breaking analogues
belonging to sixth order counterterm(s) in  . This is
explicitly seen in eqs.(81), which reduce to the conventional ChPT
result (8) only in the good SU(3) limit
. This is
explicitly seen in eqs.(81), which reduce to the conventional ChPT
result (8) only in the good SU(3) limit 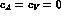 and
and
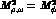 . We summarize the above in
Table 3, where we indicate the results obtained for
the charged radii in the
three models so far discussed, i.e. chiral perturbation theory (ChPT)
and SU(3) broken
``Hidden Symmetry'' (HS) scheme with and without chiral loops.
. We summarize the above in
Table 3, where we indicate the results obtained for
the charged radii in the
three models so far discussed, i.e. chiral perturbation theory (ChPT)
and SU(3) broken
``Hidden Symmetry'' (HS) scheme with and without chiral loops.
mm
One can easily extend the above results for the e.m. charge radii of
pseudoscalars to include their weak analogue in 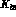 decays. Sirlin's
theorem [32], valid up to first order in SU(3)-breaking,
and requiring
decays. Sirlin's
theorem [32], valid up to first order in SU(3)-breaking,
and requiring
provides the clue. The data (68) and the
experimental value [13] 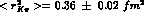 are fully compatible with Sirlin's theorem (82)
thus
reinforcing the significance of our discussion on charge radii (recall
that only one experiment has measured that for the neutral kaon). On the
other hand, the predictions of our first-order SU(3)-breaking
lagrangian verify (as they must) the theorem, thus checking our calculations
and providing their authomatic extension to the
are fully compatible with Sirlin's theorem (82)
thus
reinforcing the significance of our discussion on charge radii (recall
that only one experiment has measured that for the neutral kaon). On the
other hand, the predictions of our first-order SU(3)-breaking
lagrangian verify (as they must) the theorem, thus checking our calculations
and providing their authomatic extension to the 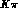 case. From the
expression
case. From the
expression
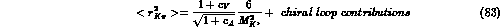
where the contribution from chiral loops is the one to be
found in ref. [3], we obtain
the very acceptable value 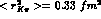 . The above equation
can be compared with the chiral perturbation
theory result [3]
. The above equation
can be compared with the chiral perturbation
theory result [3]
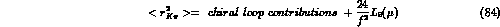
which gives 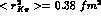 .
.