



Next: 4 Anomalous processes like
Up: Chapter 9 Section 4
Previous: 2 Role played by
In the previous section, we have discussed the implicit role played
by vector mesons in chiral
lagrangians, through saturation of the counterterm contributions. Beyond
the very low
energy region, where a lowest-order power expansion in 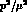 is sufficient, one may
try to extend the validity of chiral lagrangians through the
explicit introduction of vector meson fields. Two main lines
have been developed, the massive Yang Mills (YM) approach proposed by
Meissner
[1] among other authors, and the Hidden Symmetry (HS) scheme
proposed by Bando et al.
[2]. In the former, spin-1 fields are introduced in the
ungauged lagrangian
through the usual
covariant derivatives. Restricting, for simplicity of exposition, to the
sole SU(2) fields,
i.e. pions and
is sufficient, one may
try to extend the validity of chiral lagrangians through the
explicit introduction of vector meson fields. Two main lines
have been developed, the massive Yang Mills (YM) approach proposed by
Meissner
[1] among other authors, and the Hidden Symmetry (HS) scheme
proposed by Bando et al.
[2]. In the former, spin-1 fields are introduced in the
ungauged lagrangian
through the usual
covariant derivatives. Restricting, for simplicity of exposition, to the
sole SU(2) fields,
i.e. pions and 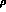 mesons, one starts with the usual lowest order
lagrangian
mesons, one starts with the usual lowest order
lagrangian
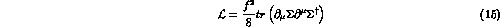
and then makes the substitution

where 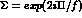 now contains only
the pion field
now contains only
the pion field  and
and 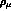 is
the
is
the 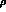 meson
field. This results in the lowest order lagrangian
meson
field. This results in the lowest order lagrangian
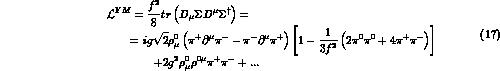
where, for the sake of the present argument, we have shown only some terms
involving
interactions between neutral 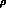 mesons and pions. The gauge
coupling constant
g is determined by neutral
mesons and pions. The gauge
coupling constant
g is determined by neutral 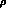 decay,
decay, 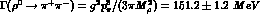 ,
to have the value
,
to have the value
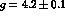 . In the massive Yang Mills scheme, photonic
interactions are then introduced through conventional Vector Meson Dominance,
i.e.
through the lagrangian
. In the massive Yang Mills scheme, photonic
interactions are then introduced through conventional Vector Meson Dominance,
i.e.
through the lagrangian
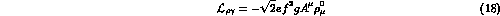
which mediates all transitions between photons and matter fields. Applying
this
rule to the decay 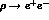 , one obtains the relation
, one obtains the relation
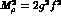 and
and 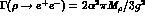 . The experimental values
. The experimental values 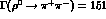 MeV and
MeV and
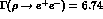 KeV are then fitted with
KeV are then fitted with  .
The dots in eq.(17) refer to further
quadratic interactions between
.
The dots in eq.(17) refer to further
quadratic interactions between 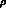 and an even number of pion
fields, but no mass terms
for the vector mesons. This is to be contrasted with what happens in the
lagrangian proposed by Bando et al.[2], in which the vector mesons
enter explicitly as gauge fields of a ``hidden'' local symmetry of the
chiral lagrangian, whereas the electro-weak gauge bosons are explicitly
introduced through the usual covariant derivatives. A Higgs-like
mechanism then generates the vector meson masses.
and an even number of pion
fields, but no mass terms
for the vector mesons. This is to be contrasted with what happens in the
lagrangian proposed by Bando et al.[2], in which the vector mesons
enter explicitly as gauge fields of a ``hidden'' local symmetry of the
chiral lagrangian, whereas the electro-weak gauge bosons are explicitly
introduced through the usual covariant derivatives. A Higgs-like
mechanism then generates the vector meson masses.
To wit, in the ``hidden symmetry approach'' of Bando et al.[2]
the most general lagrangian containing
pseudoscalar, vector and
(external) electroweak gauge fields with the smallest
number of derivatives, is given at the lowest order,
by the linear combination
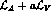 , a being an arbitrary parameter, of the
two SU(3) symmetric lagrangians
, a being an arbitrary parameter, of the
two SU(3) symmetric lagrangians
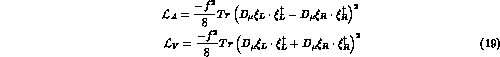
The matrices 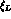 and
and 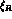 contain the
pseudoscalars fields, P, and the unphysical (or compensator)
scalar fields,
contain the
pseudoscalars fields, P, and the unphysical (or compensator)
scalar fields,  , that will be absorbed to give a mass to the
vector mesons
, that will be absorbed to give a mass to the
vector mesons
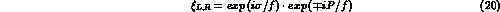
The full covariant derivative is
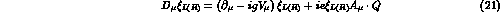
where only the photon field, 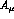 , (but not
its weak partners, as before)
has been explicitly shown, and P and V now stand for the
SU(3) octet and nonet matrices
, (but not
its weak partners, as before)
has been explicitly shown, and P and V now stand for the
SU(3) octet and nonet matrices
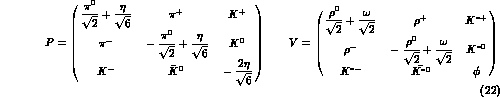
The lagrangian 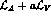 can be reduced to the
chiral lagrangian (1) for any value of the parameter a [2].
In fact, working in the unitary
gauge (
can be reduced to the
chiral lagrangian (1) for any value of the parameter a [2].
In fact, working in the unitary
gauge ( 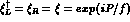 ) to eliminate the unphysical scalar fields and
substituting the
solution of the equation of motion for
) to eliminate the unphysical scalar fields and
substituting the
solution of the equation of motion for 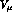 , the
, the
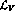 part vanishes
and
part vanishes
and 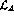 becomes identical to the non linear chiral lagrangian
(1).
becomes identical to the non linear chiral lagrangian
(1).
The ``hidden symmetry'' lagrangian 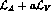 (19) can
be easily seen to contain, among other things, a vector meson mass
term, the pseudoscalar weak decay constants, the vector-photon
conversion
factor and the couplings of both vectors and photons to pseudoscalar
pairs. The latter can be eliminated fixing a = 2, thus incorporating
conventional vector-dominance in the electromagnetic form-factors
of pseudoscalars. Returning, as before,
to the simpler SU(2) case, for
(19) can
be easily seen to contain, among other things, a vector meson mass
term, the pseudoscalar weak decay constants, the vector-photon
conversion
factor and the couplings of both vectors and photons to pseudoscalar
pairs. The latter can be eliminated fixing a = 2, thus incorporating
conventional vector-dominance in the electromagnetic form-factors
of pseudoscalars. Returning, as before,
to the simpler SU(2) case, for 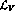 one has
one has
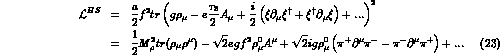
In the above equation, the constant a has been
fixed to the value a=2 in order to
recover the relation between 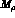 and the
and the 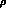 couplings, previously
discussed. This lagrangian obviously
reproduces all the lowest order results, as the previous one does,
however it does not
contain couplings between two or more
couplings, previously
discussed. This lagrangian obviously
reproduces all the lowest order results, as the previous one does,
however it does not
contain couplings between two or more 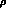 - mesons and an even number of
pion fields.
- mesons and an even number of
pion fields.
It is not yet clear if these two lagrangians are fully equivalent or not.
At first
sight, processes involving one 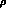 meson and four or more pion fields could
be used to discriminate between the two [9], since these
processes could proceed
through multiple
meson and four or more pion fields could
be used to discriminate between the two [9], since these
processes could proceed
through multiple 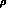 -pion interactions in the YM scheme, while not so
in the HS approach. However, it has been pointed out
that axial vector terms, not
yet introduced in the above lagrangians, would probably play a role. This
might render experimental discrimination rather difficult [10].
-pion interactions in the YM scheme, while not so
in the HS approach. However, it has been pointed out
that axial vector terms, not
yet introduced in the above lagrangians, would probably play a role. This
might render experimental discrimination rather difficult [10].
To the two schemes just discussed, one must also add the simplest and oldest of
them all, i.e. conventional Vector Meson Dominance
[11], in which
all photon-pseudoscalar interactions proceed through vector meson fields with
the same interaction lagrangian 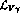 seen before and the
vector meson fields
are introduced through the covariant derivatives
in the free pion lagrangian
seen before and the
vector meson fields
are introduced through the covariant derivatives
in the free pion lagrangian 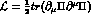 . The lagrangian thus obtained
. The lagrangian thus obtained
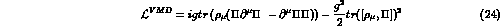
contains the same  vertices as the previous two, but there
are of course
no multipion interactions, which in conventional VMD are basically frozen into
the role played by the vector mesons.
vertices as the previous two, but there
are of course
no multipion interactions, which in conventional VMD are basically frozen into
the role played by the vector mesons.
After this brief introduction, we shall now discuss some vector meson
decay processes
which can be measured at DA NE , and in which the validity of the theoretical
scenarios we have illustrated can be tested.
NE , and in which the validity of the theoretical
scenarios we have illustrated can be tested.




Next: 4 Anomalous processes like
Up: Chapter 9 Section 4
Previous: 2 Role played by
Carlos E.Piedrafita
 is sufficient, one may
try to extend the validity of chiral lagrangians through the
explicit introduction of vector meson fields. Two main lines
have been developed, the massive Yang Mills (YM) approach proposed by
Meissner
[1] among other authors, and the Hidden Symmetry (HS) scheme
proposed by Bando et al.
[2]. In the former, spin-1 fields are introduced in the
ungauged lagrangian
through the usual
covariant derivatives. Restricting, for simplicity of exposition, to the
sole SU(2) fields,
i.e. pions and
is sufficient, one may
try to extend the validity of chiral lagrangians through the
explicit introduction of vector meson fields. Two main lines
have been developed, the massive Yang Mills (YM) approach proposed by
Meissner
[1] among other authors, and the Hidden Symmetry (HS) scheme
proposed by Bando et al.
[2]. In the former, spin-1 fields are introduced in the
ungauged lagrangian
through the usual
covariant derivatives. Restricting, for simplicity of exposition, to the
sole SU(2) fields,
i.e. pions and 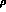 mesons, one starts with the usual lowest order
lagrangian
mesons, one starts with the usual lowest order
lagrangian
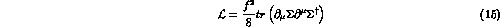

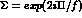 now contains only
the pion field
now contains only
the pion field  and
and 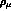 is
the
is
the 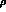 meson
field. This results in the lowest order lagrangian
meson
field. This results in the lowest order lagrangian
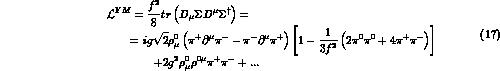
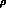 mesons and pions. The gauge
coupling constant
g is determined by neutral
mesons and pions. The gauge
coupling constant
g is determined by neutral 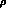 decay,
decay, 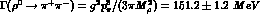 ,
to have the value
,
to have the value
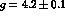 . In the massive Yang Mills scheme, photonic
interactions are then introduced through conventional Vector Meson Dominance,
i.e.
through the lagrangian
. In the massive Yang Mills scheme, photonic
interactions are then introduced through conventional Vector Meson Dominance,
i.e.
through the lagrangian
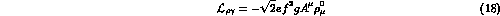
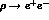 , one obtains the relation
, one obtains the relation
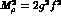 and
and 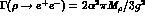 . The experimental values
. The experimental values 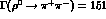 MeV and
MeV and
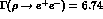 KeV are then fitted with
KeV are then fitted with  .
The dots in eq.(
.
The dots in eq.(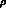 and an even number of pion
fields, but no mass terms
for the vector mesons. This is to be contrasted with what happens in the
lagrangian proposed by Bando et al.[
and an even number of pion
fields, but no mass terms
for the vector mesons. This is to be contrasted with what happens in the
lagrangian proposed by Bando et al.[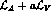 , a being an arbitrary parameter, of the
two SU(3) symmetric lagrangians
, a being an arbitrary parameter, of the
two SU(3) symmetric lagrangians
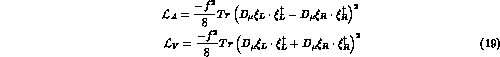
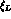 and
and 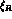 contain the
pseudoscalars fields, P, and the unphysical (or compensator)
scalar fields,
contain the
pseudoscalars fields, P, and the unphysical (or compensator)
scalar fields,  , that will be absorbed to give a mass to the
vector mesons
, that will be absorbed to give a mass to the
vector mesons
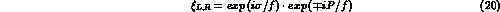
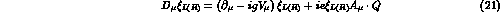
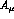 , (but not
its weak partners, as before)
has been explicitly shown, and P and V now stand for the
SU(3) octet and nonet matrices
, (but not
its weak partners, as before)
has been explicitly shown, and P and V now stand for the
SU(3) octet and nonet matrices
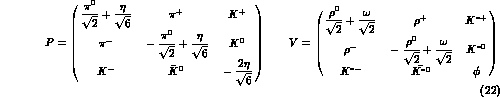
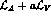 can be reduced to the
chiral lagrangian (
can be reduced to the
chiral lagrangian (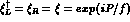 ) to eliminate the unphysical scalar fields and
substituting the
solution of the equation of motion for
) to eliminate the unphysical scalar fields and
substituting the
solution of the equation of motion for 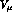 , the
, the
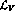 part vanishes
and
part vanishes
and 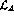 becomes identical to the non linear chiral lagrangian
(
becomes identical to the non linear chiral lagrangian
(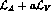 (
(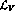 one has
one has
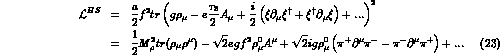
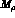 and the
and the 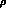 couplings, previously
discussed. This lagrangian obviously
reproduces all the lowest order results, as the previous one does,
however it does not
contain couplings between two or more
couplings, previously
discussed. This lagrangian obviously
reproduces all the lowest order results, as the previous one does,
however it does not
contain couplings between two or more 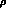 - mesons and an even number of
pion fields.
- mesons and an even number of
pion fields.
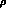 meson and four or more pion fields could
be used to discriminate between the two [
meson and four or more pion fields could
be used to discriminate between the two [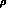 -pion interactions in the YM scheme, while not so
in the HS approach. However, it has been pointed out
that axial vector terms, not
yet introduced in the above lagrangians, would probably play a role. This
might render experimental discrimination rather difficult [
-pion interactions in the YM scheme, while not so
in the HS approach. However, it has been pointed out
that axial vector terms, not
yet introduced in the above lagrangians, would probably play a role. This
might render experimental discrimination rather difficult [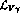 seen before and the
vector meson fields
are introduced through the covariant derivatives
in the free pion lagrangian
seen before and the
vector meson fields
are introduced through the covariant derivatives
in the free pion lagrangian 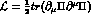 . The lagrangian thus obtained
. The lagrangian thus obtained
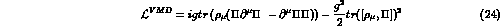
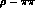 vertices as the previous two, but there
are of course
no multipion interactions, which in conventional VMD are basically frozen into
the role played by the vector mesons.
vertices as the previous two, but there
are of course
no multipion interactions, which in conventional VMD are basically frozen into
the role played by the vector mesons.
 NE , and in which the validity of the theoretical
scenarios we have illustrated can be tested.
NE , and in which the validity of the theoretical
scenarios we have illustrated can be tested.