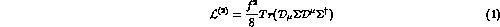
The inclusion of spin-1 mesons in effective chiral lagrangians has been largely discussed in the past and, with considerably renewed interest, during the last years. Indeed, traditional ideas associating spin-1 mesons with gauge bosons of local symmetries have been revisited and developed further. The so-called ``massive Yang-Mills approach'' and ``hidden symmetry scheme'' recently reviewed by Meissner [1] and Bando et al.[2] are two excellent and well detailed examples.
Conventional ChPT accounts for electro-weak and strong interactions of pseudoscalar mesons , P, in a perturbative series expansion in terms of their masses or four-momenta [3]. At lowest order in this expansion, the chiral lagrangian starts with the term
where the pion decay
constant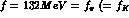 
, at this lowest-order level) and
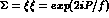with the matrix P given by
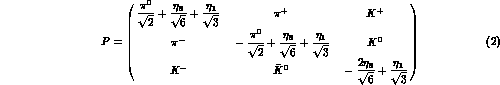
where, for later convenience, the singlet term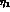 
has
been added to the conventional octet part (see Ametller's contribution to
this Handbook).
Electromagnetic interactions are contained in the covariant derivative
where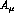 
is the photon field
(the
extension to weak interactions being trivial)
and Q is the quark-charge
matrix 
.
The mass degeneracy is broken via the additional mass term
with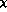 
containing the quark-mass matrix
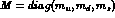and transforming
as a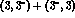 
representation of 
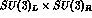. At
this lowest order, ChPT essentially coincides with Current Algebra.
The next order piece in the chiral expansion (fourth order) contains one-loop corrections with vertices from (1) to (4) and a series of ten counterterms required to cancel loop divergencies [3]. Some of them, e.g.,
are chiral-SU(3) symmetric, wheareas others, e.g.,
break the symmetry as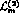 
in eq.(4). At this
one-loop
level, one obtains
[3]
where loop effects appear through the so-called chiral-logs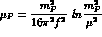 
. Similarly, the
pseudoscalar
electromagnetic charge-radii are found to be [3]
where, again, the divergencies accompaning the chiral-logs are absorbed
in one of the counterterms (or low-energy constants),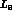 
,
appearing in
.
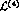The large number of low-energy constants one has to fix along the lines just discussed considerably reduces the predictive power of ChPT. For this reason, the attractive possibility that the values for those constants could be fixed assuming that they somehow parametrize the effects of the (so far ignored) exchange of the known meson resonances has been proposed [4] and successfully verified in many cases (see Chapter 3 in this Handbook for details). In most of them, particularly in processes involving the Wess-Zumino anomalous action, vector-mesons turn out to play the dominant role [5]. Their couplings to pseudoscalar plus photon states, as extracted from the experiments, saturate an important part of the above counterterms. Accurate effective lagrangians incorporating additional properties of vector mesons and further details on their dynamics could therefore be extremely useful not only as a self-contained effective theory but also as an auxiliary lagrangian fixing the counterterms in the ChPT context.
In order to illustrate the role played by vector mesons in saturating the
counterterms, we consider the case [6]
of the transition form factors controlling pseudoscalar
radiative
decays, i.e.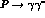 
, where P=
.
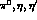The lowest order contribution to the corresponding amplitude F
comes from the Wess-Zumino term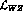 
at order 
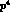and
is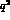 
independent (
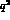being the mass of the off-shell photon). With the
on-shell normalization
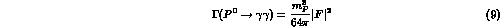
the lowest order amplitude reduces to (see section 3 for details)
where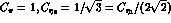 
and all the
decay
constants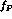 
are the same at this order. Loop corrections modify the
above result and introduce SU(3) breaking terms in the values for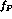 
.
As in the non-anomalous case, cancellation of the loop divergences
takes place through
appropriate counterterms and the remaining finite contribution leads to
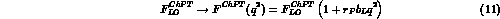
with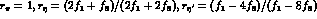 
(we have taken 
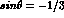for the 
-
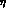mixing) and
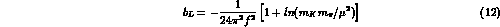
Fixing the scale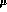 
at an average vector meson mass, i.e. 
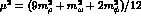, the loop contribution gives 
,
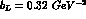a value too small to reproduce the experimental data for the slope,
as one can see
in the pion case, where one has[7]
.
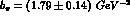Let us now consider the direct contribution from the vector mesons to this process. It can be obtained from VMD as a sum over all the poles, i.e.
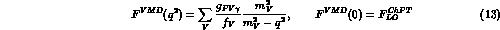
where the sum includes the contribution from the light vector mesons with SU(3)
symmetric
couplings to the photon,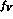 
, and to the meson-photon pair,
.
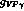In the good SU(3) limit the contribution from vector mesons is the same for all
the pseudoscalars, so that, expanding in powers
of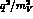 
, one can write
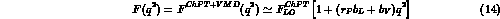
with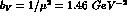 
. The entire
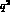dependence is parametrized in the low energy region through a
single slope parameter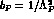 
and the values thus obtained
for 
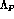, summing together chiral loops and vector meson
contributions, can be compared with experimental results with a very good
agreement (see sect. 8.1 in this Handbook). Noticing that the vector meson
contribution is
quite larger (by almost a factor 5) than the one from the loops, it is
clear that vector mesons are essential in reaching satisfactory agreement. It is
also evident that there is essentially no space left for additional
counterterm contributions, i.e. that vector mesons
dominate or ``saturate'' the counterterms.
Other
examples of how vector mesons saturate the counterterms in the chiral lagrangian have
been discussed in Chapters 3 and 8, as well as in ref. [8].
