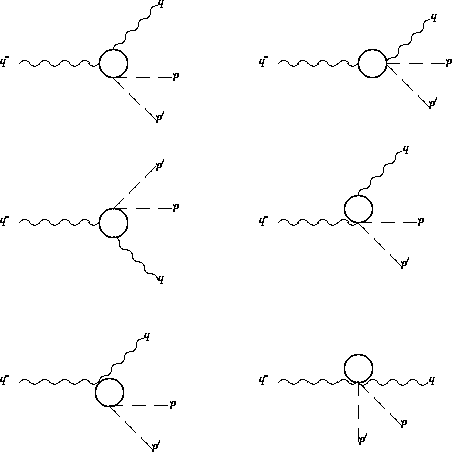
Figure 11: One loop diagrams for
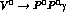 decays.
Charged-kaons or pions circulate along the loop
decays.
Charged-kaons or pions circulate along the loop
Let us now turn to the discussion of chiral loop contributions to the above processes. As mentioned, although strong, electromagnetic and weak interactions of pseudoscalar mesons P at low energies are known to be well described by effective chiral lagrangians, implementing the strict ChPT lagrangian with the effects of meson-resonances leads to a more complete and realistic scheme with a largely increased predictive power. In particular, it can incorporate and improve most of the VMD results so far discussed.

Figure 11: One loop diagrams for 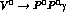 decays.
Charged-kaons or pions circulate along the loop
decays.
Charged-kaons or pions circulate along the loop
For concreteness, let us consider
 decay for which a rather low branching ratio
should be expected (see Table 1). There is a two-fold reason
for that: neutral particles cannot radiate
copiously (bremsstrahlung) photons and,
moreover, the Zweig rule suppress
decay for which a rather low branching ratio
should be expected (see Table 1). There is a two-fold reason
for that: neutral particles cannot radiate
copiously (bremsstrahlung) photons and,
moreover, the Zweig rule suppress  -decays into pions. In the ChPT
context this double suppression is at once avoided through the contributions of
charged-kaon loops. If so, the smallness of the
-decays into pions. In the ChPT
context this double suppression is at once avoided through the contributions of
charged-kaon loops. If so, the smallness of the 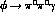 branching ratio will no longer hold and the analysis of this and related decays
could evidentiate the effects of the (otherwise elusive) chiral loops. Notice,
however, that we are pushing ChPT somewhat outside its original context
which did not allow for the inclusion of
branching ratio will no longer hold and the analysis of this and related decays
could evidentiate the effects of the (otherwise elusive) chiral loops. Notice,
however, that we are pushing ChPT somewhat outside its original context
which did not allow for the inclusion of  and other
resonances. Our purpose
is to compute some consequences of this extended version of ChPT to allow
for future comparison with experimental data.
and other
resonances. Our purpose
is to compute some consequences of this extended version of ChPT to allow
for future comparison with experimental data.
Using the SU(3)-extended terms of the lagrangians (17),(18) or (23)
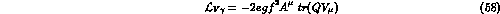
with 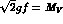 , the V-meson mass, or
, the V-meson mass, or  , we
now calculate the
ChPT-amplitudes for the decay processes
, we
now calculate the
ChPT-amplitudes for the decay processes  .
There is no tree-level contribution and at the
one-loop level one requires computing the set of diagrams shown in Fig.
(11). This leads to the amplitudes listed in sec.5 of
ref.[26]
and thus to the numerical contributions to the decay processes reported in
Table 2.
.
There is no tree-level contribution and at the
one-loop level one requires computing the set of diagrams shown in Fig.
(11). This leads to the amplitudes listed in sec.5 of
ref.[26]
and thus to the numerical contributions to the decay processes reported in
Table 2.
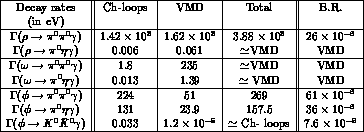
Table 2:
Contribution of Chiral loops and intermediate vector mesons to
decay rates (in eV) and branching ratios (last column) for different  transitions .
transitions .
Since VMD
amplitudes can be interpreted as saturating the ChPT counterterms,
the
above mentioned contributions have to be added to obtain the whole
ChPT amplitude. The relative weight of the two contributions
so far discussed --the finite
chiral loops versus the VMD amplitudes
(51)-- depends crucially on the decay mode.
Let us first discuss
 whose VMD contribution is given
by eqs.(51)
and (50) with the
whose VMD contribution is given
by eqs.(51)
and (50) with the  mass and width in both propagators. One
easily obtains[21]
mass and width in both propagators. One
easily obtains[21]
which is of the same order of magnitude as the pion-loop contribution
[26], 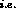
The global
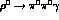 decay width is
therefore given by the sum of the two amplitudes leading separately to
eqs.(60) and (59). One obtains
decay width is
therefore given by the sum of the two amplitudes leading separately to
eqs.(60) and (59). One obtains
and the photonic spectrum shown (solid line) in Fig.(12) clearly
peaked at higher
energies  . The separated contributions from pion-loops and from
VMD, as well as their interference, are also shown in Fig.(12) (dashed,
dotdashed and dotted lines, respectively).
. The separated contributions from pion-loops and from
VMD, as well as their interference, are also shown in Fig.(12) (dashed,
dotdashed and dotted lines, respectively).
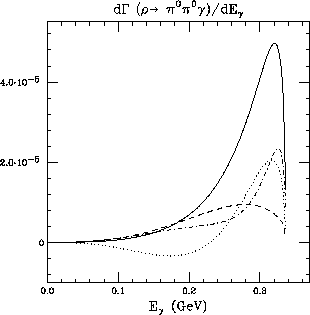
Figure 12: Photonic spectrum in 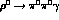 (solid line).
Dashed line corresponds to the contribution of pion-loops, dotdashed line is
the VMD contribution, and dotted line is their interference.
(solid line).
Dashed line corresponds to the contribution of pion-loops, dotdashed line is
the VMD contribution, and dotted line is their interference.
The situation changes quite clearly when turning to the other decay modes like
 ,
, 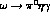 and
and 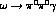 . We find that the
kaon-loop contributions are one or two
orders of magnitude smaller [26],
. We find that the
kaon-loop contributions are one or two
orders of magnitude smaller [26],
The physical reason for this suppression is that
the usually dominant pion-loops are isospin-forbidden in these decays. More
accurate estimates and the shape of the photonic spectra seem unnecessary due
to the smallness of the corresponding branching ratios (only the third one,
 , could reasonably
allow for detection) and also to the fact that these decay modes are dominated
by the well-understood (see [21]) but less-interesting VMD
contribution.
, could reasonably
allow for detection) and also to the fact that these decay modes are dominated
by the well-understood (see [21]) but less-interesting VMD
contribution.
By contrast the latter VMD-contribution is expected to be much smaller in
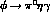 and
and  decays due to the Zweig
rule, as shown in Table 1,
well below the kaon-loop contributions,
decays due to the Zweig
rule, as shown in Table 1,
well below the kaon-loop contributions, 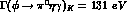 and
and 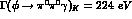 . Proceeding
as before and adding the corresponding amplitudes with the appropriate phases
leads to
. Proceeding
as before and adding the corresponding amplitudes with the appropriate phases
leads to
and the photonic spectra shown in Fig.(13) and (14).
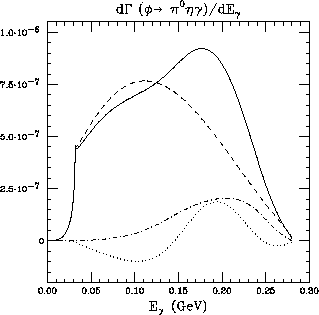
Figure 13: Photonic spectrum in 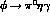 (solid line).
Dashed line corresponds to the contribution of kaon loops, dotdashed line is
the VMD contribution, and dotted line is their interference.
(solid line).
Dashed line corresponds to the contribution of kaon loops, dotdashed line is
the VMD contribution, and dotted line is their interference.
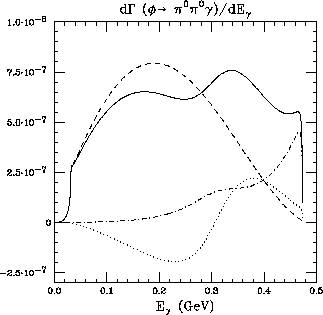
Figure 14: Photonic spectrum in  with
conventions as in Fig.(13).
with
conventions as in Fig.(13).
The Zweig allowed kaon-loops are
seen to dominate both spectra and decay rates of the above  -decays
and the predicted branching
ratios are large enough to allow for detection and analyses in future
-decays
and the predicted branching
ratios are large enough to allow for detection and analyses in future
 -factories. For completeness we have also computed
-factories. For completeness we have also computed
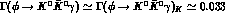 eV, with
eV, with 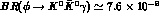 ,
again dominated by kaon-loops (due to the smallness of the VMD contribution
discussed in detail before and in ref. [21]). Notice that our
computation does not include scalar meson contributions, wich are expected to
be of the same order of magnitude [27,28,29]. Our results
represent therefore a well defined background to these latter, more interesting
contributions.
,
again dominated by kaon-loops (due to the smallness of the VMD contribution
discussed in detail before and in ref. [21]). Notice that our
computation does not include scalar meson contributions, wich are expected to
be of the same order of magnitude [27,28,29]. Our results
represent therefore a well defined background to these latter, more interesting
contributions.
In summary, the well understood contributions of intermediate vector
mesons in 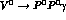 decays have been discussed. Vector
Meson Dominance alone predicts
decays have been discussed. Vector
Meson Dominance alone predicts
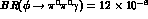 and
and
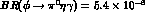 , and a characteristic
photonic
spectrum (peaked at higher energies) in the first decay. Similarly, an
exceptionally small contribution is predicted (and its physical origin
understood) for the branching ratio
, and a characteristic
photonic
spectrum (peaked at higher energies) in the first decay. Similarly, an
exceptionally small contribution is predicted (and its physical origin
understood) for the branching ratio
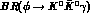 , namely,
, namely, 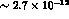 . Other
VMD predictions are
. Other
VMD predictions are 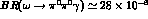 and
and 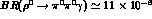 .
.
On the other hand, we find that some vector meson decays into two neutral
pseudoscalars and a
photon could receive important contributions from chiral loops if ChPT
is extended in the plausible and well defined
way proposed here. Some consequences of this extension --the relevance
of pion-loops in 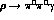 and the dominance of kaon-loops
in
and the dominance of kaon-loops
in 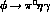 ,
,  -- have been unambigously
predicted thus allowing for future comparison with data. If the latter turn
out to confirm our predictions the domain of applicability of ChPT and
their relevance would be considerably increased.
-- have been unambigously
predicted thus allowing for future comparison with data. If the latter turn
out to confirm our predictions the domain of applicability of ChPT and
their relevance would be considerably increased.