



Next: References
Up: Chapter 9 Section 4
Previous: 6 SU(3)-breaking effects in
We shall now extend the above treatment
to processes related to the anomaly or Wess-Zumino
lagrangian. Notice that introducing our value 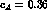 ,
eq.(79), in eq.(76) for
,
eq.(79), in eq.(76) for 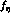 , leads to
, leads to 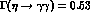 KeV quite in line with the datum [13]
KeV quite in line with the datum [13]
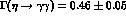 KeV. This encourages
to try a full treatment, similar to the
one discussed so far, to the anomalous sector.
Our purpose is to calculate the effects of
SU(3) symmetry breaking
in radiative decays of vector mesons, we have then to consider the
part of the Lagrangian related to the WZ anomaly and
we can expect, in analogy with what was done so far, that
these effects will require the introduction of
one more parameter in the discussion, which will be called
KeV. This encourages
to try a full treatment, similar to the
one discussed so far, to the anomalous sector.
Our purpose is to calculate the effects of
SU(3) symmetry breaking
in radiative decays of vector mesons, we have then to consider the
part of the Lagrangian related to the WZ anomaly and
we can expect, in analogy with what was done so far, that
these effects will require the introduction of
one more parameter in the discussion, which will be called
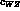 (see later). It will then be necessary to
reconsider all the successfull numerical tests obtained so far and
try to perform a single
global fit to both the anomalous and non-anomalous sector
with the three SU(3) breaking parameters
(see later). It will then be necessary to
reconsider all the successfull numerical tests obtained so far and
try to perform a single
global fit to both the anomalous and non-anomalous sector
with the three SU(3) breaking parameters
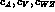 . We shall first proceed by obtaining
relations between the relevant couplings in the
anomalous sector and try to determine the parameters,
independently of what was done before.
. We shall first proceed by obtaining
relations between the relevant couplings in the
anomalous sector and try to determine the parameters,
independently of what was done before.
We start with vector--vector--pseudoscalar
meson (VVP) interactions as contained in the SU(3)-symmetric
VVP lagrangian introduced in ref. [2].
Inserting as before the additional, symmetry breaking term
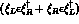 in an appropriate way to get an hermitian Lagrangian, the total
broken Lagrangian can now be written as
in an appropriate way to get an hermitian Lagrangian, the total
broken Lagrangian can now be written as
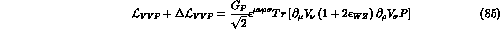
where  ,
, 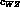 is the
breaking parameter in the anomalous sector, and
is the
breaking parameter in the anomalous sector, and
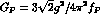 is the strong VVP coupling constant,
where the
is the strong VVP coupling constant,
where the 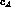 -dependent
-dependent 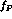 factor (see eq.(76))
already includes the part of the effects of SU(3)
breaking coming from the renormalization of the pseudoscalars fields
in the
factor (see eq.(76))
already includes the part of the effects of SU(3)
breaking coming from the renormalization of the pseudoscalars fields
in the 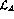 lagrangian.
lagrangian.
With this conventions,
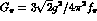 is the
is the
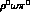 coupling constant (see section 4) which contains
no SU(3)-breaking and whose value can be obtained from the
experimental radiative decay width [13]
coupling constant (see section 4) which contains
no SU(3)-breaking and whose value can be obtained from the
experimental radiative decay width [13]
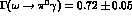 MeV.
MeV. 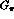 can also be obtained extracting
a value for
can also be obtained extracting
a value for 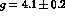 from
from 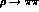 and
and 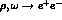 decay data [13].
Using
decay data [13].
Using 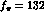 MeV, we then
obtain
MeV, we then
obtain 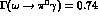 MeV in
good agreement with the experimental result.
In our normalization, the radiative decay widths
for vector mesons are given by
MeV in
good agreement with the experimental result.
In our normalization, the radiative decay widths
for vector mesons are given by
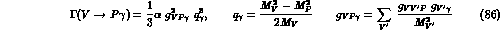
where the relevant coupling constants
take into account that these decays proceed via intermediate
vector mesons  . Thanks to this, one immediately recovers the
successful relation (10),
. Thanks to this, one immediately recovers the
successful relation (10), 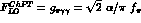 ,
coming from the WZ anomaly and satisfied by the experimental
,
coming from the WZ anomaly and satisfied by the experimental
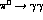 decay rate.
decay rate.
The coupling constants 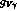 are easily
obtained from the lagrangian in eq.(74) defined in the
previous section. One then obtains
are easily
obtained from the lagrangian in eq.(74) defined in the
previous section. One then obtains
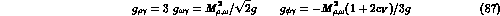
which are the SU(3) broken modifications of the usual 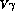 couplings with all equal masses (38).
It is interesting to see
how one can achieve both consistency with the
unbroken case successful relations as well as with
the experimental value of
the V-masses, if one choose a value for
the parameter
couplings with all equal masses (38).
It is interesting to see
how one can achieve both consistency with the
unbroken case successful relations as well as with
the experimental value of
the V-masses, if one choose a value for
the parameter 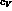 such that
such that
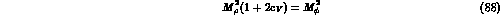
This is achieved by choosing 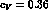 ,
not far from the range of values
for which a good fit to a large number of
other low energy constant was obtained in the previous section.
With this choice, we then have
,
not far from the range of values
for which a good fit to a large number of
other low energy constant was obtained in the previous section.
With this choice, we then have
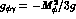 and using eqs.(86),
(87) and the broken VVP Lagrangian (85) to
extract the
and using eqs.(86),
(87) and the broken VVP Lagrangian (85) to
extract the 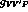 couplings, we obtain the
following expressions for the coupling constants
couplings, we obtain the
following expressions for the coupling constants 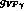
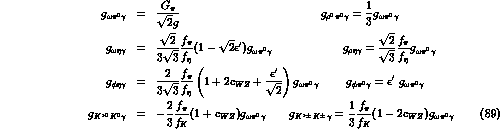
The parameter  is the one introduced in section 4,
eq.(49), to account for the small
contamination of
non--strange (strange) quarks in the
is the one introduced in section 4,
eq.(49), to account for the small
contamination of
non--strange (strange) quarks in the  (
( ) meson.
Notice that, because of eq.(88), the parameter
) meson.
Notice that, because of eq.(88), the parameter
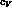 disappears from the above relations, which now contain only
disappears from the above relations, which now contain only
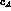 and
and 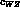 . The value of the anomalous breaking
parameter
. The value of the anomalous breaking
parameter
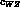 can be directly obtained
from the ratio between the experimental decay widths [13]
can be directly obtained
from the ratio between the experimental decay widths [13]
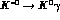 and
and 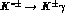 .
The ratio depends only from
.
The ratio depends only from 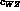 and leads immediately to
and leads immediately to
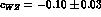 , whereas for
, whereas for 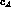 we can use eq.(76)
and the experimental results
we can use eq.(76)
and the experimental results
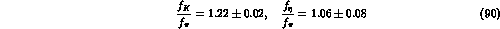
which lead to the value  as obtained in the previous
section.
as obtained in the previous
section.
At this point, the set of SU(3) breaking parameters
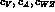 can be put to a test by calculating
the V radiative decay widths
following eq.(86) with the coupling
constants given by eq.(89).
Our results, obtained using
can be put to a test by calculating
the V radiative decay widths
following eq.(86) with the coupling
constants given by eq.(89).
Our results, obtained using 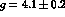 and
and
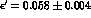 , as well as
, as well as 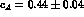 and
and
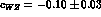 for the symmetry breaking parameters, are shown
in Table 4. For comparison we also
include the corresponding experimental decay widths as taken from
ref.[13] (in the
for the symmetry breaking parameters, are shown
in Table 4. For comparison we also
include the corresponding experimental decay widths as taken from
ref.[13] (in the 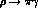 case we have averaged for
neutral and charged decays).
The description of all these data turns out to be quite satisfactory,
with SU(3)-breaking effects playing a central role in some cases. As
already noted by Hajuj [33], a non-vanishing value for
case we have averaged for
neutral and charged decays).
The description of all these data turns out to be quite satisfactory,
with SU(3)-breaking effects playing a central role in some cases. As
already noted by Hajuj [33], a non-vanishing value for 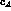 (thus achieving
(thus achieving 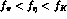 ) is essential to
reduce the predicted
) is essential to
reduce the predicted 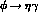 and
and 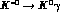 decay rates to their experimental values. Our value
decay rates to their experimental values. Our value 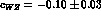 is also crucial to improve the results of ref.[33]
(particularly, for the
is also crucial to improve the results of ref.[33]
(particularly, for the 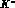 radiative decays) where such a source of
SU(3)-breaking has been neglected. As mentioned, the other SU(3)-breaking
parameter
radiative decays) where such a source of
SU(3)-breaking has been neglected. As mentioned, the other SU(3)-breaking
parameter 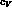 is fixed here so as to satisfy the relation
is fixed here so as to satisfy the relation
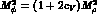 .
.
To enlarge our discussion, we have also tried to fit the
radiative decays with a different set of parameters. The choice,
which is shown in Table 4 was based on the use
of the set 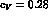 and
and  , which was
considered optimal in the previous section, when chiral
loop
contributions were added to the vector meson terms.
Notice that because the use of eq.(88) would introduce
an error in eqs.(89) for this value of
, which was
considered optimal in the previous section, when chiral
loop
contributions were added to the vector meson terms.
Notice that because the use of eq.(88) would introduce
an error in eqs.(89) for this value of 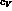 , we refrain
from using it in the whole set of those equations,
which now come to depends explicitly
upon the parameter
, we refrain
from using it in the whole set of those equations,
which now come to depends explicitly
upon the parameter 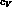 . On its turn, this
means that the whole numerical dependence of those equations upon
the parameters
. On its turn, this
means that the whole numerical dependence of those equations upon
the parameters 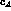 and
and 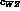 changes and we
obtain a different set of optimal values, which are
in line with the results of refs. [33] and [2], and
shown in last column of Table 4.
Again the
agreement is quite good and the decision of how
to optimize the use of our lagrangians remains open
waiting for improved data and analysis.
changes and we
obtain a different set of optimal values, which are
in line with the results of refs. [33] and [2], and
shown in last column of Table 4.
Again the
agreement is quite good and the decision of how
to optimize the use of our lagrangians remains open
waiting for improved data and analysis.
mm
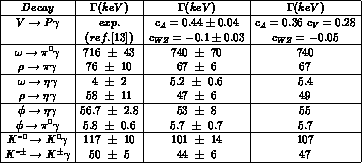
Table 4:
In summary, well-known SU(3)-breaking effects have been
shown to be easily introduced
in effective lagrangians incorporating vector-mesons. In
particular, the VVP interactions, related to radiative vector-meson
decays -- for which accurate new data are expected --
and to the anomalous
 decays,
are accurately described, improving
the results of previous related work [33].
decays,
are accurately described, improving
the results of previous related work [33].




Next: References
Up: Chapter 9 Section 4
Previous: 6 SU(3)-breaking effects in
Carlos E.Piedrafita
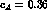 ,
eq.(79), in eq.(76) for
,
eq.(79), in eq.(76) for 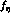 , leads to
, leads to 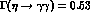 KeV quite in line with the datum [13]
KeV quite in line with the datum [13]
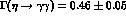 KeV. This encourages
to try a full treatment, similar to the
one discussed so far, to the anomalous sector.
Our purpose is to calculate the effects of
SU(3) symmetry breaking
in radiative decays of vector mesons, we have then to consider the
part of the Lagrangian related to the WZ anomaly and
we can expect, in analogy with what was done so far, that
these effects will require the introduction of
one more parameter in the discussion, which will be called
KeV. This encourages
to try a full treatment, similar to the
one discussed so far, to the anomalous sector.
Our purpose is to calculate the effects of
SU(3) symmetry breaking
in radiative decays of vector mesons, we have then to consider the
part of the Lagrangian related to the WZ anomaly and
we can expect, in analogy with what was done so far, that
these effects will require the introduction of
one more parameter in the discussion, which will be called
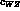 (see later). It will then be necessary to
reconsider all the successfull numerical tests obtained so far and
try to perform a single
global fit to both the anomalous and non-anomalous sector
with the three SU(3) breaking parameters
(see later). It will then be necessary to
reconsider all the successfull numerical tests obtained so far and
try to perform a single
global fit to both the anomalous and non-anomalous sector
with the three SU(3) breaking parameters
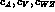 . We shall first proceed by obtaining
relations between the relevant couplings in the
anomalous sector and try to determine the parameters,
independently of what was done before.
. We shall first proceed by obtaining
relations between the relevant couplings in the
anomalous sector and try to determine the parameters,
independently of what was done before.
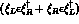 in an appropriate way to get an hermitian Lagrangian, the total
broken Lagrangian can now be written as
in an appropriate way to get an hermitian Lagrangian, the total
broken Lagrangian can now be written as
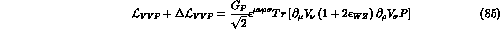
 ,
, 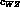 is the
breaking parameter in the anomalous sector, and
is the
breaking parameter in the anomalous sector, and
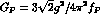 is the strong VVP coupling constant,
where the
is the strong VVP coupling constant,
where the 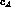 -dependent
-dependent 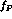 factor (see eq.(
factor (see eq.(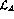 lagrangian.
lagrangian.
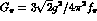 is the
is the
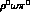 coupling constant (see section 4) which contains
no SU(3)-breaking and whose value can be obtained from the
experimental radiative decay width [
coupling constant (see section 4) which contains
no SU(3)-breaking and whose value can be obtained from the
experimental radiative decay width [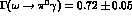 MeV.
MeV. 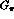 can also be obtained extracting
a value for
can also be obtained extracting
a value for 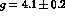 from
from 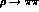 and
and 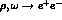 decay data [
decay data [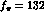 MeV, we then
obtain
MeV, we then
obtain 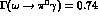 MeV in
good agreement with the experimental result.
In our normalization, the radiative decay widths
for vector mesons are given by
MeV in
good agreement with the experimental result.
In our normalization, the radiative decay widths
for vector mesons are given by
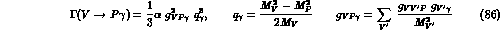
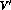 . Thanks to this, one immediately recovers the
successful relation (
. Thanks to this, one immediately recovers the
successful relation (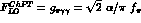 ,
coming from the WZ anomaly and satisfied by the experimental
,
coming from the WZ anomaly and satisfied by the experimental
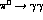 decay rate.
decay rate.
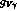 are easily
obtained from the lagrangian in eq.(
are easily
obtained from the lagrangian in eq.(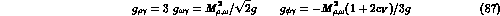
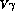 couplings with all equal masses (
couplings with all equal masses (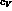 such that
such that
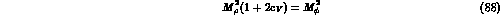
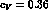 ,
not far from the range of values
for which a good fit to a large number of
other low energy constant was obtained in the previous section.
With this choice, we then have
,
not far from the range of values
for which a good fit to a large number of
other low energy constant was obtained in the previous section.
With this choice, we then have
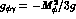 and using eqs.(
and using eqs.(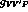 couplings, we obtain the
following expressions for the coupling constants
couplings, we obtain the
following expressions for the coupling constants 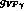
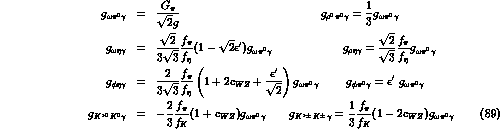
 is the one introduced in section 4,
eq.(
is the one introduced in section 4,
eq.( (
( ) meson.
Notice that, because of eq.(
) meson.
Notice that, because of eq.( disappears from the above relations, which now contain only
disappears from the above relations, which now contain only
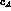 and
and 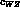 . The value of the anomalous breaking
parameter
. The value of the anomalous breaking
parameter
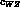 can be directly obtained
from the ratio between the experimental decay widths [
can be directly obtained
from the ratio between the experimental decay widths [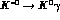 and
and 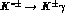 .
The ratio depends only from
.
The ratio depends only from 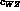 and leads immediately to
and leads immediately to
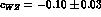 , whereas for
, whereas for 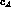 we can use eq.(
we can use eq.(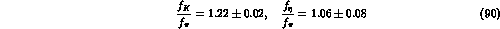
 as obtained in the previous
section.
as obtained in the previous
section.
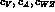 can be put to a test by calculating
the V radiative decay widths
following eq.(
can be put to a test by calculating
the V radiative decay widths
following eq.(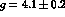 and
and
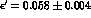 , as well as
, as well as 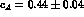 and
and
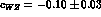 for the symmetry breaking parameters, are shown
in Table
for the symmetry breaking parameters, are shown
in Table 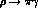 case we have averaged for
neutral and charged decays).
The description of all these data turns out to be quite satisfactory,
with SU(3)-breaking effects playing a central role in some cases. As
already noted by Hajuj [
case we have averaged for
neutral and charged decays).
The description of all these data turns out to be quite satisfactory,
with SU(3)-breaking effects playing a central role in some cases. As
already noted by Hajuj [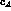 (thus achieving
(thus achieving 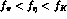 ) is essential to
reduce the predicted
) is essential to
reduce the predicted 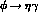 and
and 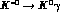 decay rates to their experimental values. Our value
decay rates to their experimental values. Our value 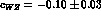 is also crucial to improve the results of ref.[
is also crucial to improve the results of ref.[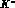 radiative decays) where such a source of
SU(3)-breaking has been neglected. As mentioned, the other SU(3)-breaking
parameter
radiative decays) where such a source of
SU(3)-breaking has been neglected. As mentioned, the other SU(3)-breaking
parameter 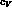 is fixed here so as to satisfy the relation
is fixed here so as to satisfy the relation
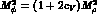 .
.
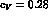 and
and  , which was
considered optimal in the previous section, when chiral
loop
contributions were added to the vector meson terms.
Notice that because the use of eq.(
, which was
considered optimal in the previous section, when chiral
loop
contributions were added to the vector meson terms.
Notice that because the use of eq.(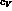 , we refrain
from using it in the whole set of those equations,
which now come to depends explicitly
upon the parameter
, we refrain
from using it in the whole set of those equations,
which now come to depends explicitly
upon the parameter 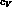 . On its turn, this
means that the whole numerical dependence of those equations upon
the parameters
. On its turn, this
means that the whole numerical dependence of those equations upon
the parameters 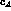 and
and 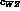 changes and we
obtain a different set of optimal values, which are
in line with the results of refs. [
changes and we
obtain a different set of optimal values, which are
in line with the results of refs. [
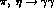 decays,
are accurately described, improving
the results of previous related work [
decays,
are accurately described, improving
the results of previous related work [