


Next: 9 Conclusions
Up: Chapter 1 Section 4
Previous: 7 C-even background
Research in the theory of quantum gravity
[14] led to a proposal
for a modification of quantum mechanics time evolution, which might
transform a pure initial state into an incoherent mixture
[16]. This
effect becomes particularly interesting in the kaon system, where
quantum oscillations can be accurately measured. Moreover the
 -factory, where the initial
-factory, where the initial 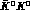 is an antisymmetric coherent state, is a very suitable facility to
test this idea.
We will not discuss the theoretical models of quantum mechanics
violations, which are discussed elsewhere in this handbook
[40],
but, following the analysis of Ref. [18], we
shall analyze some examples of observable effects at DA
is an antisymmetric coherent state, is a very suitable facility to
test this idea.
We will not discuss the theoretical models of quantum mechanics
violations, which are discussed elsewhere in this handbook
[40],
but, following the analysis of Ref. [18], we
shall analyze some examples of observable effects at DA NE .
NE .
To describe the time evolution to incoherent states, one has to introduce
the formalism of the density matrix. In Ref. [16] it has been
proposed to modify the quantum mechanics time evolution
equation in the following way:
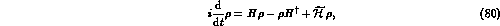
where 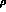 is the
is the 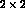 kaon density matrix,
kaon density matrix, 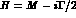 is the
usual non-Hermitian kaon Hamiltonian (see eq. (18))
and
is the
usual non-Hermitian kaon Hamiltonian (see eq. (18))
and 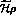 is
the quantum mechanics violating
term. For
is
the quantum mechanics violating
term. For 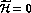 the eigenmatrices of eq. (80) are
the usual matrices:
the eigenmatrices of eq. (80) are
the usual matrices:
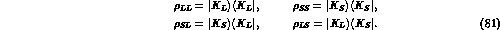
Under reasonable assumptions (probability conservation,
not decreasing entropy and strangeness conservation)
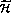 can be expressed in terms of the three real parameters
can be expressed in terms of the three real parameters
 ,
,  and
and 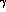 of Ref. [16]. With this
parametrization the new eigenmatrices become:
of Ref. [16]. With this
parametrization the new eigenmatrices become:
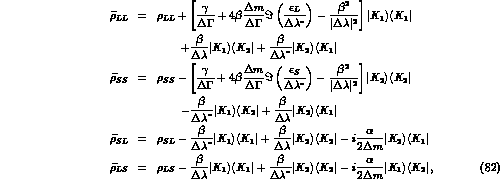
where 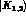 are the usual CP eigenstates and
are the usual CP eigenstates and
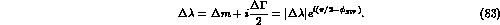
The analysis of fixed target experiments has led
the authors of Ref. [18] to
put stringent bounds on the quantum mechanics
violating parameters  and
and 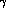 :
:
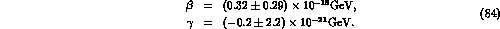
Quite similar results were already obtained in [17]. In
[41] also a
bound for  (
(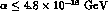 ) is derived.
It is interesting to note that, using the values in eq. (84),
the limits on
) is derived.
It is interesting to note that, using the values in eq. (84),
the limits on 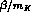 and
and 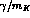 turn out to be of the order of
turn out to be of the order of
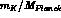 , which could be the natural suppression factor for
these parameters.
, which could be the natural suppression factor for
these parameters.
These limits have been obtained assuming that there is no CPT
violation in the decay amplitudes. In the more general case
the effects of  ,
, 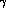 and those of
the conventional CPT-violating terms are mixed together.
and those of
the conventional CPT-violating terms are mixed together.
This situation could be improved at DA NE . In effect,
quantum mechanics predicts a vanishing
amplitude for the transition to the final state
NE . In effect,
quantum mechanics predicts a vanishing
amplitude for the transition to the final state 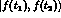 ,
with
,
with 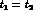 , independently from possible CPT violations.
Therefore, as pointed out in
[18], any measurement of equal time
, independently from possible CPT violations.
Therefore, as pointed out in
[18], any measurement of equal time 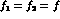 events can give
a bound for pure quantum mechanics violations.
It should be stressed however that
the finite experimental resolution will partially wash out these effects
(see Fig. 2). Moreover, also the C-even background gives rise to equal time
events.
Thus only the time distribution, which is different for
C-even background and quantum mechanics violations,
could help in disentangling them.
events can give
a bound for pure quantum mechanics violations.
It should be stressed however that
the finite experimental resolution will partially wash out these effects
(see Fig. 2). Moreover, also the C-even background gives rise to equal time
events.
Thus only the time distribution, which is different for
C-even background and quantum mechanics violations,
could help in disentangling them.
In Ref. [18] the consequences of quantum mechanics violation
to several DA NE \
observables have been analyzed. In particular the explicit formula
of the
NE \
observables have been analyzed. In particular the explicit formula
of the 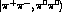 time difference distribution
has been derived, discussing the quantum mechanics violating effects in the
measurement of
time difference distribution
has been derived, discussing the quantum mechanics violating effects in the
measurement of 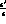 . For
. For 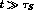 the time asymmetry of
eq. (11) becomes:
the time asymmetry of
eq. (11) becomes:
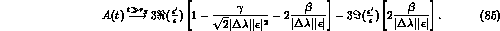
In Fig. 7 we have plotted
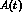 in the usual quantum mechanics case
and in the quantum mechanics violating case (following the
analysis of [18]), for
in the usual quantum mechanics case
and in the quantum mechanics violating case (following the
analysis of [18]), for 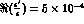 and
and
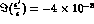 , 0 and
, 0 and 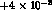 (close to the predicted DA
(close to the predicted DA NE
sensitivity). The quantum mechanics violating parameters have been chosen to be:
NE
sensitivity). The quantum mechanics violating parameters have been chosen to be:
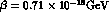 and
and 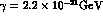 , in order to maximize their effects.
As one can see, for very small values of the time difference
t the effects of quantum mechanics violations are striking,
but probably beyond any realistic experimental resolution.
The determination of
, in order to maximize their effects.
As one can see, for very small values of the time difference
t the effects of quantum mechanics violations are striking,
but probably beyond any realistic experimental resolution.
The determination of 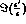 should not be affected, but
an effect could be present in the asymptotic value of
the asymmetry where, contrary to the usual quantum mechanics case,
also
should not be affected, but
an effect could be present in the asymptotic value of
the asymmetry where, contrary to the usual quantum mechanics case,
also 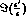 contributes.
contributes.
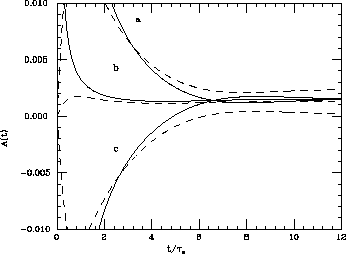
Figure 7: The time asymmetry 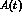 for
for 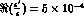 .
The full lines correspond to quantum
mechanics predictions of eqs. (11) and (12),
with
.
The full lines correspond to quantum
mechanics predictions of eqs. (11) and (12),
with 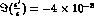 (a), 0 (b) and
(a), 0 (b) and
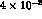 (c).
The dashed lines correspond to
the upper bounds of quantum mechanics
violating parameters
(c).
The dashed lines correspond to
the upper bounds of quantum mechanics
violating parameters 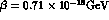 and
and 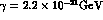 ,
for the previous values of
,
for the previous values of 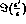 .
.
Using the expressions of Ref. [18] and neglecting a
possible violation of the 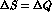 rule, we have calculated
also the quantum mechanics violating effects for eq. (25).
The measured charge asymmetry for
rule, we have calculated
also the quantum mechanics violating effects for eq. (25).
The measured charge asymmetry for 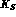 semileptonic decays would become:
semileptonic decays would become:
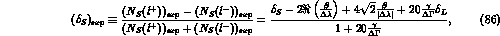
where 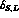 are the usual asymmetries, as defined in
eq. (23). The effect of the
are the usual asymmetries, as defined in
eq. (23). The effect of the 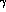 term simulates
a C-even background and interestingly, with the
limit of eq. (84), this correction turns out to be
of the order of the one estimated in the previous section
(for
term simulates
a C-even background and interestingly, with the
limit of eq. (84), this correction turns out to be
of the order of the one estimated in the previous section
(for 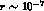 ). The
). The  term
simulates a CPT violation, however, using
the bound in eq. (84), this effect turns out to be
smaller than the DA
term
simulates a CPT violation, however, using
the bound in eq. (84), this effect turns out to be
smaller than the DA NE sensitivity.
NE sensitivity.
Concluding, we can say that quantum mechanics violating effects can be
neglected in integrated asymmetries at DA NE . Nevertheless,
if
NE . Nevertheless,
if  ,
,  and
and 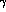 were suppressed only linearly by
were suppressed only linearly by
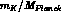 , some
effects in time-dependent distributions could be observable.
An estimate of DA
, some
effects in time-dependent distributions could be observable.
An estimate of DA NE sensitivity on these effects
would require an accurate simulation of the experimental apparatus,
which is beyond the purpose of this work.
NE sensitivity on these effects
would require an accurate simulation of the experimental apparatus,
which is beyond the purpose of this work.



Next: 9 Conclusions
Up: Chapter 1 Section 4
Previous: 7 C-even background
Carlos E.Piedrafita
 -factory, where the initial
-factory, where the initial 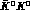 is an antisymmetric coherent state, is a very suitable facility to
test this idea.
We will not discuss the theoretical models of quantum mechanics
violations, which are discussed elsewhere in this handbook
[40],
but, following the analysis of Ref. [18], we
shall analyze some examples of observable effects at DA
is an antisymmetric coherent state, is a very suitable facility to
test this idea.
We will not discuss the theoretical models of quantum mechanics
violations, which are discussed elsewhere in this handbook
[40],
but, following the analysis of Ref. [18], we
shall analyze some examples of observable effects at DA NE .
NE . 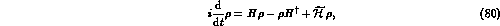
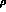 is the
is the 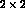 kaon density matrix,
kaon density matrix, 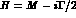 is the
usual non-Hermitian kaon Hamiltonian (see eq. (18))
and
is the
usual non-Hermitian kaon Hamiltonian (see eq. (18))
and 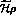 is
the quantum mechanics violating
term. For
is
the quantum mechanics violating
term. For 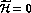 the eigenmatrices of eq. (
the eigenmatrices of eq. (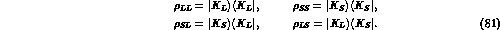
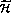 can be expressed in terms of the three real parameters
can be expressed in terms of the three real parameters
 ,
,  and
and 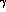 of Ref. [
of Ref. [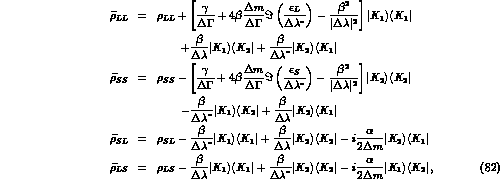
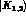 are the usual CP eigenstates and
are the usual CP eigenstates and
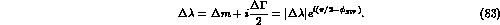
 and
and 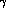 :
:
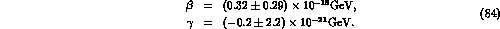
 (
(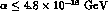 ) is derived.
It is interesting to note that, using the values in eq. (
) is derived.
It is interesting to note that, using the values in eq. (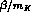 and
and 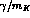 turn out to be of the order of
turn out to be of the order of
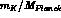 , which could be the natural suppression factor for
these parameters.
, which could be the natural suppression factor for
these parameters.
 ,
, 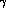 and those of
the conventional CPT-violating terms are mixed together.
and those of
the conventional CPT-violating terms are mixed together.
 NE . In effect,
quantum mechanics predicts a vanishing
amplitude for the transition to the final state
NE . In effect,
quantum mechanics predicts a vanishing
amplitude for the transition to the final state 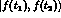 ,
with
,
with 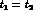 , independently from possible CPT violations.
Therefore, as pointed out in
[
, independently from possible CPT violations.
Therefore, as pointed out in
[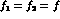 events can give
a bound for pure quantum mechanics violations.
It should be stressed however that
the finite experimental resolution will partially wash out these effects
(see Fig. 2). Moreover, also the C-even background gives rise to equal time
events.
Thus only the time distribution, which is different for
C-even background and quantum mechanics violations,
could help in disentangling them.
events can give
a bound for pure quantum mechanics violations.
It should be stressed however that
the finite experimental resolution will partially wash out these effects
(see Fig. 2). Moreover, also the C-even background gives rise to equal time
events.
Thus only the time distribution, which is different for
C-even background and quantum mechanics violations,
could help in disentangling them.
 NE \
observables have been analyzed. In particular the explicit formula
of the
NE \
observables have been analyzed. In particular the explicit formula
of the 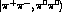 time difference distribution
has been derived, discussing the quantum mechanics violating effects in the
measurement of
time difference distribution
has been derived, discussing the quantum mechanics violating effects in the
measurement of 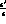 . For
. For 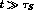 the time asymmetry of
eq. (
the time asymmetry of
eq. (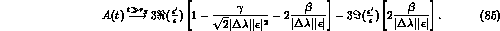
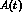 in the usual quantum mechanics case
and in the quantum mechanics violating case (following the
analysis of [
in the usual quantum mechanics case
and in the quantum mechanics violating case (following the
analysis of [ and
and
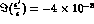 , 0 and
, 0 and 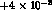 (close to the predicted DA
(close to the predicted DA NE
sensitivity). The quantum mechanics violating parameters have been chosen to be:
NE
sensitivity). The quantum mechanics violating parameters have been chosen to be:
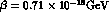 and
and 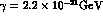 , in order to maximize their effects.
As one can see, for very small values of the time difference
t the effects of quantum mechanics violations are striking,
but probably beyond any realistic experimental resolution.
The determination of
, in order to maximize their effects.
As one can see, for very small values of the time difference
t the effects of quantum mechanics violations are striking,
but probably beyond any realistic experimental resolution.
The determination of 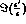 should not be affected, but
an effect could be present in the asymptotic value of
the asymmetry where, contrary to the usual quantum mechanics case,
also
should not be affected, but
an effect could be present in the asymptotic value of
the asymmetry where, contrary to the usual quantum mechanics case,
also 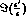 contributes.
contributes.

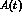 for
for 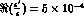 .
The full lines correspond to quantum
mechanics predictions of eqs. (11) and (12),
with
.
The full lines correspond to quantum
mechanics predictions of eqs. (11) and (12),
with 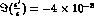 (a), 0 (b) and
(a), 0 (b) and
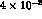 (c).
The dashed lines correspond to
the upper bounds of quantum mechanics
violating parameters
(c).
The dashed lines correspond to
the upper bounds of quantum mechanics
violating parameters 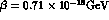 and
and 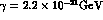 ,
for the previous values of
,
for the previous values of 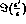 .
.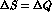 rule, we have calculated
also the quantum mechanics violating effects for eq. (
rule, we have calculated
also the quantum mechanics violating effects for eq. (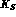 semileptonic decays would become:
semileptonic decays would become:
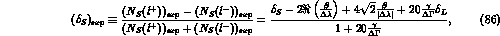
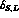 are the usual asymmetries, as defined in
eq. (
are the usual asymmetries, as defined in
eq. (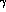 term simulates
a C-even background and interestingly, with the
limit of eq. (
term simulates
a C-even background and interestingly, with the
limit of eq. (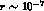 ). The
). The  term
simulates a CPT violation, however, using
the bound in eq. (
term
simulates a CPT violation, however, using
the bound in eq. ( NE sensitivity.
NE sensitivity.
 NE . Nevertheless,
if
NE . Nevertheless,
if  ,
,  and
and 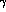 were suppressed only linearly by
were suppressed only linearly by
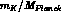 , some
effects in time-dependent distributions could be observable.
An estimate of DA
, some
effects in time-dependent distributions could be observable.
An estimate of DA NE sensitivity on these effects
would require an accurate simulation of the experimental apparatus,
which is beyond the purpose of this work.
NE sensitivity on these effects
would require an accurate simulation of the experimental apparatus,
which is beyond the purpose of this work.