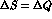We will discuss the semileptonic decays of neutral kaons in a very
general framework, without assuming the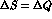 
rule
and the CPT symmetry.
The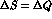 
rule is well supported by experimental
data and is naturally accounted for by the Standard Model, where the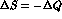 
transitions are possible only with two effective
weak vertices. Explicit
calculations give a suppression factor of about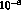 
--
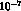[21].
Furthermore in any quark model,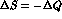 
transitions can be induced only by operators with dimension
higher than 6 and therefore are suppressed [22].
Although it is very unlikely to have a theory with a large violation of
the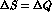 
rule, this does not conflict with any general
principle. On the contrary CPT symmetry
must hold in any Lorentz-invariant local field theory.
The problem of possible sources of CPT violation has recently received
much attention. Attempts to include also gravitation in the unification
of fundamental interactions lead to non-local theories, like superstrings,
which suggest possible CPT violation above the Planck mass, which turns out
to be the natural suppression scale [23].
We neglect for the moment quantum mechanics violating effects [16], which will be discussed later, introducing CPT violation through an ``ad hoc" parametrization of the decay amplitudes and the mass matrix elements.
Following the notations of Ref. [22] we define:
CPT implies b=d=0, CP implies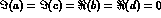 
,
T requires real amplitudes and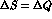 
implies c=d=0.
Writing the mass matrix for the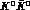 
system in the form:
the eigenstates are given by:
where the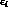 
parameters are:
Then the masses and widths are:
CPT symmetry would require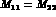 
and
, recovering the relation
.
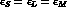Using eqs. (17) and (19) the semileptonic partial rates are given by:
thus the charge asymmetries for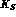 
and 
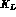are:
A non-vanishing value of the
difference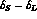 
would be an evidence of
CPT violation, either in the
mass matrix or in the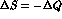 
amplitudes (
and
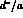cannot be disentangled by semileptonic decays alone).
The sum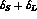 
has CPT-conserving (
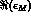) and
CPT-violating (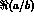
) contributions that cannot be disentangled.
The ratio of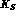 
and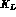 
semileptonic widths
where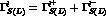 
,
allows us to determine the
CPT-conserving part of the amplitudes with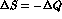 
.
All imaginary parts disappear from the rates and only the time evolution can potentially give some information on them.
