 factory is very
suitable for an accurate study of the origin of CP violation in
factory is very
suitable for an accurate study of the origin of CP violation in 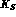 and
and
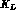 decays and to test the Standard Model predictions.
decays and to test the Standard Model predictions.
From the previous analysis it is clear that a  factory is very
suitable for an accurate study of the origin of CP violation in
factory is very
suitable for an accurate study of the origin of CP violation in 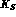 and
and
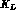 decays and to test the Standard Model predictions.
decays and to test the Standard Model predictions.
The real part of the ratio 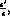 which is a clear signal of direct CP violation,
can be measured with high precision, about
which is a clear signal of direct CP violation,
can be measured with high precision, about 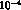 . A non-vanishing value
of the imaginary part of
. A non-vanishing value
of the imaginary part of 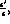 which would imply CPT violation, can be
detected up to some units in
which would imply CPT violation, can be
detected up to some units in 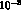 . Even if the fixed target experiments
will reach a similar sensitivity, the KLOE apparatus has a completely
different systematics and such experimental result will be very important.
. Even if the fixed target experiments
will reach a similar sensitivity, the KLOE apparatus has a completely
different systematics and such experimental result will be very important.
The presence of a pure 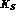 beam will allow, for the first time, the direct
detection of CP violation in
beam will allow, for the first time, the direct
detection of CP violation in 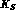 decays. Moreover many interesting tests
of T and CPT symmetries (in addition to
decays. Moreover many interesting tests
of T and CPT symmetries (in addition to 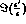 ) can be performed.
) can be performed.
The combined analysis of DA NE , CPLEAR, E731 and NA31 experiments will
allow to disentangle the CPT-violating contributions in decay amplitudes
from those in mass matrix and also the
NE , CPLEAR, E731 and NA31 experiments will
allow to disentangle the CPT-violating contributions in decay amplitudes
from those in mass matrix and also the 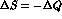 transitions
can be singled out. All the real parts of the
parameters could be bounded up to
transitions
can be singled out. All the real parts of the
parameters could be bounded up to 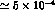 while a lower sensitivity (
while a lower sensitivity (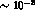 --
--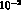 )
is expected for the imaginary parts.
)
is expected for the imaginary parts.
More doubtful is the situation for 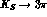 decays. We think
that the CP-conserving decays will certainly be measured and some
information on the rescattering phases could be obtained. For the
CP-violating ones we observe, without doing a complete statistical analysis,
that the shape of the interference effect of Fig. 4 is very
characteristic and could easily be detected over a flat background.
The analysis of the possibility to measure
decays. We think
that the CP-conserving decays will certainly be measured and some
information on the rescattering phases could be obtained. For the
CP-violating ones we observe, without doing a complete statistical analysis,
that the shape of the interference effect of Fig. 4 is very
characteristic and could easily be detected over a flat background.
The analysis of the possibility to measure 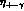 leads to
similar conclusions.
leads to
similar conclusions.
Also the recent suggestions on possible quantum mechanics
violations might be tested at DA NE .
NE .
1.0 true cm
The KLOE detector measures the positions 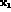 and
and
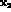 of the two decay vertices. To compare the theoretical
expressions of time dependent
asymmetries with the experimental distributions,
the decay times
of the two decay vertices. To compare the theoretical
expressions of time dependent
asymmetries with the experimental distributions,
the decay times 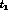 and
and 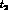 introduced in the
text
introduced in the
text![]() must be transformed to the corresponding decay distances.
Usually this was simply done by using the classical
equations of motion, i.e. through the identity
must be transformed to the corresponding decay distances.
Usually this was simply done by using the classical
equations of motion, i.e. through the identity

where  is the mean velocity of
the two kaons and
is the mean velocity of
the two kaons and 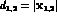 . This
leads to the replacement
. This
leads to the replacement
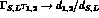 ,
as in [20].
,
as in [20].
Recently, the possibility that the different classical
velocities of 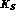 and
and 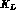 could modify Eq. (A.1) has been suggested in
Ref. [42]. However, such conclusion seems to follow from an incomplete
account of the particle quantum properties, which ultimately overlooks the
distinction between the possible values of
a quantum observable and the corresponding classical value.
Indeed, we present here the proof of Eq. (A.1) based on the description
of the
could modify Eq. (A.1) has been suggested in
Ref. [42]. However, such conclusion seems to follow from an incomplete
account of the particle quantum properties, which ultimately overlooks the
distinction between the possible values of
a quantum observable and the corresponding classical value.
Indeed, we present here the proof of Eq. (A.1) based on the description
of the 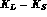 state, in terms of localized
wave-packets, of Ref. [43].
state, in terms of localized
wave-packets, of Ref. [43].![]()
The plane wave state 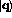 of eq. (1),
is replaced with a wave packet
peaked at
of eq. (1),
is replaced with a wave packet
peaked at 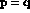 and similarly for
the other state,
and similarly for
the other state, 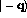 :
:
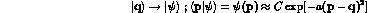
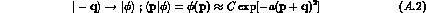
We take, for simplicity, gaussian wave packets, but any other, well-localized, function would give similar results. At time t, one has:
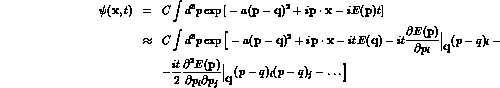
where ellipses represent further terms in the expansion, which can be neglected for a sufficiently narrow packet.
We have to introduce a complex 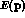 to
describe an unstable particle.
The relativistically invariant propagator for a weakly unstable particle reads:
to
describe an unstable particle.
The relativistically invariant propagator for a weakly unstable particle reads:

from which, at the pole, we derive:
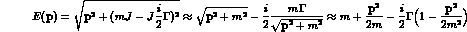
The gaussian integral is easily performed by completing the square, with the result:
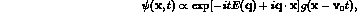
where

g is a gaussian wave-packet with a time-dependent size:
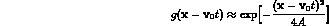

and m is the particle mass. With respect to the stable particle case, there is a contribution to the real part of A from the particle width which, in our case, turns out to be very small.
We consider now the two particle state at time t=0, replacing the plane wave state given in eq. (1) of the text with:
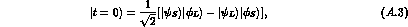
where the subscripts indicate which particle (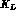 or
or 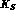 ) is in
which wave packet. At
later times,
the two packets evolve independently, according to the rules given above.
) is in
which wave packet. At
later times,
the two packets evolve independently, according to the rules given above.
The amplitude![]() for a
for a 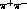 pair to appear at time
pair to appear at time 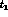 and
location
and
location  , and a
, and a 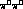 pair at time
pair at time 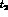 and
location
and
location 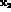 ,
is given by:
,
is given by:
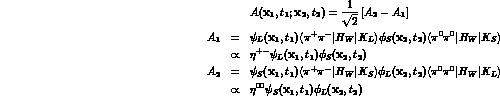
(we are assuming 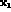 and
and 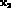 to be on opposite sides of the interaction
region, so that the amplitude that, say, the particle in
to be on opposite sides of the interaction
region, so that the amplitude that, say, the particle in
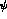 gives rise to an event at
gives rise to an event at
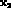 is negligible). According to the previous discussion:
is negligible). According to the previous discussion:
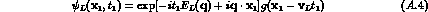
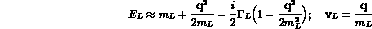
and similarly for the other cases.
Numerically, in the decay 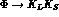 , with
, with  approximately at rest:
approximately at rest:
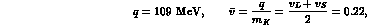
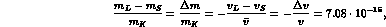
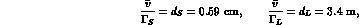
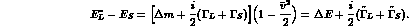
The total number of events (for one initial 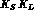 pair)
with the
pair)
with the  pair in
pair in 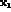 and
the
and
the 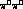 pair in
pair in 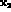 is
found by integrating the probability
over
is
found by integrating the probability
over 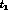 and
and 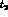 :
:
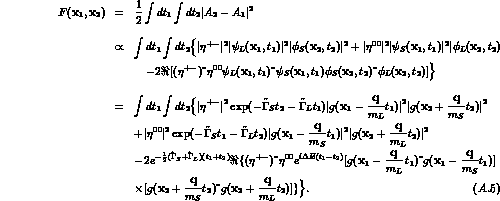
In the direct terms, we may replace each factor 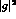 by
a
by
a 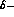 function, thereby obtaining, after integration,
the result of eq. (A.1). In the interference term,
we can do the same, provided
that the difference in the peak position of g and
function, thereby obtaining, after integration,
the result of eq. (A.1). In the interference term,
we can do the same, provided
that the difference in the peak position of g and 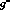 ,
due to the different velocities of
,
due to the different velocities of 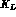 and
and 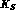 , is
negligible with respect to the width of the wave-packet:
, is
negligible with respect to the width of the wave-packet:

The l.h.s of the inequality is less than a Fermi for 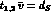 , which is
where the interference term
starts being suppressed by
, which is
where the interference term
starts being suppressed by 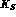 decay. Neglecting the velocity
difference in the interference is thus justified in all the region
of interest, for any reasonable value of the
size
of the wave-packet. Therefore
the total number of events with the
decay. Neglecting the velocity
difference in the interference is thus justified in all the region
of interest, for any reasonable value of the
size
of the wave-packet. Therefore
the total number of events with the 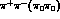 pair at distance
pair at distance 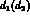 from the interaction vertex
is given by:
from the interaction vertex
is given by:
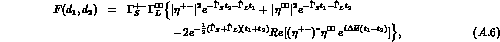
with 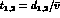 .
.
Considerations leading to analogous results, for the case of single Kaon and B oscillations, have been recently presented in Ref. [44]. A few comments. i) In the case of stable particles, e.g. solar neutrino oscillations, we may reach sufficiently large distances, where the overlap factor:

vanishes. In the far-distant region,
coherent oscillations would disappear to gives rise to
an incoherent superposition of a  and
and  beam.
beam.
ii) the velocity dependent terms in the exponents have reconstructed the correct Lorentz factors. We have obtained exponents of the form:
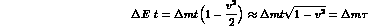
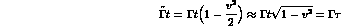
where  is the particle proper time,
as one could have expected on general ground.
is the particle proper time,
as one could have expected on general ground.
iii) One may have preferred to assume exactly
vanishing total momentum, rather then
independently distributed momenta for
the two particles, as done in eq. (A.3). This,
however, is incorrect. A zero- momentum
state is translation invariant. If this were
the case, the intensity 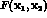 would depend only upon the difference,
would depend only upon the difference,
 , which is obviously wrong.
Electrons and positrons annihilate in the
interaction region and not elsewhere, and
the interaction region is small with respect to
the general dimensions of the experiment. As a
consequence,
, which is obviously wrong.
Electrons and positrons annihilate in the
interaction region and not elsewhere, and
the interaction region is small with respect to
the general dimensions of the experiment. As a
consequence, 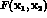 must
depend from the individual distances of the
two points from the interaction region, as in
eq. (A.5).
must
depend from the individual distances of the
two points from the interaction region, as in
eq. (A.5).
Clearly, the initial wave packet
may be not in the factorized form
of eq. (A.3), generally will be a superposition of
all the possible factorized forms (one possibility is
to factorize the c.m. and the relative motion).
However an explicit calculation shows that the result
of eq. (A.6) holds for any form of the initial state, provided it
satisfies the physical constraints: 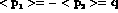 and it
has reasonable widths. Should the result
depend on more particular assumptions, the outcome experiment
would be entirely unpredictable.
and it
has reasonable widths. Should the result
depend on more particular assumptions, the outcome experiment
would be entirely unpredictable.