


Next: 8 Quantum mechanics violations
Up: Chapter 1 Section 4
Previous: 6 Interference in
Some years ago it was pointed out that the radiative  decay
(
decay
(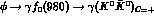 )
could have a non-negligible branching ratio and therefore
could spoil the power of a
)
could have a non-negligible branching ratio and therefore
could spoil the power of a  factory in measuring
factory in measuring 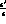 and to single out the suppressed
and to single out the suppressed 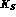 decays [12].
More recent determinations of the resonant contribution consider also the
decays [12].
More recent determinations of the resonant contribution consider also the
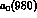 ,
, 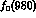 interference effect and
give a much lower value: the ratio
interference effect and
give a much lower value: the ratio
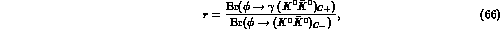
is estimated to be in the range
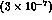 --
--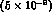 [13].
[13].
These predictions are strongly
model-dependent and larger values could perhaps be obtained; however we can
trust that r is certainly smaller than 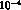 .
The non-resonant contribution to
.
The non-resonant contribution to 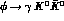 has been evaluated in the current algebra framework [38] to be
of the order of
has been evaluated in the current algebra framework [38] to be
of the order of 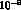 , comparable to the lower
predictions of [13].
As we will show, the effects of the
C-even background on the DA
, comparable to the lower
predictions of [13].
As we will show, the effects of the
C-even background on the DA NE measurements
are negligible also for unrealistically large values of r.
NE measurements
are negligible also for unrealistically large values of r.
The C-even 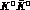 state can be written as:
state can be written as:
where terms of order  have been neglected but the
effect of possible CPT violation has been included.
have been neglected but the
effect of possible CPT violation has been included.
The  component has a CP-conserving decay into the
component has a CP-conserving decay into the  final states and could be a dangerous background in the
final states and could be a dangerous background in the  measurement.
However, the time difference distribution of
these events,
measurement.
However, the time difference distribution of
these events,
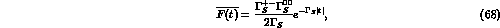
is symmetric and cannot simulate the effect of  .
Furthermore, it vanishes very rapidly for large values of |t|, and
therefore
it does not affect
the determination of
.
Furthermore, it vanishes very rapidly for large values of |t|, and
therefore
it does not affect
the determination of 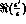 . In effect,
as shown in [39], by means of a suitable cut the background
contribution can be eliminated in the
event sample used to determine
. In effect,
as shown in [39], by means of a suitable cut the background
contribution can be eliminated in the
event sample used to determine 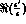 , also for very large values of r.
, also for very large values of r.
The background contribution overlaps the signal just in the
interference zone,
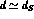 , worsening the resolution on
, worsening the resolution on 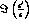 .
However the signal (
.
However the signal (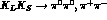 )
and the background
(
)
and the background
(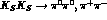 ) have different
spatial behaviour, which is of help
in disentangling the signal contribution from the
background.
The C-even background has been added to the signal in the
fitting procedure of [20] and the accuracy achievable on
) have different
spatial behaviour, which is of help
in disentangling the signal contribution from the
background.
The C-even background has been added to the signal in the
fitting procedure of [20] and the accuracy achievable on
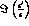 has been estimated again.
The result is that for a realistic vertex
resolution the worsening is around 5%, even if r would be as large
as
has been estimated again.
The result is that for a realistic vertex
resolution the worsening is around 5%, even if r would be as large
as 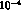 .
.
The 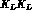 component can affect the determination of the suppressed
component can affect the determination of the suppressed
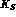 branching ratios and the corresponding CP-violating asymmetries, as
we will discuss in the following.
branching ratios and the corresponding CP-violating asymmetries, as
we will discuss in the following.
If the 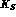 semileptonic decays are
tagged as in eq. (25), the number of events generated by
a single C-even
semileptonic decays are
tagged as in eq. (25), the number of events generated by
a single C-even 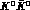 pair is:
pair is:
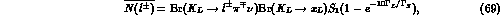
then eq. (27) is modified in:
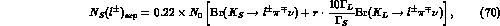
and the measured charge asymmetry becomes:
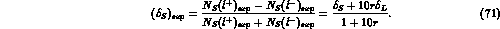
As can be seen the correction is absolutely negligible and cannot
simulate CPT violation, in fact 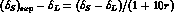 .
.
The number of equal-sign dilepton events generated by
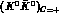 is:
is:
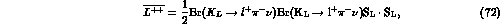
and that of opposite sign is:
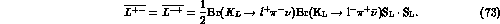
Therefore the experimentally measured T- and CPT-violating asymmetries are:
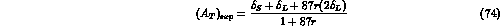
and
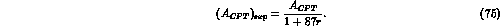
Also in this case the effect of the C-even background is negligible
and the CPT prediction 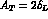 is still valid.
is still valid.
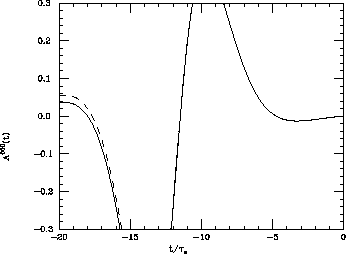
Figure 6: The effect of the C-even background on 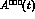 . The full
line corresponds to r = 0 and the dashed one to
. The full
line corresponds to r = 0 and the dashed one to 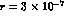 .
.
Finally we discuss the effect of C-even background in 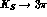 decays, where the largest influence is expected.
decays, where the largest influence is expected.
The inclusion of the background contribution in eq. (49) gives:
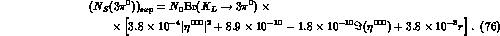
Therefore, for 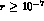 the background is comparable to the signal,
enforcing the conclusion that the direct tag of the
the background is comparable to the signal,
enforcing the conclusion that the direct tag of the 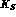 is
not useful to determine Br(
is
not useful to determine Br(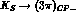 ).
On the contrary, if the
).
On the contrary, if the 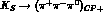 branching ratio is
branching ratio is 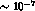 , in agreement with ChPT predictions
and preliminary CPLEAR results,
the background contribution to this decay
can be neglected and the corresponding branching ratio can be measured.
, in agreement with ChPT predictions
and preliminary CPLEAR results,
the background contribution to this decay
can be neglected and the corresponding branching ratio can be measured.
The modifications induced in interference measurements require a more
detailed study.
The analogue of the time difference distribution defined in eq. (8)
for an initial 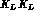 state is
state is
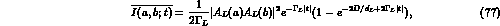
where the last factor accounts for having both 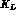 decays inside the detector.
Thus the C-even background, which is symmetric in
decays inside the detector.
Thus the C-even background, which is symmetric in 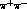 momenta, modifies eqs. (51, 52) in the following way:
momenta, modifies eqs. (51, 52) in the following way:
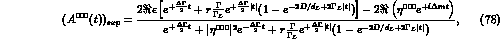
and
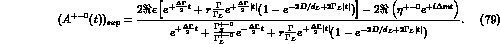
The contribution of the C-even background becomes important (especially in the
numerator) for large and negative values of the time difference,
where the number of events is absolutely negligible,
but, as can be seen from Fig. 6,
does not affect the results for
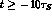 .
.
In the CP-conserving ratio 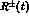 the C-even background
contributes in the denominator only and can be safely neglected.
the C-even background
contributes in the denominator only and can be safely neglected.



Next: 8 Quantum mechanics violations
Up: Chapter 1 Section 4
Previous: 6 Interference in
Carlos E.Piedrafita
 decay
(
decay
(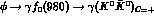 )
could have a non-negligible branching ratio and therefore
could spoil the power of a
)
could have a non-negligible branching ratio and therefore
could spoil the power of a  factory in measuring
factory in measuring 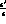 and to single out the suppressed
and to single out the suppressed 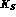 decays [12].
More recent determinations of the resonant contribution consider also the
decays [12].
More recent determinations of the resonant contribution consider also the
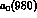 ,
, 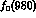 interference effect and
give a much lower value: the ratio
interference effect and
give a much lower value: the ratio
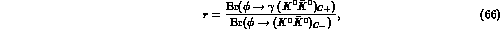
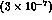 --
--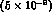 [
[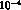 .
The non-resonant contribution to
.
The non-resonant contribution to 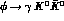 has been evaluated in the current algebra framework [
has been evaluated in the current algebra framework [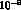 , comparable to the lower
predictions of [
, comparable to the lower
predictions of [ NE measurements
are negligible also for unrealistically large values of r.
NE measurements
are negligible also for unrealistically large values of r.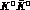 state can be written as:
state can be written as:
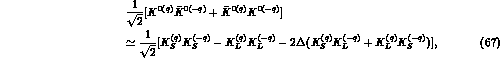
 have been neglected but the
effect of possible CPT violation has been included.
have been neglected but the
effect of possible CPT violation has been included.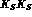 component has a CP-conserving decay into the
component has a CP-conserving decay into the  final states and could be a dangerous background in the
final states and could be a dangerous background in the 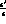 measurement.
However, the time difference distribution of
these events,
measurement.
However, the time difference distribution of
these events,
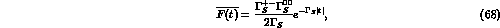
 .
Furthermore, it vanishes very rapidly for large values of |t|, and
therefore
it does not affect
the determination of
.
Furthermore, it vanishes very rapidly for large values of |t|, and
therefore
it does not affect
the determination of 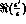 . In effect,
as shown in [
. In effect,
as shown in [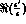 , also for very large values of r.
, also for very large values of r.
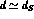 , worsening the resolution on
, worsening the resolution on 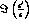 .
However the signal (
.
However the signal (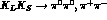 )
and the background
(
)
and the background
(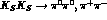 ) have different
spatial behaviour, which is of help
in disentangling the signal contribution from the
background.
The C-even background has been added to the signal in the
fitting procedure of [
) have different
spatial behaviour, which is of help
in disentangling the signal contribution from the
background.
The C-even background has been added to the signal in the
fitting procedure of [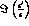 has been estimated again.
The result is that for a realistic vertex
resolution the worsening is around 5%, even if r would be as large
as
has been estimated again.
The result is that for a realistic vertex
resolution the worsening is around 5%, even if r would be as large
as 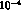 .
.
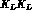 component can affect the determination of the suppressed
component can affect the determination of the suppressed
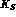 branching ratios and the corresponding CP-violating asymmetries, as
we will discuss in the following.
branching ratios and the corresponding CP-violating asymmetries, as
we will discuss in the following.
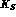 semileptonic decays are
tagged as in eq. (
semileptonic decays are
tagged as in eq. ( pair is:
pair is:
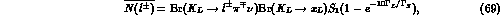
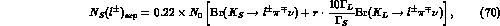
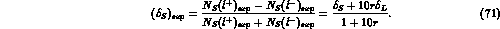
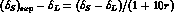 .
. is:
is:
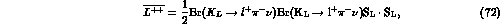
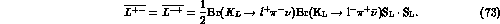
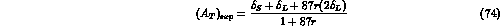
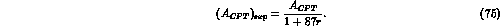
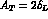 is still valid.
is still valid. 
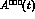 . The full
line corresponds to r = 0 and the dashed one to
. The full
line corresponds to r = 0 and the dashed one to 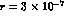 .
. 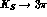 decays, where the largest influence is expected.
decays, where the largest influence is expected.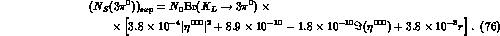
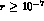 the background is comparable to the signal,
enforcing the conclusion that the direct tag of the
the background is comparable to the signal,
enforcing the conclusion that the direct tag of the 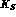 is
not useful to determine Br(
is
not useful to determine Br(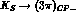 ).
On the contrary, if the
).
On the contrary, if the 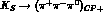 branching ratio is
branching ratio is 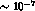 , in agreement with ChPT predictions
and preliminary CPLEAR results,
the background contribution to this decay
can be neglected and the corresponding branching ratio can be measured.
, in agreement with ChPT predictions
and preliminary CPLEAR results,
the background contribution to this decay
can be neglected and the corresponding branching ratio can be measured.
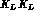 state is
state is
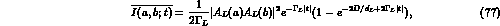
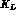 decays inside the detector.
Thus the C-even background, which is symmetric in
decays inside the detector.
Thus the C-even background, which is symmetric in 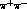 momenta, modifies eqs. (
momenta, modifies eqs. (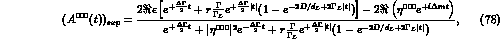
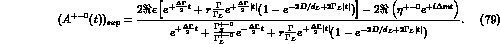
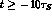 .
.
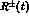 the C-even background
contributes in the denominator only and can be safely neglected.
the C-even background
contributes in the denominator only and can be safely neglected.