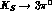 decay is a pure CP-violating transition,
while the
decay is a pure CP-violating transition,
while the 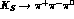 decay receives both CP-conserving and
CP-violating contributions.
decay receives both CP-conserving and
CP-violating contributions.
The 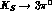 decay is a pure CP-violating transition,
while the
decay is a pure CP-violating transition,
while the 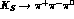 decay receives both CP-conserving and
CP-violating contributions.
decay receives both CP-conserving and
CP-violating contributions.
The CP-conserving 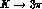 decay amplitudes are well described by
Chiral Perturbation Theory (ChPT). They have been calculated, including
the next-to-leading-order corrections, in Ref. [27] and turn out
to be in good agreement with the experimental data.
The CP-conserving
decay amplitudes are well described by
Chiral Perturbation Theory (ChPT). They have been calculated, including
the next-to-leading-order corrections, in Ref. [27] and turn out
to be in good agreement with the experimental data.
The CP-conserving 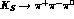 decay amplitude is odd under
decay amplitude is odd under
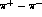 momenta exchange and thus, neglecting final states
with high angular momenta, it is induced by
a
momenta exchange and thus, neglecting final states
with high angular momenta, it is induced by
a 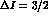 transition. The ChPT calculation of Ref. [27]
leads to the prediction:
transition. The ChPT calculation of Ref. [27]
leads to the prediction:
consistent with the recent data:
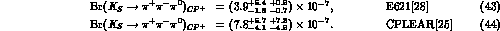
As in 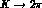 decays, for the CP-violating amplitudes
it is convenient to define the ratios:
decays, for the CP-violating amplitudes
it is convenient to define the ratios:
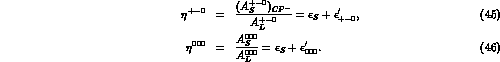
The direct CP-violating parameters 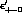 and
and  have been evaluated at lowest order in ChPT [29] and turn out to
be of the same order as
have been evaluated at lowest order in ChPT [29] and turn out to
be of the same order as  . As shown in [30], higher-order terms can substantially enhance
. As shown in [30], higher-order terms can substantially enhance
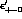 and
and  , which are nevertheless
negligible
, which are nevertheless
negligible![]() compared to
compared to  . The
predicted branching ratios are:
. The
predicted branching ratios are:
much smaller then the present upper limits [24,25,31].
Due to the smallness of the branching ratios
it is very hard to detect 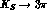 decays, especially the
CP-violating ones. Tagging the
decays, especially the
CP-violating ones. Tagging the 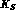 as in the case of the semileptonic
decays (eqs. (25) and (26))
and inserting the numerical values,
one gets for
as in the case of the semileptonic
decays (eqs. (25) and (26))
and inserting the numerical values,
one gets for 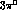 final state:
final state:
The total number of events is very small ( 6 per year)
and the ratio of right events (those with a
6 per year)
and the ratio of right events (those with a 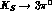 decay)
to wrong ones (those with a
decay)
to wrong ones (those with a 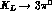 decay)
is only 2.2.
decay)
is only 2.2.
In the case of the CP-conserving 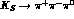 decay,
the expected number of events is about 440 with a negligible
background.
decay,
the expected number of events is about 440 with a negligible
background.
A more promising way to detect the CP-violating
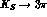 decays is to study the
interference terms of
decays is to study the
interference terms of 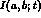 , in eq. (8), choosing
, in eq. (8), choosing
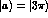 and
and 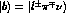 , as
suggested in Refs. [32,33].
For the
, as
suggested in Refs. [32,33].
For the 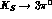 it is useful to define the asymmetry:
it is useful to define the asymmetry:
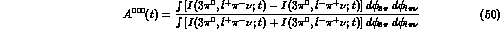
which, integrating over the 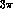 and
and 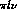 Dalitz plots,
becomes:
Dalitz plots,
becomes:
For positive and large values of the time difference t, eq. (51)
reads: 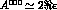 ;
on the other hand, for negative value of t, one gets an interesting
interference effect between
;
on the other hand, for negative value of t, one gets an interesting
interference effect between  and
and 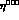 , as shown in Fig. 4.
The asymmetry for t<0 is quite large, but the total number of events
is small, about
, as shown in Fig. 4.
The asymmetry for t<0 is quite large, but the total number of events
is small, about 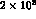 per year.
per year.
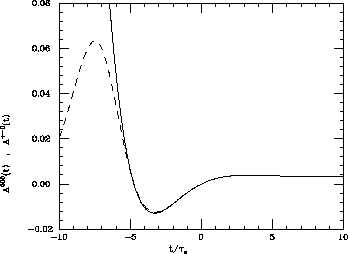
Figure 4: The asymmetries 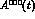 (full line) and
(full line) and 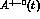 (
dashed line). We have fixed
(
dashed line). We have fixed 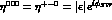 .
.
In the case of the 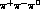 final state, the CP-violating and
CP-conserving amplitudes have opposite symmetry under
final state, the CP-violating and
CP-conserving amplitudes have opposite symmetry under
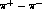 momentum exchange. Therefore it is possible to select
the CP-violating and the CP-conserving part of the interference term in
eq.(8) with an even or an odd integration over the
momentum exchange. Therefore it is possible to select
the CP-violating and the CP-conserving part of the interference term in
eq.(8) with an even or an odd integration over the
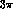 Dalitz plot. Analogously to the
Dalitz plot. Analogously to the 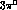 case,
for the CP-violating part we define the asymmetry:
case,
for the CP-violating part we define the asymmetry:
while the CP-conserving part can be singled out by the ratio:
where 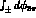 indicates the integration in
the region
indicates the integration in
the region 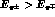 .
.
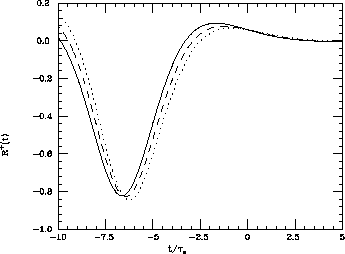
Figure 5: The ratio 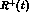 defined in eq.(53).
The full, dashed and dotted
lines correspond to
defined in eq.(53).
The full, dashed and dotted
lines correspond to 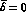 ,
, 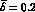 and
and
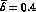 respectively.
respectively.
The behaviour of 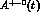 is completely analogous to the one of
is completely analogous to the one of
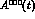 (Fig. 4). As discussed in refs. [32,33]
the study of
(Fig. 4). As discussed in refs. [32,33]
the study of 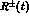 will certainly lead to a determination of the
will certainly lead to a determination of the
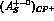 amplitude, performing an interesting test of
ChPT in the
amplitude, performing an interesting test of
ChPT in the 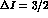 transitions, and perhaps could also lead
to a direct measurement of the
transitions, and perhaps could also lead
to a direct measurement of the 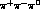 rescattering functions.
The phase
rescattering functions.
The phase  of eq. (53) can be written as:
of eq. (53) can be written as:
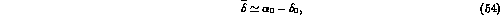
where 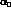 and
and  are the first terms
in the expansion of the
are the first terms
in the expansion of the 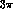 rescattering functions
of the I=2 and of the symmetric I=1 final states, respectively.
The ChPT prediction is
rescattering functions
of the I=2 and of the symmetric I=1 final states, respectively.
The ChPT prediction is 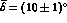 [33]
and the first measurement [28] gives
[33]
and the first measurement [28] gives
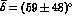 .
With a different integration over the Dalitz plot, also the
rescattering function of the non-symmetric I=1 final state
could be selected [32,33].
Figure 5 shows the behaviour of
.
With a different integration over the Dalitz plot, also the
rescattering function of the non-symmetric I=1 final state
could be selected [32,33].
Figure 5 shows the behaviour of 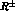 for different values of
for different values of
 .
.