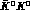The antisymmetric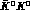 
state
produced in the 
decay can be written as
where 
and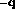 
indicate the spatial momenta of the two-kaons and
the normalization factor h is
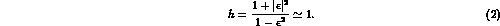
The decay amplitude of the two-kaon system into the final state
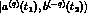is given by:
where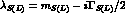 
.
As usual we define also:
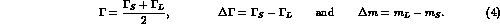
If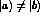 
the two states 
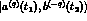and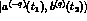 
are physically different for any
value of 
and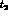 
, therefore the double differential rate is:
where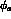 
and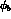 
are the phase spaces of the final states.
Integrating eq. (5) on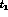 
and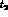 
one obtains
the probability for the decay into the 
state with both the
decay vertices inside the detector:
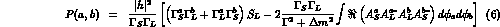
where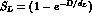 
is the 
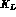acceptance of
the detector: the KLOE project quotes for the fiducial length
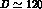cm [3]
(
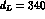cm is the 
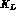mean decay path), thus 
.
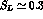For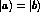 
the interchange of
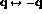is equivalent
to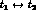 
, thus:
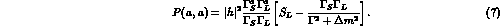
As will be discussed in the following, the choice of appropriate time integration
intervals supplies a powerful tagging of 
or 
decays.
Finally we define also the so-called ``time difference distribution'':
