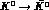 and
and
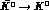 transitions, while CPT requires equal probabilities
for
transitions, while CPT requires equal probabilities
for 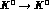 and
and 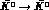 transitions.
Then a T-violating asymmetry:
transitions.
Then a T-violating asymmetry:
The dilepton events allow direct tests of T and CPT symmetries
[2,11].
A long time ago Kabir [26] showed that T violation implies
different probabilities for 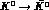 and
and
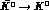 transitions, while CPT requires equal probabilities
for
transitions, while CPT requires equal probabilities
for 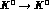 and
and 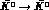 transitions.
Then a T-violating asymmetry:
transitions.
Then a T-violating asymmetry:
and a CPT-violating one:
can be defined.
Both these tests can be done at a  factory, where the initial state
is an antisymmetric
factory, where the initial state
is an antisymmetric 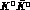 state, if the
state, if the 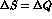 rule
holds.
rule
holds.
If a neutral kaon decays into a positive lepton at a time t, the
other neutral kaon is at the same time a 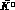 and
the sign of the lepton, emitted
in a subsequent semileptonic decay, signals if the
and
the sign of the lepton, emitted
in a subsequent semileptonic decay, signals if the 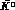 has changed or
conserved its own flavour. Therefore,
if
has changed or
conserved its own flavour. Therefore,
if 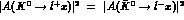 , the charge asymmetry
in equal-sign dilepton pairs measured at the
, the charge asymmetry
in equal-sign dilepton pairs measured at the  factory will be
equal to
factory will be
equal to 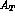 . On the other hand, time asymmetry in opposite-sign
dilepton pairs signals CPT violation.
. On the other hand, time asymmetry in opposite-sign
dilepton pairs signals CPT violation.
In the more general case, taking into account
also possible violations of the 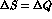 rule
one gets
rule
one gets![]() :
:
and
where 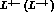 is the number of dilepton pairs
with the positive lepton emitted before (after) the negative one.
The number of equal-sign electron pairs (
is the number of dilepton pairs
with the positive lepton emitted before (after) the negative one.
The number of equal-sign electron pairs (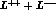 )
and that of opposite-sign (
)
and that of opposite-sign (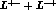 ) expected
at DA
) expected
at DA NE is about
NE is about 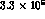 events/year,
therefore the T- and CPT-violating asymmetries can be measured with a statistical error of about
events/year,
therefore the T- and CPT-violating asymmetries can be measured with a statistical error of about
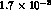 .
.
Violation of the 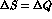 rule does not affect eq. (30)
but the CPT violation in the decay amplitude contributes together with the
true T-violating term
rule does not affect eq. (30)
but the CPT violation in the decay amplitude contributes together with the
true T-violating term 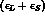 .
On the contrary in eq. (31)
the effects of CPT violation and
.
On the contrary in eq. (31)
the effects of CPT violation and 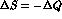 transitions cannot be disentangled.
transitions cannot be disentangled.
In the CPT limit the time asymmetry can be written as:
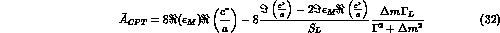
and inserting the experimental limits on 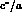 [24] one has:
[24] one has:
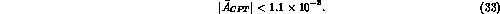
Thus a value of 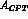 larger than
larger than 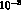 indicates an actual
CPT violation either in the kaon mass matrix or in
indicates an actual
CPT violation either in the kaon mass matrix or in 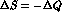 transition amplitudes.
transition amplitudes.
More information can be obtained by
the study of the time dependence of opposite sign dilepton events.
Choosing for the final states of eq. (8)
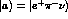 and
and 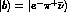 and integrating over the
phase space one gets:
and integrating over the
phase space one gets:
where
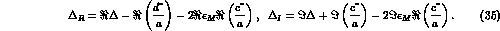
The difference in the asymptotic limits (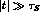 ) leads
to the determination of
) leads
to the determination of 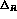 ,
while the interference term singles out
,
while the interference term singles out
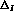 .
The higher-order terms can be neglected (their upper bound is about
.
The higher-order terms can be neglected (their upper bound is about
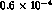 , smaller than the DA
, smaller than the DA NE sensitivity),
but the CPT-violating parameter
NE sensitivity),
but the CPT-violating parameter  and the
and the 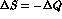 contributions are still mixed.
An exact determination of the statistical error on
contributions are still mixed.
An exact determination of the statistical error on 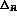 and
and 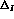 would require a simulation of the experimental apparatus, which is
beyond the purpose of this work. To give an idea of the DA
would require a simulation of the experimental apparatus, which is
beyond the purpose of this work. To give an idea of the DA NE sensitivity
we report in Fig. 3 the asymmetry in opposite-sign dileptons as a function
of the time difference
NE sensitivity
we report in Fig. 3 the asymmetry in opposite-sign dileptons as a function
of the time difference
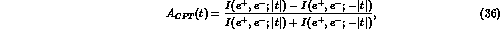
for 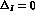 and
and 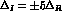 .
As can be seen the asymptotic value is reached very soon and the three
curves are clearly distinct. Therefore we estimate
.
As can be seen the asymptotic value is reached very soon and the three
curves are clearly distinct. Therefore we estimate 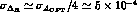 . The value of
. The value of
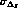 depends critically on the experimental resolution.
We estimate that, as happens for the real and the imaginary parts of
depends critically on the experimental resolution.
We estimate that, as happens for the real and the imaginary parts of 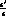 ,
,
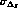 will be about 20 times larger than
will be about 20 times larger than 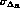 .
.
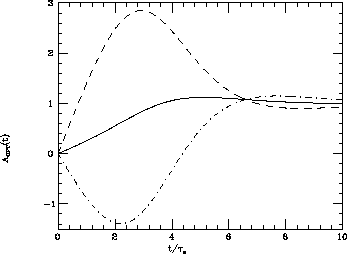
Figure 3: The asymmetry  as a function of the time difference
for
as a function of the time difference
for 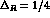 . The full, dashed and dot-dashed lines correspond to
. The full, dashed and dot-dashed lines correspond to
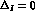 ,
, 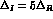 and
and 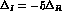 respectively.
respectively.
As shown in Ref. [22], the inclusion in the analysis of
the 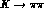 decays allows us to
disentangle almost all the amplitudes. Indeed,
in the Wu-Yang phase convention,
decays allows us to
disentangle almost all the amplitudes. Indeed,
in the Wu-Yang phase convention,![]() unitarity implies that
the phase of
unitarity implies that
the phase of 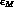 is equal to
is equal to
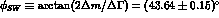 and the phase of
and the phase of 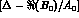 is
is
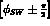 ;
therefore, one has [11,22]:
;
therefore, one has [11,22]:
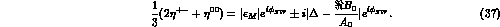
The present experimental data on 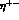 and
and 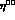 [24]
give:
[24]
give:
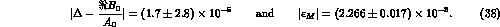
As can be seen, the CPT constraint is at present very well satisfied
and, assuming CPT conservation in decay amplitudes, the limit in 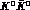 mass difference is
mass difference is
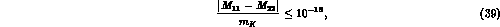
close to the natural scale factor 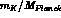 .
.
In addition, from the measured value of 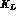 charge asymmetry one gets:
charge asymmetry one gets:
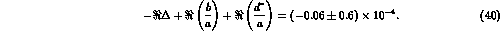
The future measurement of 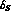 at DA
at DA NE would lead also
to the determination of
NE would lead also
to the determination of 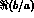 , while the
CPLEAR experiment will give direct measurement
of
, while the
CPLEAR experiment will give direct measurement
of 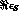 and of
and of 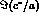 .
Therefore all the parameters that appear in the observables introduced above
can be disentangled, and some consistency relations must be satisfied.
The preliminary data of the CPLEAR collaboration [25]
have large errors and still do not give significant bounds.
We report in Table 2 the relations between the observables and the
theoretical parameters with the corresponding statistical errors
from present and future experiments, together with
the consistency equations and the corresponding sensitivity.
To simplify the notations of the table we define
.
Therefore all the parameters that appear in the observables introduced above
can be disentangled, and some consistency relations must be satisfied.
The preliminary data of the CPLEAR collaboration [25]
have large errors and still do not give significant bounds.
We report in Table 2 the relations between the observables and the
theoretical parameters with the corresponding statistical errors
from present and future experiments, together with
the consistency equations and the corresponding sensitivity.
To simplify the notations of the table we define
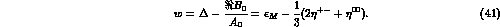
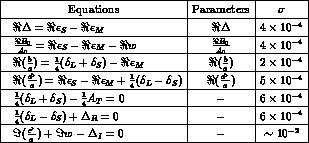
Table 2: Table 2: Statistical errors on parameters and consistency
relations, using
present experimental data
[24] (for 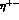 ,
, 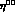 and
and 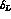 ) together with
DA
) together with
DA NE (for
NE (for 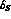 ,
, 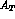 ,
, 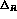 and
and 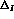 )
and CPLEAR (for
)
and CPLEAR (for 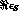 and
and 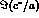 ) future results.
The
) future results.
The  of the last equation in the table is only a guess.
of the last equation in the table is only a guess.