


Next: 6 Measurements at the
Up: 5.2 Factorization and resonance
Previous: 5.2.1 Large calculations
Spin-zero and spin-one resonance exchange, with chiral invariant couplings
between resonances and pseudoscalar mesons, is a phenomenological model which
turns out to be numerically quite successful for the 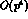 strong
interaction constants. Also, it improves the theoretical description,
by giving a well-recognizable physical meaning to the counterterms. By
construction, this determination of counterterms is
strong
interaction constants. Also, it improves the theoretical description,
by giving a well-recognizable physical meaning to the counterterms. By
construction, this determination of counterterms is  -independent, so
that, in principle, the comparison with the scale-dependent matrix elements of
-independent, so
that, in principle, the comparison with the scale-dependent matrix elements of
 has some ambiguity. Nevertheless, it was shown that
meson exchanges almost entirely saturate those couplings, as being in
good agreement with the values determined phenomenologically from
experimental data in Ref. [21], if the scale
has some ambiguity. Nevertheless, it was shown that
meson exchanges almost entirely saturate those couplings, as being in
good agreement with the values determined phenomenologically from
experimental data in Ref. [21], if the scale 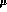 is chosen between,
say,
is chosen between,
say,  and
and 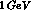 [39,40]. This suggests
that a similar meson-exchange dominance could work also for the weak
constants needed in
[39,40]. This suggests
that a similar meson-exchange dominance could work also for the weak
constants needed in 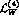 . However, while there exists enough
information to experimentally determine the strong resonance couplings
needed for the
. However, while there exists enough
information to experimentally determine the strong resonance couplings
needed for the 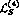 counterterms, in the case of
counterterms, in the case of
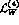 the situation is complicated by the additional need of
weak resonance couplings to pseudoscalar mesons, which are not known
and can only be calculated within specific models. Clearly, as a common
feature, the role of such models is to relate the weak
the situation is complicated by the additional need of
weak resonance couplings to pseudoscalar mesons, which are not known
and can only be calculated within specific models. Clearly, as a common
feature, the role of such models is to relate the weak  constants to
the strong constants, the only ones which are known.
constants to
the strong constants, the only ones which are known.
One possibility is represented by the factorization model previously
introduced, which is based on independent `bosonization' of the weak quark
currents similar to Eq. (36), and leads to a factorized weak
Lagrangian of the form in Eq. (37) (but with with finite 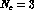 ).
In this case, the strong counterterms needed in the
next-to-leading terms are phenomenologically determined either directly from
experiment or via the resonance exchange parametrization. More
precisely, in the application of Ref. [26], to phenomenologically
account for next-to-leading corrections in
).
In this case, the strong counterterms needed in the
next-to-leading terms are phenomenologically determined either directly from
experiment or via the resonance exchange parametrization. More
precisely, in the application of Ref. [26], to phenomenologically
account for next-to-leading corrections in  a free coefficient
a free coefficient
 is introduced in the factorized expression of
is introduced in the factorized expression of 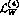 , so
that naive factorization would correspond to
, so
that naive factorization would correspond to  . Another proposed model
is the so-called `weak deformation model' [41], essentially based
on (i) the observation that, at leading order
. Another proposed model
is the so-called `weak deformation model' [41], essentially based
on (i) the observation that, at leading order 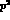 , the weak nonleptonic
Lagrangian can be directly obtained from the strong one by
means of a suitable transformation, called `deformation', and (ii) the
requirement that the same `deformation' generates, more in general, also the
higher order weak Lagrangian from the corresponding strong one. This
model is found to be equivalent to the previous one for
, the weak nonleptonic
Lagrangian can be directly obtained from the strong one by
means of a suitable transformation, called `deformation', and (ii) the
requirement that the same `deformation' generates, more in general, also the
higher order weak Lagrangian from the corresponding strong one. This
model is found to be equivalent to the previous one for 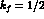 [26]. Clearly, from the outset the above models for the weak
constants do not refer to resonances. The latter are introduced once the
strong couplings are saturated by resonance exchange.
[26]. Clearly, from the outset the above models for the weak
constants do not refer to resonances. The latter are introduced once the
strong couplings are saturated by resonance exchange.
Vector-meson dominance was initially considered in Ref. [42],
limiting to the  component of the weak Hamiltonian. Due to Bose
statistics, by their vectorial nature spin-one
mesons can only contribute to the amplitudes
component of the weak Hamiltonian. Due to Bose
statistics, by their vectorial nature spin-one
mesons can only contribute to the amplitudes 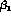 and
and 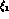 , because
they couple only to final states antisymmetric under exchange of two pions,
so that only the constant
, because
they couple only to final states antisymmetric under exchange of two pions,
so that only the constant 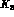 in (30) would be nonzero,
while
in (30) would be nonzero,
while 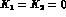 . In addition, in the factorization model with only
vector-meson exchange, also
. In addition, in the factorization model with only
vector-meson exchange, also  is found to vanish [42].
Therefore, having been determined phenomenologically to be
non-zero within uncertainties {[5], weak counterterms are
likely not to be dominated by vector-meson exchange. This might signal
a situation rather different from the strong interaction case.
is found to vanish [42].
Therefore, having been determined phenomenologically to be
non-zero within uncertainties {[5], weak counterterms are
likely not to be dominated by vector-meson exchange. This might signal
a situation rather different from the strong interaction case.
Even limiting to the  component, the general structure of
component, the general structure of
 including both spin-zero and spin-one resonance exchanges
introduces too many weak resonance couplings,
and no simplification of the
including both spin-zero and spin-one resonance exchanges
introduces too many weak resonance couplings,
and no simplification of the 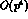 chiral structure of
chiral structure of  would be obtained at the general stage, without assuming a
model [26].
would be obtained at the general stage, without assuming a
model [26].
In the factorization model, where vectors do not contribute, finite values of
the constants 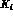 can result only from spin-zero meson exchange, which
would imply
can result only from spin-zero meson exchange, which
would imply  and
and  in Eq. (30). The
phenomenologically determined constants do not seem to agree with these
predictions. Furthermore, the size of
in Eq. (30). The
phenomenologically determined constants do not seem to agree with these
predictions. Furthermore, the size of 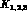 , predicted by using
the scalar resonance couplings determined in Ref. [39], does not
compare well with the phenomenological determinations, unless the value of
, predicted by using
the scalar resonance couplings determined in Ref. [39], does not
compare well with the phenomenological determinations, unless the value of
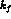 is chosen very far from unity. Interpreted pessimistically, this might
indicate a trouble for the factorization model. However, such a comparison
might not be completely conclusive yet, considering the
uncertainties which affect the present determinations of the constants
is chosen very far from unity. Interpreted pessimistically, this might
indicate a trouble for the factorization model. However, such a comparison
might not be completely conclusive yet, considering the
uncertainties which affect the present determinations of the constants
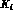 . These uncertainties are induced by the experimental ones, and also
in large part by the inaccuracies of the strong couplings determinations
that are used as input in the `chiral fit'. In addition, the strong
scale-dependence of the
. These uncertainties are induced by the experimental ones, and also
in large part by the inaccuracies of the strong couplings determinations
that are used as input in the `chiral fit'. In addition, the strong
scale-dependence of the  complicates the comparison with models at
the present stage.
complicates the comparison with models at
the present stage.



Next: 6 Measurements at the
Up: 5.2 Factorization and resonance
Previous: 5.2.1 Large calculations
Carlos E.Piedrafita
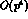 strong
interaction constants. Also, it improves the theoretical description,
by giving a well-recognizable physical meaning to the counterterms. By
construction, this determination of counterterms is
strong
interaction constants. Also, it improves the theoretical description,
by giving a well-recognizable physical meaning to the counterterms. By
construction, this determination of counterterms is  -independent, so
that, in principle, the comparison with the scale-dependent matrix elements of
-independent, so
that, in principle, the comparison with the scale-dependent matrix elements of
 has some ambiguity. Nevertheless, it was shown that
meson exchanges almost entirely saturate those couplings, as being in
good agreement with the values determined phenomenologically from
experimental data in Ref. [21], if the scale
has some ambiguity. Nevertheless, it was shown that
meson exchanges almost entirely saturate those couplings, as being in
good agreement with the values determined phenomenologically from
experimental data in Ref. [21], if the scale 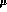 is chosen between,
say,
is chosen between,
say,  and
and 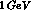 [39,40]. This suggests
that a similar meson-exchange dominance could work also for the weak
constants needed in
[39,40]. This suggests
that a similar meson-exchange dominance could work also for the weak
constants needed in 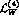 . However, while there exists enough
information to experimentally determine the strong resonance couplings
needed for the
. However, while there exists enough
information to experimentally determine the strong resonance couplings
needed for the 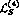 counterterms, in the case of
counterterms, in the case of
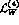 the situation is complicated by the additional need of
weak resonance couplings to pseudoscalar mesons, which are not known
and can only be calculated within specific models. Clearly, as a common
feature, the role of such models is to relate the weak
the situation is complicated by the additional need of
weak resonance couplings to pseudoscalar mesons, which are not known
and can only be calculated within specific models. Clearly, as a common
feature, the role of such models is to relate the weak  constants to
the strong constants, the only ones which are known.
constants to
the strong constants, the only ones which are known.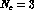 ).
In this case, the strong counterterms needed in the
next-to-leading terms are phenomenologically determined either directly from
experiment or via the resonance exchange parametrization. More
precisely, in the application of Ref. [
).
In this case, the strong counterterms needed in the
next-to-leading terms are phenomenologically determined either directly from
experiment or via the resonance exchange parametrization. More
precisely, in the application of Ref. [ a free coefficient
a free coefficient
 is introduced in the factorized expression of
is introduced in the factorized expression of 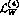 , so
that naive factorization would correspond to
, so
that naive factorization would correspond to  . Another proposed model
is the so-called `weak deformation model' [
. Another proposed model
is the so-called `weak deformation model' [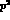 , the weak nonleptonic
Lagrangian can be directly obtained from the strong one by
means of a suitable transformation, called `deformation', and (ii) the
requirement that the same `deformation' generates, more in general, also the
higher order weak Lagrangian from the corresponding strong one. This
model is found to be equivalent to the previous one for
, the weak nonleptonic
Lagrangian can be directly obtained from the strong one by
means of a suitable transformation, called `deformation', and (ii) the
requirement that the same `deformation' generates, more in general, also the
higher order weak Lagrangian from the corresponding strong one. This
model is found to be equivalent to the previous one for 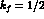 [
[ component of the weak Hamiltonian. Due to Bose
statistics, by their vectorial nature spin-one
mesons can only contribute to the amplitudes
component of the weak Hamiltonian. Due to Bose
statistics, by their vectorial nature spin-one
mesons can only contribute to the amplitudes 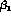 and
and 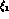 , because
they couple only to final states antisymmetric under exchange of two pions,
so that only the constant
, because
they couple only to final states antisymmetric under exchange of two pions,
so that only the constant 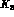 in (
in (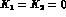 . In addition, in the factorization model with only
vector-meson exchange, also
. In addition, in the factorization model with only
vector-meson exchange, also  is found to vanish [
is found to vanish [ component, the general structure of
component, the general structure of
 including both spin-zero and spin-one resonance exchanges
introduces too many weak resonance couplings,
and no simplification of the
including both spin-zero and spin-one resonance exchanges
introduces too many weak resonance couplings,
and no simplification of the 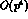 chiral structure of
chiral structure of  would be obtained at the general stage, without assuming a
model [
would be obtained at the general stage, without assuming a
model [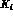 can result only from spin-zero meson exchange, which
would imply
can result only from spin-zero meson exchange, which
would imply  and
and  in Eq. (
in Eq. (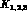 , predicted by using
the scalar resonance couplings determined in Ref. [
, predicted by using
the scalar resonance couplings determined in Ref. [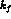 is chosen very far from unity. Interpreted pessimistically, this might
indicate a trouble for the factorization model. However, such a comparison
might not be completely conclusive yet, considering the
uncertainties which affect the present determinations of the constants
is chosen very far from unity. Interpreted pessimistically, this might
indicate a trouble for the factorization model. However, such a comparison
might not be completely conclusive yet, considering the
uncertainties which affect the present determinations of the constants
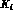 . These uncertainties are induced by the experimental ones, and also
in large part by the inaccuracies of the strong couplings determinations
that are used as input in the `chiral fit'. In addition, the strong
scale-dependence of the
. These uncertainties are induced by the experimental ones, and also
in large part by the inaccuracies of the strong couplings determinations
that are used as input in the `chiral fit'. In addition, the strong
scale-dependence of the  complicates the comparison with models at
the present stage.
complicates the comparison with models at
the present stage.