
For convenience, we recall the Standard Model non-leptonic weak effective Lagrangian in terms of quark fields [16]:
where 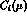 are numerical coefficients depending on heavy masses and
calculable in perturbative QCD, and
are numerical coefficients depending on heavy masses and
calculable in perturbative QCD, and  are local four-quark operators
with
are local four-quark operators
with 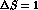 and
and 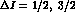 [17]. Both
[17]. Both 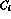 and
and  depend on a renormalization scale
depend on a renormalization scale 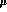 , but their product must be
, but their product must be
 -independent to ensure independence of physical amplitudes from this
scale.
-independent to ensure independence of physical amplitudes from this
scale.
To make theoretical predictions, and thus compare the quark-level
transition Lagrangian (18) with experimental data, one must estimate
matrix elements of the four-quark operators between initial  and final
and final 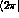 and
and 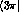 hadronic states. These
matrix elements crucially depend on the nonperturbative structure of
low-energy QCD, so that calculations relying on different hadronization
schemes should be model dependent. The chiral Lagrangian technique provides
a general framework for such matrix elements, and is essentially based on
the transformation properties of the operators in Eq. (18) under
separate
hadronic states. These
matrix elements crucially depend on the nonperturbative structure of
low-energy QCD, so that calculations relying on different hadronization
schemes should be model dependent. The chiral Lagrangian technique provides
a general framework for such matrix elements, and is essentially based on
the transformation properties of the operators in Eq. (18) under
separate  rotations of left-handed and
of right-handed fields, i.e. the chiral
rotations of left-handed and
of right-handed fields, i.e. the chiral 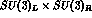 symmetry
transformations (
symmetry
transformations (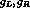 ).
).
At the scale  , the basis of operators can be chosen as
(
, the basis of operators can be chosen as
( ):
):
where color indices are implicitly contracted within each quark-bilinear
factor. The `V-A' operators  and
and 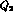 have selection rule
have selection rule
 and behave as
and behave as  ; the
penguin operators
; the
penguin operators  ,
,  and
and 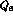 are purely
are purely  , and
transform as
, and
transform as  ; the electroweak penguin operators
; the electroweak penguin operators  and
and 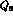 transform as
transform as  , and have both
, and have both 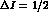 and
and  components. Electropenguin operators are suppressed by a small
coefficient of order
components. Electropenguin operators are suppressed by a small
coefficient of order 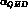 , so they must be considered only in the
CP violating case [11].
, so they must be considered only in the
CP violating case [11].
Accordingly, limiting to the operators  , the
lowest order,
, the
lowest order,  , weak chiral Lagrangian is the sum of a (
, weak chiral Lagrangian is the sum of a (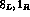 )
operator plus a (
)
operator plus a (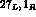 ) one, whose forms are uniquely dictated by
chiral symmetry [18]:
) one, whose forms are uniquely dictated by
chiral symmetry [18]:
Here,  with
with
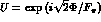 , and
, and  is the pseudoscalar meson
is the pseudoscalar meson
 matrix, so that U transforms under
matrix, so that U transforms under 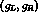 as
as
 [19]:
[19]:
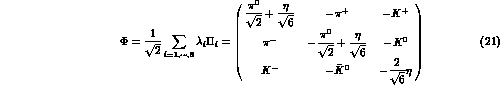
The matrices  and the coefficients
and the coefficients 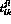 that appear in
(20) can be found, e.g., in
[20,5]. The octet and 27-plet coupling constants
that appear in
(20) can be found, e.g., in
[20,5]. The octet and 27-plet coupling constants  and
and  , the only two parameters needed at order
, the only two parameters needed at order  in
in  ,
cannot be estimated theoretically, but must be phenomenologically fitted from
experimental data.
,
cannot be estimated theoretically, but must be phenomenologically fitted from
experimental data.
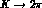 and
and  amplitudes at order
amplitudes at order  are obtained from the `tree' diagrams in Fig. 2, where the needed
weak vertices are obtained by expanding
the effective Lagrangian (20)
to the right number of pseudoscalar meson fields. As shown in Fig. 2, in the
case of
are obtained from the `tree' diagrams in Fig. 2, where the needed
weak vertices are obtained by expanding
the effective Lagrangian (20)
to the right number of pseudoscalar meson fields. As shown in Fig. 2, in the
case of  also `pole diagrams' appear, which involve the
four-meson strong interaction. At the order
also `pole diagrams' appear, which involve the
four-meson strong interaction. At the order  , this is represented
by the chiral Lagrangian [21,19]
, this is represented
by the chiral Lagrangian [21,19]
where 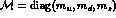 is the quark mass matrix, explicitly
breaking chiral symmetry, and B is a constant such that, to leading order,
is the quark mass matrix, explicitly
breaking chiral symmetry, and B is a constant such that, to leading order,
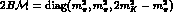 in the
in the  limit.
limit.

Figure 2: Lowest order diagrams ( ) for
) for  and
and
 : the weak vertex is represented by
: the weak vertex is represented by
 , the strong one by
, the strong one by  .
.
Defining 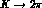 amplitudes as
amplitudes as  and
and
 , with the usual isospin decomposition
, with the usual isospin decomposition
the diagrams in Fig. 2 directly give for the 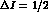 amplitudes:
amplitudes:
and for the 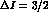 amplitudes:
amplitudes:
Although, in principle, at this level 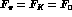 ,
, 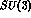 breaking is
phenomenologically included by using
breaking is
phenomenologically included by using  .
.
As anticipated, Eqs. (24) and (25) manifestly
express the current algebra soft-pion theorems relating 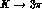 amplitudes with vanishing pion four-momentum to
amplitudes with vanishing pion four-momentum to  ones, and also
include finite pion mass corrections extrapolating those relations back
into the physical region.
ones, and also
include finite pion mass corrections extrapolating those relations back
into the physical region.
Indeed, the values of the coupling constants 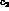 and
and 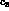 can be obtained
by fitting (24) and (25) to the experimental
can be obtained
by fitting (24) and (25) to the experimental
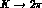 amplitudes. The results, displaying the
amplitudes. The results, displaying the  enhancement in
enhancement in  , are shown in the third column of
Tab. 5.
, are shown in the third column of
Tab. 5.

Table 5: Isospin amplitudes and relative phase for 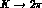 .
.
The so determined constants  and
and  can be used in
Eqs. (24) and (25) to predict the
can be used in
Eqs. (24) and (25) to predict the
 isospin amplitudes at
isospin amplitudes at  .
.![]() These predictions are
reported in the second column of Tab. 6. Comparing with the numbers in
Tab. 4, one can see that the order
These predictions are
reported in the second column of Tab. 6. Comparing with the numbers in
Tab. 4, one can see that the order  is in reasonable agreement with the
data, as it underestimates the experimental amplitudes, on the average, by
about 20-35%. This is not surprising, as the expected size of next-to-leading corrections,
of order
is in reasonable agreement with the
data, as it underestimates the experimental amplitudes, on the average, by
about 20-35%. This is not surprising, as the expected size of next-to-leading corrections,
of order  , is
, is  , where
, where
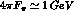 is the scale of chiral symmetry
breaking. We should also remark, from Tab. 4, that the amplitude
is the scale of chiral symmetry
breaking. We should also remark, from Tab. 4, that the amplitude
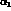 is so well measured that it really represents a challenge to the
theory. On the other hand, the discrepancy of the theoretical prediction
with the central value of the
is so well measured that it really represents a challenge to the
theory. On the other hand, the discrepancy of the theoretical prediction
with the central value of the 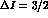 slope
slope  seems rather sizable. Consequently, it would be desirable to significantly
improve the experimental accuracy on this parameter. We remark, also,
that both the final state strong interaction phases and the quadratic slopes
vanish at this order in
seems rather sizable. Consequently, it would be desirable to significantly
improve the experimental accuracy on this parameter. We remark, also,
that both the final state strong interaction phases and the quadratic slopes
vanish at this order in  , reflecting, respectively, the `tree'
diagram approximation of Fig. 2 where there are no absorptive parts, and
the use of the two-derivative Lagrangian (20) which cannot
provide enough powers in momenta.
, reflecting, respectively, the `tree'
diagram approximation of Fig. 2 where there are no absorptive parts, and
the use of the two-derivative Lagrangian (20) which cannot
provide enough powers in momenta.
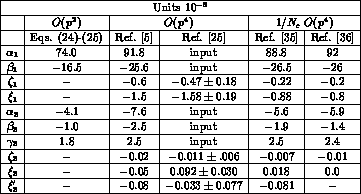
Table 6: Theoretical predictions for  isospin amplitudes.
isospin amplitudes.
The deviations of the  predictions from the experimental values of
constant and linear amplitudes, and the evidence for non-vanishing quadratic
slopes, call for the introduction of the next-to-leading chiral
corrections. The general form of the
predictions from the experimental values of
constant and linear amplitudes, and the evidence for non-vanishing quadratic
slopes, call for the introduction of the next-to-leading chiral
corrections. The general form of the  non-leptonic Lagrangian at
order
non-leptonic Lagrangian at
order  ,
, 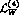 , was worked out in Ref. [20].
The number of new independent local operators, allowed by the symmetry to
contribute to
, was worked out in Ref. [20].
The number of new independent local operators, allowed by the symmetry to
contribute to 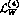 , whose coupling constants are not
determined theoretically, is in general unmanageably large. In this set,
there are four-derivative operators, which contribute
, whose coupling constants are not
determined theoretically, is in general unmanageably large. In this set,
there are four-derivative operators, which contribute 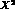 and
and 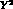 terms
to
terms
to 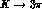 matrix elements and thus determine the quadratic slopes in
Eqs. (14) or (15), such as the
matrix elements and thus determine the quadratic slopes in
Eqs. (14) or (15), such as the  operators of the form [23]:
operators of the form [23]:
and others. There are, also, a multitude of operators with higher derivatives of meson fields, etc..
Four-derivative operators obviously vanish at soft-pion points and thus
cannot contribute to  , so that
no information on them can be derived from the
, so that
no information on them can be derived from the  sector, as it is
the case of
sector, as it is
the case of  and
and 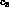 at the leading order
at the leading order  . On the other
hand, apart from (small) corrections of order
. On the other
hand, apart from (small) corrections of order  , higher
order operators contributing to both
, higher
order operators contributing to both 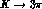 and
and  , but not
contributing
, but not
contributing 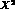 and
and  terms, preserve the leading order
relations between
terms, preserve the leading order
relations between  and
and 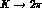 . Consequently, they can be
absorbed in the definition of the physical
. Consequently, they can be
absorbed in the definition of the physical  amplitudes or,
equivalently, in a redefinition of the coupling constants
amplitudes or,
equivalently, in a redefinition of the coupling constants  and
and  .
.
It turns out that for 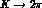 and
and 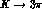 decays the situation
considerably simplifies, because only seven linear combinations of the
possible
decays the situation
considerably simplifies, because only seven linear combinations of the
possible 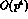 local operators in
local operators in 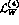 are found to be
active in these processes [5]. The discussion of the analogous,
order
are found to be
active in these processes [5]. The discussion of the analogous,
order 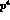 , weak Lagrangian for non-leptonic radiative kaon decays, and a
presentation of the relevant phenomenology, can be found in
Ref. [24].
, weak Lagrangian for non-leptonic radiative kaon decays, and a
presentation of the relevant phenomenology, can be found in
Ref. [24].
Specifically, denoting by  any of the
any of the 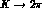 and
and  amplitudes up to order
amplitudes up to order  , we have
, we have
where  is the leading order, and
is the leading order, and 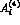 is the next-to-leading
correction. As pictorially
is the next-to-leading
correction. As pictorially

Figure 3: Examples of 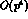 contributions to
contributions to 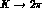 and
and
 :
:  and
and  have the same meaning as
in Fig. 2.
have the same meaning as
in Fig. 2.
represented in Fig. 3, the latter can be decomposed as:
In Eq. (28),  represents the contribution
from chiral loop diagrams,
represents the contribution
from chiral loop diagrams,![]() and
and 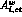 accounts for the tree diagram
accounts for the tree diagram 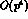 weak counterterm contributions in
Fig. 3, connected to the above mentioned higher dimension operators
determining
weak counterterm contributions in
Fig. 3, connected to the above mentioned higher dimension operators
determining  , with a priori unknown
low-energy coupling constants to be determined phenomenologically from data
on
, with a priori unknown
low-energy coupling constants to be determined phenomenologically from data
on  and
and  . In addition, there appear a number of
. In addition, there appear a number of
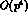 strong interaction counterterms, which determine
strong interaction counterterms, which determine  needed in the pole diagrams of Fig. 3, but these constants are already
available from the analyses of the strong interaction sector
[21,19], and therefore do not introduce anything unknown.
needed in the pole diagrams of Fig. 3, but these constants are already
available from the analyses of the strong interaction sector
[21,19], and therefore do not introduce anything unknown.
Counterterms regulate loop divergences, and in general both contributions
separately depend (logarithmically) on a renormalization scale  , such
that their sum in (28) is scale-independent.
, such
that their sum in (28) is scale-independent.
As for the structure of the seven weak counterterm contributions to the
individual amplitudes, denoting their coupling constants by
 , neglecting
the tiny
, neglecting
the tiny  component of
component of  and (small) corrections of order
and (small) corrections of order
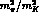 , and adding the lowest order Eqs. (24) and
(25), one finds for the
, and adding the lowest order Eqs. (24) and
(25), one finds for the 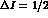
 amplitude the complete expression [5,25]:
amplitude the complete expression [5,25]:
and, absorbing the counterterm coupling 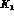 in
in  , for the
, for the 
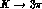 amplitudes:
amplitudes:
Likewise, in the 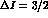 sector:
sector:
and, absorbing the counterterm  in the definition of
in the definition of
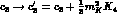 :
:
where 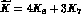 . Eqs. (30)-(32)
imply the following consistency conditions among the
. Eqs. (30)-(32)
imply the following consistency conditions among the  weak counterterm
contributions:
weak counterterm
contributions:
The strategy followed by the authors of Ref. [5], to
phenomenologically determine the weak coupling constants
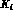 , is to fit to the experimental data in Tabs. 4 and 5 the full
theoretical structure of
, is to fit to the experimental data in Tabs. 4 and 5 the full
theoretical structure of 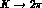 and
and 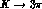 isospin
amplitudes up to order
isospin
amplitudes up to order  , with the calculated one-loop diagrams and the
determinations of strong counterterms of Ref. [21] as inputs.
, with the calculated one-loop diagrams and the
determinations of strong counterterms of Ref. [21] as inputs.
The resulting numerical values of the weak counterterm constants, and of
the calculated one-loop contributions, are presented in Ref. [5]
for the renormalization scale 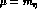 , which minimizes loop diagrams
with intermediate kaons and etas. It is interesting that the
, which minimizes loop diagrams
with intermediate kaons and etas. It is interesting that the  pattern, dominant at order
pattern, dominant at order 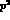 , turns out to be reproduced also at the
order
, turns out to be reproduced also at the
order  level by weak counterterms. The values of loops and counterterms
at other renormalization scales, such as
level by weak counterterms. The values of loops and counterterms
at other renormalization scales, such as 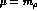 and
and
 , can be found in Ref. [26], and show that the
separate scale dependences of these contributions can be quite sizable.
, can be found in Ref. [26], and show that the
separate scale dependences of these contributions can be quite sizable.
In Tabs. 5 and 6 we report the numerical results of the above mentioned
`chiral fit' for the 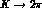 and
and 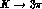 amplitudes, respectively.
>From Tab. 5 it is important to notice that the renormalization of the octet
and 27-plet coupling constants
amplitudes, respectively.
>From Tab. 5 it is important to notice that the renormalization of the octet
and 27-plet coupling constants  and
and  from the order
from the order  values,
due to the
values,
due to the 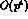 corrections, is substantial
(about 30%) in the case of the former, while the latter remains practically
unaffected. As for the
corrections, is substantial
(about 30%) in the case of the former, while the latter remains practically
unaffected. As for the 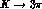 amplitudes, the comparison of
the numbers in the third column of Tab. 6 with those in Tab. 4 shows
that the theoretical structure including the next-to-leading chiral
corrections is able to well-reproduce the constant and linear amplitudes for
all channels, in particular to accomodate the phenomenological observation
that such corrections should be somewhat larger in the
amplitudes, the comparison of
the numbers in the third column of Tab. 6 with those in Tab. 4 shows
that the theoretical structure including the next-to-leading chiral
corrections is able to well-reproduce the constant and linear amplitudes for
all channels, in particular to accomodate the phenomenological observation
that such corrections should be somewhat larger in the
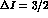 sector. Clearly, this is very encouraging and supports the
chiral Lagrangian picture. On the other hand, due to the large
experimental uncertainties, the situation for the quadratic
slopes is not as well-defined, specially for the
sector. Clearly, this is very encouraging and supports the
chiral Lagrangian picture. On the other hand, due to the large
experimental uncertainties, the situation for the quadratic
slopes is not as well-defined, specially for the  ones which
are expected to be suppressed, so that a real clarification should wait for
better data.
ones which
are expected to be suppressed, so that a real clarification should wait for
better data.
In fact, in this regard, one could try to go beyond the global fitting
procedure, and take advantage of the consistency relations
(33) and (34) among weak counterterm
contributions [25]. Once  and
and 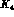 are absorbed in the
are absorbed in the
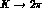 amplitudes giving the new values of
amplitudes giving the new values of 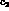 and
and 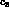 , and the
remaining five weak counterterms are fitted from the (best determined)
constant and linear
, and the
remaining five weak counterterms are fitted from the (best determined)
constant and linear 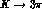 amplitudes, the quadratic amplitudes can be
parameter-free predicted. Actually, these would represent the true, genuine
predictions of
amplitudes, the quadratic amplitudes can be
parameter-free predicted. Actually, these would represent the true, genuine
predictions of 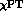 at
at 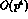 , and accordingly provide the
non-trivial test of this framework.
, and accordingly provide the
non-trivial test of this framework.
Such predictions for the quadratic amplitudes are reported in the
fourth column of Tab. 6. The comparison with the determinations in Tab. 4 is
remarkably successful for the 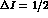 amplitudes. It is not as good
for the
amplitudes. It is not as good
for the  slopes. However, these are given by the
difference of two (almost cancelling) large numbers, so that uncertainties
can have a dramatic effect in this case. To give an idea, we notice that,
for
slopes. However, these are given by the
difference of two (almost cancelling) large numbers, so that uncertainties
can have a dramatic effect in this case. To give an idea, we notice that,
for  , the value of the Dalitz plot parameter h predicted
by Tab. 6 combined with the expansion (15) would be
, the value of the Dalitz plot parameter h predicted
by Tab. 6 combined with the expansion (15) would be
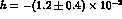 . Direct use of the determinations in Tab. 4
would give, instead,
. Direct use of the determinations in Tab. 4
would give, instead,  ,
to finally compare with the recent experimental measurement reported in Tab. 2,
,
to finally compare with the recent experimental measurement reported in Tab. 2,
 [14].
Indeed, by combining their result with the experimental determinations of h
for the charged kaon decay modes, the authors of [14]
would find the rather large ratio of
[14].
Indeed, by combining their result with the experimental determinations of h
for the charged kaon decay modes, the authors of [14]
would find the rather large ratio of  to
to 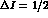 amplitudes
amplitudes 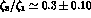 .
All this shows, on the one side, the crucial role of quadratic
amplitudes, in particular of the
.
All this shows, on the one side, the crucial role of quadratic
amplitudes, in particular of the 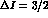 ones, as tests of
the
ones, as tests of
the  framework, and, on the other side, that possible
discrepancies should not be considered as conclusive at the present level of
accuracy.
framework, and, on the other side, that possible
discrepancies should not be considered as conclusive at the present level of
accuracy.
Therefore, further experimental work attempting to improve the
determinations of 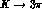 isospin amplitudes, in particular of the
isospin amplitudes, in particular of the
 and the
and the 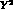 terms, is required for more significant tests. In this
regard, to substantially reduce theoretical uncertainties, more accurate
determinations of the strong counterterms, dominating the pole diagram
contributions in Fig. 3, should be extremely useful and would lead to
more precise determinations of the weak counterterms. Also, the order
terms, is required for more significant tests. In this
regard, to substantially reduce theoretical uncertainties, more accurate
determinations of the strong counterterms, dominating the pole diagram
contributions in Fig. 3, should be extremely useful and would lead to
more precise determinations of the weak counterterms. Also, the order
 is the leading one for quadratic amplitudes so that, in principle,
their predicted values at this level stand on a less firm footing
with respect to constant and linear terms. Therefore, uncertainties
of the order of 20-40% from
is the leading one for quadratic amplitudes so that, in principle,
their predicted values at this level stand on a less firm footing
with respect to constant and linear terms. Therefore, uncertainties
of the order of 20-40% from  corrections, affecting the predictions
for quadratic terms in Tab. 6, should be kept in mind
until some quantitative assessment of such higher order effects is available.
Finally, in the quest of most reliable predictions, considering
that substantial QED effects can possibly affect quadratic
amplitudes [27,28], further theoretical work should also be
directed to improved estimates of isospin breaking corrections.
corrections, affecting the predictions
for quadratic terms in Tab. 6, should be kept in mind
until some quantitative assessment of such higher order effects is available.
Finally, in the quest of most reliable predictions, considering
that substantial QED effects can possibly affect quadratic
amplitudes [27,28], further theoretical work should also be
directed to improved estimates of isospin breaking corrections.
The order  loop diagrams in Fig. 3, with on-shell propagators in internal
lines, generate the final state interaction imaginary parts at the
leading order. For
loop diagrams in Fig. 3, with on-shell propagators in internal
lines, generate the final state interaction imaginary parts at the
leading order. For  this mechanism generates the strong interaction
relative phase
this mechanism generates the strong interaction
relative phase  between the two isospin amplitudes. The
determination of this phase obtained by the fit of Ref. [5],
reported in Tab. 5, is in reasonable agreement with the value directly
measured in
between the two isospin amplitudes. The
determination of this phase obtained by the fit of Ref. [5],
reported in Tab. 5, is in reasonable agreement with the value directly
measured in  -
- scattering,
scattering,
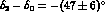 [29], the small discrepancy
being due to the neglect of isospin breaking and electromagnetic
corrections in
[29], the small discrepancy
being due to the neglect of isospin breaking and electromagnetic
corrections in  amplitudes. From the fourth column of Tab. 5 we see that the leading
order somewhat underestimates
amplitudes. From the fourth column of Tab. 5 we see that the leading
order somewhat underestimates  . This is not surprising,
since in this channel the relevant
. This is not surprising,
since in this channel the relevant  -
- phase shifts are evaluated at
phase shifts are evaluated at
 , a rather high energy from the point of view of
, a rather high energy from the point of view of
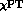 , so that ones expects a large contribution from the
next order in momenta [30].
, so that ones expects a large contribution from the
next order in momenta [30].
As emphasized in the previous section, due to the small Q-values, final
state interaction phases in  are much more directly relevant to
the low-energy regime, where leading order calculations should be most
reliable. Explicit expressions of rescattering at leading order in
are much more directly relevant to
the low-energy regime, where leading order calculations should be most
reliable. Explicit expressions of rescattering at leading order in
 can be found in [31,22] and, in the
framework of the rescattering matrix, in [12]. Numerical
results for both real and imaginary parts of the loop amplitudes are also
given in Ref. [5]. However, the explicit kinematical dependence is
needed in addition, in order to unambiguously reconstruct the rescattering
matrix. In particular, for the coefficients of the expansion around the
centre of the Dalitz plot in Eq. (14), we find:
can be found in [31,22] and, in the
framework of the rescattering matrix, in [12]. Numerical
results for both real and imaginary parts of the loop amplitudes are also
given in Ref. [5]. However, the explicit kinematical dependence is
needed in addition, in order to unambiguously reconstruct the rescattering
matrix. In particular, for the coefficients of the expansion around the
centre of the Dalitz plot in Eq. (14), we find:
An experimental verification of these predictions would also be of relevance
to the chiral test.![]()