


Next: 5.1 Chiral perturbation theory
Up: Chapter 6 Section 1
Previous: 4 Experimental determinations
Due to the low kinetic energy available to final state pions,
 seems the ideal process where to apply the notion of the
Goldstone-boson nature of pseudoscalar mesons, and the related low-energy
expansions of transition amplitudes, that are obtained from the chiral
Lagrangian realization of the nonleptonic
seems the ideal process where to apply the notion of the
Goldstone-boson nature of pseudoscalar mesons, and the related low-energy
expansions of transition amplitudes, that are obtained from the chiral
Lagrangian realization of the nonleptonic  weak interaction.
Such a Lagrangian, written in terms of
Goldstone boson-pseudoscalar meson fields
weak interaction.
Such a Lagrangian, written in terms of
Goldstone boson-pseudoscalar meson fields 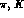 and
and 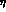 , has
the same transformation properties under unitary symmetry as the four-quark
Lagrangian originally derived in the framework of the short distance operator
product expansion, and automatically
accounts for general properties of non-perturbative strong interactions
governed by long-distance QCD. By the feature of the Goldstone boson
interaction, of vanishing in the zero four-momentum limit, this formalism
leads to amplitudes expansions in powers of pseudoscalar meson masses and
energies which, in particular, naturally incorporate the current algebra
soft-pion theorems. These theorems are rigorously valid in the chiral
symmetry limit and, in the specific case of kaon nonleptonic decays,
relate
, has
the same transformation properties under unitary symmetry as the four-quark
Lagrangian originally derived in the framework of the short distance operator
product expansion, and automatically
accounts for general properties of non-perturbative strong interactions
governed by long-distance QCD. By the feature of the Goldstone boson
interaction, of vanishing in the zero four-momentum limit, this formalism
leads to amplitudes expansions in powers of pseudoscalar meson masses and
energies which, in particular, naturally incorporate the current algebra
soft-pion theorems. These theorems are rigorously valid in the chiral
symmetry limit and, in the specific case of kaon nonleptonic decays,
relate  to
to  amplitudes making use solely of
the chiral
amplitudes making use solely of
the chiral  transformation properties (as a
right-handed singlet) of the nonleptonic weak hamiltonian [15].
They can be written symbolically, with
transformation properties (as a
right-handed singlet) of the nonleptonic weak hamiltonian [15].
They can be written symbolically, with  the
pion decay constant, as:
the
pion decay constant, as:

where 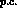 and
and  mean parity-conserving and parity-violating
components, and similar relations hold for the other pions becoming
soft and for the different decay channels. Actually, soft-pion points
are somewhat far from the kinematically allowed region of the Dalitz plot,
where mesons have small, but finite, four-momenta. Thus, in addition to
providing a general, and convenient, computational tool to evaluate the
relevant hadronic matrix elements of
mean parity-conserving and parity-violating
components, and similar relations hold for the other pions becoming
soft and for the different decay channels. Actually, soft-pion points
are somewhat far from the kinematically allowed region of the Dalitz plot,
where mesons have small, but finite, four-momenta. Thus, in addition to
providing a general, and convenient, computational tool to evaluate the
relevant hadronic matrix elements of 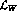 directly in terms of Feynman
diagrams with pion, kaon and eta fields, one advantage of the effective
chiral Lagrangian approach is that it gives a consistent, unambiguous
prescription to extrapolate soft-pion theorem predictions into the physical
region.
directly in terms of Feynman
diagrams with pion, kaon and eta fields, one advantage of the effective
chiral Lagrangian approach is that it gives a consistent, unambiguous
prescription to extrapolate soft-pion theorem predictions into the physical
region.
Actually, such a Lagrangian depends on a number of
phenomenological coupling constants (increasing with the desired
order in the momentum expansion), whose values cannot be predicted
theoretically from the symmetry but, instead, must be inferred from
experiment. To account for both the leading 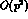 and the
next-to-leading
and the
next-to-leading 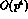 corrections in the
corrections in the 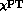 expansion,
a considerable number of such constants are needed. Fortunately, this number is
limited enough for the scheme to remain predictive, and to be
severely tested by accurate experimental data on
expansion,
a considerable number of such constants are needed. Fortunately, this number is
limited enough for the scheme to remain predictive, and to be
severely tested by accurate experimental data on
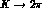 and
and  . In the next section, we briefly review the
application of
. In the next section, we briefly review the
application of  to
to 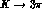 .
.



Next: 5.1 Chiral perturbation theory
Up: Chapter 6 Section 1
Previous: 4 Experimental determinations
Carlos E.Piedrafita
 seems the ideal process where to apply the notion of the
Goldstone-boson nature of pseudoscalar mesons, and the related low-energy
expansions of transition amplitudes, that are obtained from the chiral
Lagrangian realization of the nonleptonic
seems the ideal process where to apply the notion of the
Goldstone-boson nature of pseudoscalar mesons, and the related low-energy
expansions of transition amplitudes, that are obtained from the chiral
Lagrangian realization of the nonleptonic  weak interaction.
Such a Lagrangian, written in terms of
Goldstone boson-pseudoscalar meson fields
weak interaction.
Such a Lagrangian, written in terms of
Goldstone boson-pseudoscalar meson fields 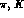 and
and 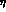 , has
the same transformation properties under unitary symmetry as the four-quark
Lagrangian originally derived in the framework of the short distance operator
product expansion, and automatically
accounts for general properties of non-perturbative strong interactions
governed by long-distance QCD. By the feature of the Goldstone boson
interaction, of vanishing in the zero four-momentum limit, this formalism
leads to amplitudes expansions in powers of pseudoscalar meson masses and
energies which, in particular, naturally incorporate the current algebra
soft-pion theorems. These theorems are rigorously valid in the chiral
symmetry limit and, in the specific case of kaon nonleptonic decays,
relate
, has
the same transformation properties under unitary symmetry as the four-quark
Lagrangian originally derived in the framework of the short distance operator
product expansion, and automatically
accounts for general properties of non-perturbative strong interactions
governed by long-distance QCD. By the feature of the Goldstone boson
interaction, of vanishing in the zero four-momentum limit, this formalism
leads to amplitudes expansions in powers of pseudoscalar meson masses and
energies which, in particular, naturally incorporate the current algebra
soft-pion theorems. These theorems are rigorously valid in the chiral
symmetry limit and, in the specific case of kaon nonleptonic decays,
relate  to
to  amplitudes making use solely of
the chiral
amplitudes making use solely of
the chiral  transformation properties (as a
right-handed singlet) of the nonleptonic weak hamiltonian [15].
They can be written symbolically, with
transformation properties (as a
right-handed singlet) of the nonleptonic weak hamiltonian [15].
They can be written symbolically, with  the
pion decay constant, as:
the
pion decay constant, as:

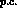 and
and  mean parity-conserving and parity-violating
components, and similar relations hold for the other pions becoming
soft and for the different decay channels. Actually, soft-pion points
are somewhat far from the kinematically allowed region of the Dalitz plot,
where mesons have small, but finite, four-momenta. Thus, in addition to
providing a general, and convenient, computational tool to evaluate the
relevant hadronic matrix elements of
mean parity-conserving and parity-violating
components, and similar relations hold for the other pions becoming
soft and for the different decay channels. Actually, soft-pion points
are somewhat far from the kinematically allowed region of the Dalitz plot,
where mesons have small, but finite, four-momenta. Thus, in addition to
providing a general, and convenient, computational tool to evaluate the
relevant hadronic matrix elements of 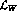 directly in terms of Feynman
diagrams with pion, kaon and eta fields, one advantage of the effective
chiral Lagrangian approach is that it gives a consistent, unambiguous
prescription to extrapolate soft-pion theorem predictions into the physical
region.
directly in terms of Feynman
diagrams with pion, kaon and eta fields, one advantage of the effective
chiral Lagrangian approach is that it gives a consistent, unambiguous
prescription to extrapolate soft-pion theorem predictions into the physical
region.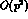 and the
next-to-leading
and the
next-to-leading 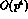 corrections in the
corrections in the 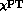 expansion,
a considerable number of such constants are needed. Fortunately, this number is
limited enough for the scheme to remain predictive, and to be
severely tested by accurate experimental data on
expansion,
a considerable number of such constants are needed. Fortunately, this number is
limited enough for the scheme to remain predictive, and to be
severely tested by accurate experimental data on
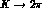 and
and  . In the next section, we briefly review the
application of
. In the next section, we briefly review the
application of  to
to 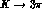 .
.