


Next: 5.2.2 Resonance exchange model
Up: 5.2 Factorization and resonance
Previous: 5.2 Factorization and resonance
A definite prediction for  coupling constants (both strong and weak
ones) can be obtained by using the framework of chiral perturbation theory
in the leading
coupling constants (both strong and weak
ones) can be obtained by using the framework of chiral perturbation theory
in the leading 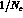 expansion (
expansion ( ) and leading order
) and leading order
 ,
,  being the number of quark colors, combined with
factorization. Basically, noting that the quark effective nonleptonic
Hamiltonian (18) is of the
being the number of quark colors, combined with
factorization. Basically, noting that the quark effective nonleptonic
Hamiltonian (18) is of the  form, in this
approach a `bosonization' prescription is separately applied to each of
the quark currents. For example, the left-handed currents, considered as
Noether currents of the chiral symmetry of the QCD effective action, can
be expanded in
form, in this
approach a `bosonization' prescription is separately applied to each of
the quark currents. For example, the left-handed currents, considered as
Noether currents of the chiral symmetry of the QCD effective action, can
be expanded in  plus
plus 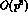 terms as:
terms as:

where  has been defined previously, and
has been defined previously, and 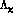 is a scale
characterizing chiral symmetry breaking (of the order of
is a scale
characterizing chiral symmetry breaking (of the order of  ).
An analogous bosonization could be written for right-handed current
operators. Replacing Eq. (36) into the large
).
An analogous bosonization could be written for right-handed current
operators. Replacing Eq. (36) into the large  effective nonleptonic quark Hamiltonian [34], the chiral weak
Lagrangian
effective nonleptonic quark Hamiltonian [34], the chiral weak
Lagrangian  assumes the factorized,
assumes the factorized, 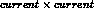 structure [35,36]
structure [35,36]
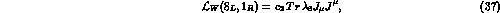
and an analogous expression can be obtained for the 27-plet component.
The advantage of factorization, which is expected to hold in the large  approximation, is
that the strong Lagrangian, via the bosonization prescription
(36) of the chiral quark currents, uniquely determines the structure
of
approximation, is
that the strong Lagrangian, via the bosonization prescription
(36) of the chiral quark currents, uniquely determines the structure
of 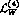 . In particular, the unknown weak counterterms can be
related to (known) strong counterterms. The additional advantage of
the large
. In particular, the unknown weak counterterms can be
related to (known) strong counterterms. The additional advantage of
the large 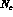 approximation is that, in this limit, the strong coupling
constants can be predicted [37], so that the number of free parameters
is reduced to a minimum. Numerical results in the
approximation is that, in this limit, the strong coupling
constants can be predicted [37], so that the number of free parameters
is reduced to a minimum. Numerical results in the  approach,
from Refs. [35] and [36], are
reported in Tab. 6. The comparison with the data seems encouraging, although,
concerning the test in the
approach,
from Refs. [35] and [36], are
reported in Tab. 6. The comparison with the data seems encouraging, although,
concerning the test in the 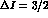 sector and the needed accuracies,
the same comments hold as previously made with regard to
Eqs. (33) and (34).
sector and the needed accuracies,
the same comments hold as previously made with regard to
Eqs. (33) and (34).
Although being quite predictive, the leading 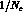 scheme has also some
conceptual difficulties. For example, the results of Tab. 6 are obtained by
employing the values of
scheme has also some
conceptual difficulties. For example, the results of Tab. 6 are obtained by
employing the values of  in Eq. (37), and of the corresponding
27-plet coupling constant
in Eq. (37), and of the corresponding
27-plet coupling constant  , measured from the experimental
, measured from the experimental 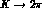 data, instead of taking the (rather different) leading
data, instead of taking the (rather different) leading  values of these
coefficients. This opens the question of the quantitative role of
next-to-leading
values of these
coefficients. This opens the question of the quantitative role of
next-to-leading  corrections and nonfactorizable contributions
[38], and of the convergence of the
expansion for
corrections and nonfactorizable contributions
[38], and of the convergence of the
expansion for 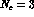 . Another point is that chiral loops are negligible
at the leading order in
. Another point is that chiral loops are negligible
at the leading order in  , hence strong rescattering phases vanish
and must be included by hand. In the absence of meson loops, the counterterm
coupling constants become mass-scale independent, so that the problem of the
, hence strong rescattering phases vanish
and must be included by hand. In the absence of meson loops, the counterterm
coupling constants become mass-scale independent, so that the problem of the
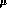 -dependence is not well-addressed and, at this order,
the comparison with the results obtained in the full chiral Lagrangian theory
is not unambiguous.
-dependence is not well-addressed and, at this order,
the comparison with the results obtained in the full chiral Lagrangian theory
is not unambiguous.



Next: 5.2.2 Resonance exchange model
Up: 5.2 Factorization and resonance
Previous: 5.2 Factorization and resonance
Carlos E.Piedrafita
 coupling constants (both strong and weak
ones) can be obtained by using the framework of chiral perturbation theory
in the leading
coupling constants (both strong and weak
ones) can be obtained by using the framework of chiral perturbation theory
in the leading 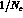 expansion (
expansion ( ) and leading order
) and leading order
 ,
,  being the number of quark colors, combined with
factorization. Basically, noting that the quark effective nonleptonic
Hamiltonian (18) is of the
being the number of quark colors, combined with
factorization. Basically, noting that the quark effective nonleptonic
Hamiltonian (18) is of the  form, in this
approach a `bosonization' prescription is separately applied to each of
the quark currents. For example, the left-handed currents, considered as
Noether currents of the chiral symmetry of the QCD effective action, can
be expanded in
form, in this
approach a `bosonization' prescription is separately applied to each of
the quark currents. For example, the left-handed currents, considered as
Noether currents of the chiral symmetry of the QCD effective action, can
be expanded in  plus
plus 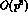 terms as:
terms as:

 has been defined previously, and
has been defined previously, and 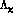 is a scale
characterizing chiral symmetry breaking (of the order of
is a scale
characterizing chiral symmetry breaking (of the order of  ).
An analogous bosonization could be written for right-handed current
operators. Replacing Eq. (
).
An analogous bosonization could be written for right-handed current
operators. Replacing Eq. ( effective nonleptonic quark Hamiltonian [
effective nonleptonic quark Hamiltonian [ assumes the factorized,
assumes the factorized, 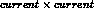 structure [
structure [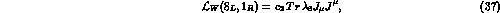
 approximation, is
that the strong Lagrangian, via the bosonization prescription
(
approximation, is
that the strong Lagrangian, via the bosonization prescription
(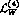 . In particular, the unknown weak counterterms can be
related to (known) strong counterterms. The additional advantage of
the large
. In particular, the unknown weak counterterms can be
related to (known) strong counterterms. The additional advantage of
the large 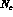 approximation is that, in this limit, the strong coupling
constants can be predicted [
approximation is that, in this limit, the strong coupling
constants can be predicted [ approach,
from Refs. [
approach,
from Refs. [ sector and the needed accuracies,
the same comments hold as previously made with regard to
Eqs. (
sector and the needed accuracies,
the same comments hold as previously made with regard to
Eqs. (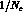 scheme has also some
conceptual difficulties. For example, the results of Tab. 6 are obtained by
employing the values of
scheme has also some
conceptual difficulties. For example, the results of Tab. 6 are obtained by
employing the values of  in Eq. (
in Eq. ( , measured from the experimental
, measured from the experimental 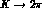 data, instead of taking the (rather different) leading
data, instead of taking the (rather different) leading  values of these
coefficients. This opens the question of the quantitative role of
next-to-leading
values of these
coefficients. This opens the question of the quantitative role of
next-to-leading  corrections and nonfactorizable contributions
[
corrections and nonfactorizable contributions
[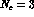 . Another point is that chiral loops are negligible
at the leading order in
. Another point is that chiral loops are negligible
at the leading order in  , hence strong rescattering phases vanish
and must be included by hand. In the absence of meson loops, the counterterm
coupling constants become mass-scale independent, so that the problem of the
, hence strong rescattering phases vanish
and must be included by hand. In the absence of meson loops, the counterterm
coupling constants become mass-scale independent, so that the problem of the
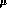 -dependence is not well-addressed and, at this order,
the comparison with the results obtained in the full chiral Lagrangian theory
is not unambiguous.
-dependence is not well-addressed and, at this order,
the comparison with the results obtained in the full chiral Lagrangian theory
is not unambiguous.