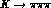Next: 4 Experimental determinations
Up: Chapter 6 Section 1
Previous: 2 Kinematics and Dalitz
Consistent with Eq. (10), also the 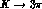 transition
amplitudes are expanded in power series of the variables X and Y around
the centre of the Dalitz plot X=Y=0, assuming the absence of nearby poles,
up to quadratic terms. Limiting to
transition
amplitudes are expanded in power series of the variables X and Y around
the centre of the Dalitz plot X=Y=0, assuming the absence of nearby poles,
up to quadratic terms. Limiting to 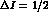 and
and 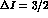 transitions, as also consistent with experimental data, there are three
possible three-pion final states with definite isospin:
transitions, as also consistent with experimental data, there are three
possible three-pion final states with definite isospin:
 ;
; 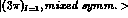 ; and
; and
 . Due to the Bose symmetry of the three-pion final state,
the transition (of the
. Due to the Bose symmetry of the three-pion final state,
the transition (of the  ) to the I=0 state, although possible in
principle, is strongly suppressed by a high angular momentum centrifugal
barrier, and we ignore it. Neglecting isospin breaking effects, the general
Bose-symmetric and CP conserving expansion can be written in terms of five
independent weak amplitudes as [8,9]:
) to the I=0 state, although possible in
principle, is strongly suppressed by a high angular momentum centrifugal
barrier, and we ignore it. Neglecting isospin breaking effects, the general
Bose-symmetric and CP conserving expansion can be written in terms of five
independent weak amplitudes as [8,9]:
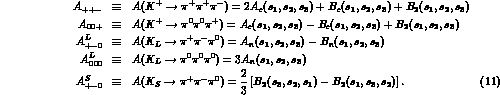
In Eq. (11), 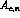 are completely symmetric under permutations
of the indices 1, 2 and 3. Conversely,
are completely symmetric under permutations
of the indices 1, 2 and 3. Conversely, 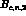 are symmetric only under
the exchange
are symmetric only under
the exchange 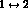 , and under permutations of indices obey
the relation
, and under permutations of indices obey
the relation
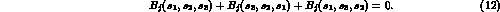
Finally, the amplitude for  is antisymmetric under
the exchange
is antisymmetric under
the exchange 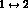 . From the isospin point of view, the
amplitudes
. From the isospin point of view, the
amplitudes 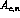 and
and  contribute to
contribute to 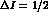 and
and
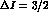 transitions to the I=1 final state, while
transitions to the I=1 final state, while 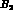 is the pure
is the pure
 transition to I=2. Also, one should notice that there are
two kinds of amplitudes to final I=1, which reflect the different pion
exchange symmetry properties of the corresponding three-pion states, i.e.,
the fully symmetric A's and the B's with mixed symmetry.
transition to I=2. Also, one should notice that there are
two kinds of amplitudes to final I=1, which reflect the different pion
exchange symmetry properties of the corresponding three-pion states, i.e.,
the fully symmetric A's and the B's with mixed symmetry.
Taking the symmetry properties into account, A's and B's
can be expanded up to quadratic terms in X and Y as follows:
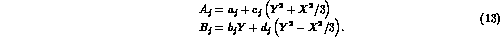
In the absence of final state strong interactions, the CP conserving
amplitudes in (11) and (13) could be taken as real. As
required by unitarity, strong interaction rescattering of final state pions
produce imaginary parts, which can be taken into account by introducing
more phenomenological parameters (in addition to 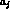 ,
,  ,
,  and
and
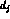 ) in Eq. (13). Due to the smallness of the available
) in Eq. (13). Due to the smallness of the available
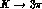 phase space, these effects are expected to be small and, to avoid
too many free parameters, in current fits to the data such strong phases
have been assumed to be negligible (within an uncertainty of
phase space, these effects are expected to be small and, to avoid
too many free parameters, in current fits to the data such strong phases
have been assumed to be negligible (within an uncertainty of  ).
This assumption is consistent with the available experimental
information, and also with theoretical expectations [5,10].
).
This assumption is consistent with the available experimental
information, and also with theoretical expectations [5,10].
Nevertheless, as being sensitive to the properties of low-energy meson
dynamics, rescattering effects are theoretically quite interesting and
could eventually be in the reach of next-generation, high precision
experiments on 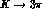 . Consequently, their measurement would provide
alternative, and stringent, tests of the relevant theoretical description.
Specifically, of the pion-pion interaction if one neglects irreducible
. Consequently, their measurement would provide
alternative, and stringent, tests of the relevant theoretical description.
Specifically, of the pion-pion interaction if one neglects irreducible
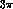 rescattering diagrams that should be phase space-suppressed (barring
anomalously large
rescattering diagrams that should be phase space-suppressed (barring
anomalously large  vertices). Such tests would involve the
really low-energy range, where the framework of chiral perturbation theory
(
vertices). Such tests would involve the
really low-energy range, where the framework of chiral perturbation theory
( ) can be most reliably applied.
Another, and very important, point of interest is the fact that these
imaginary parts crucially enter the determination of direct CP-violating
asymmetries in
) can be most reliably applied.
Another, and very important, point of interest is the fact that these
imaginary parts crucially enter the determination of direct CP-violating
asymmetries in  decays, and consequently are relevant to searches
for this, still unclear, phenomenon in a channel alternative to
decays, and consequently are relevant to searches
for this, still unclear, phenomenon in a channel alternative to
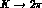 [11].
[11].
Phenomenologically, momentum dependence of rescattering should be taken
into account for a consistent low-energy expansion of the amplitudes. This
is desirable also in view of the momentum expansions predicted
by chiral perturbation theory, which will be described in the sequel.
For the parametrization of such effects, there is the
complication that the two final I=1 three-pion states are coupled by (isospin
conserving) strong interactions, so that they can mix. This situation can be
dealt with, rather generally, by a coupled-channel formalism that introduces,
in the I=1 sector, a two-dimensional, momentum-dependent rescattering
matrix R common to both charged and neutral kaon decays, connecting
symmetric and nonsymmetric amplitudes [12]. Since R=I
corresponds to the limiting case of
no final state interaction, R can be expanded as 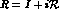 ,
where the elements of the (real) matrix
,
where the elements of the (real) matrix  are functions of X and
Y. Such functions can be expanded around the centre of the Dalitz plot,
similar to Eq. (13), and are expected to be small over the whole
allowed kinematical region. Moreover, in general the R-matrix elements are
not all independent, but are related by unitarity constraints following from
probability conservation.
are functions of X and
Y. Such functions can be expanded around the centre of the Dalitz plot,
similar to Eq. (13), and are expected to be small over the whole
allowed kinematical region. Moreover, in general the R-matrix elements are
not all independent, but are related by unitarity constraints following from
probability conservation.
Contrary to the I=1 case, for the decays to the I=2 three-pion state,
which is unique and cannot mix with the others via strong interactions,
there is just one amplitude with definite symmetry properties, and final state
interactions are simply taken into account by a phase function that is unique
for all decay modes, similar to the case of  where I=0 and I=2
final states do not mix.
where I=0 and I=2
final states do not mix.
For simplicity, one can limit to include rescattering effects only in the
constant and linear slopes in Eq. (13), as it seems justified
by the smallness of experimental quadratic slopes. In
that case, using Eq. (13), the expansion of Eq. (11)
around X=Y=0 takes on the form:
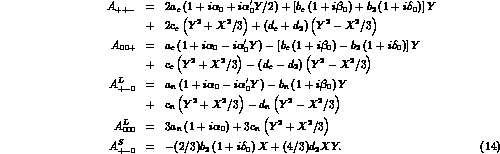
The amplitudes for the decays of the  are determined by taking
complex-conjugates of the coefficients
are determined by taking
complex-conjugates of the coefficients 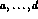 with unchanged strong
interaction imaginary parts. CP conservation implies that these
coefficients should be real and consequently, in this case, the amplitudes
for
with unchanged strong
interaction imaginary parts. CP conservation implies that these
coefficients should be real and consequently, in this case, the amplitudes
for 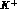 and
and 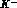 decays must be the same. In the presence of CP violation,
the coefficients
decays must be the same. In the presence of CP violation,
the coefficients 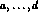 are in general complex, so that amplitudes
for charge-conjugate processes can be different. Furthermore, in this
situation the
are in general complex, so that amplitudes
for charge-conjugate processes can be different. Furthermore, in this
situation the 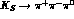 amplitude could get additional,
imaginary constant and linear (in Y) terms, while an imaginary amplitude
linear in X could appear in
amplitude could get additional,
imaginary constant and linear (in Y) terms, while an imaginary amplitude
linear in X could appear in  [13].
[13].
A representation alternative to (14), which has been adopted in
fits to experimental data [5,10], is the expansion in terms of
amplitudes with definite isospin selection rules. With 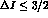 ,
neglecting strong interaction imaginary parts, such an expansion can be
written as
,
neglecting strong interaction imaginary parts, such an expansion can be
written as
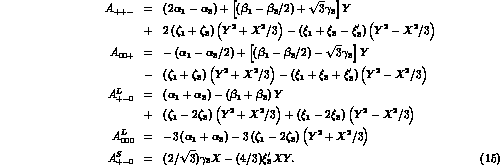
In Eq. (15), the subscripts 1 and 3 refer to 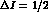 and
and
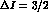 , respectively. The relation between the amplitudes in
Eq. (14) and those in Eq. (15) is easily found to
be:
, respectively. The relation between the amplitudes in
Eq. (14) and those in Eq. (15) is easily found to
be:

In conclusion, the complex of  modes is described by the set
of ten independent (real) isospin amplitudes in Eq. (15),
which are collected in Tab. 3 for convenience, or alternatively by the ten
amplitudes in Eq. (14). There are, in addition, the imaginary
parts from final state strong interactions, parametrized in leading order
by four real constants, as in Eq. (14).
modes is described by the set
of ten independent (real) isospin amplitudes in Eq. (15),
which are collected in Tab. 3 for convenience, or alternatively by the ten
amplitudes in Eq. (14). There are, in addition, the imaginary
parts from final state strong interactions, parametrized in leading order
by four real constants, as in Eq. (14).

Table 3: Independent isospin amplitudes for 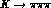



Next: 4 Experimental determinations
Up: Chapter 6 Section 1
Previous: 2 Kinematics and Dalitz
Carlos E.Piedrafita
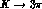 transition
amplitudes are expanded in power series of the variables X and Y around
the centre of the Dalitz plot X=Y=0, assuming the absence of nearby poles,
up to quadratic terms. Limiting to
transition
amplitudes are expanded in power series of the variables X and Y around
the centre of the Dalitz plot X=Y=0, assuming the absence of nearby poles,
up to quadratic terms. Limiting to 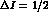 and
and 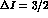 transitions, as also consistent with experimental data, there are three
possible three-pion final states with definite isospin:
transitions, as also consistent with experimental data, there are three
possible three-pion final states with definite isospin:
 ;
; 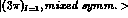 ; and
; and
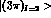 . Due to the Bose symmetry of the three-pion final state,
the transition (of the
. Due to the Bose symmetry of the three-pion final state,
the transition (of the 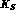 ) to the I=0 state, although possible in
principle, is strongly suppressed by a high angular momentum centrifugal
barrier, and we ignore it. Neglecting isospin breaking effects, the general
Bose-symmetric and CP conserving expansion can be written in terms of five
independent weak amplitudes as [8,9]:
) to the I=0 state, although possible in
principle, is strongly suppressed by a high angular momentum centrifugal
barrier, and we ignore it. Neglecting isospin breaking effects, the general
Bose-symmetric and CP conserving expansion can be written in terms of five
independent weak amplitudes as [8,9]:
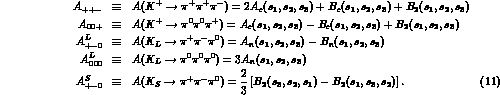
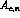 are completely symmetric under permutations
of the indices 1, 2 and 3. Conversely,
are completely symmetric under permutations
of the indices 1, 2 and 3. Conversely, 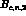 are symmetric only under
the exchange
are symmetric only under
the exchange 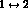 , and under permutations of indices obey
the relation
, and under permutations of indices obey
the relation
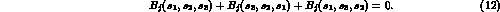
 is antisymmetric under
the exchange
is antisymmetric under
the exchange 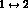 . From the isospin point of view, the
amplitudes
. From the isospin point of view, the
amplitudes 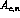 and
and  contribute to
contribute to 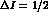 and
and
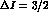 transitions to the I=1 final state, while
transitions to the I=1 final state, while 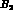 is the pure
is the pure
 transition to I=2. Also, one should notice that there are
two kinds of amplitudes to final I=1, which reflect the different pion
exchange symmetry properties of the corresponding three-pion states, i.e.,
the fully symmetric A's and the B's with mixed symmetry.
transition to I=2. Also, one should notice that there are
two kinds of amplitudes to final I=1, which reflect the different pion
exchange symmetry properties of the corresponding three-pion states, i.e.,
the fully symmetric A's and the B's with mixed symmetry.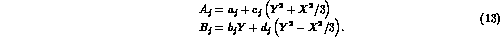
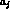 ,
,  ,
,  and
and
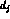 ) in Eq. (
) in Eq. (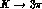 phase space, these effects are expected to be small and, to avoid
too many free parameters, in current fits to the data such strong phases
have been assumed to be negligible (within an uncertainty of
phase space, these effects are expected to be small and, to avoid
too many free parameters, in current fits to the data such strong phases
have been assumed to be negligible (within an uncertainty of  ).
This assumption is consistent with the available experimental
information, and also with theoretical expectations [
).
This assumption is consistent with the available experimental
information, and also with theoretical expectations [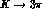 . Consequently, their measurement would provide
alternative, and stringent, tests of the relevant theoretical description.
Specifically, of the pion-pion interaction if one neglects irreducible
. Consequently, their measurement would provide
alternative, and stringent, tests of the relevant theoretical description.
Specifically, of the pion-pion interaction if one neglects irreducible
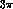 rescattering diagrams that should be phase space-suppressed (barring
anomalously large
rescattering diagrams that should be phase space-suppressed (barring
anomalously large  vertices). Such tests would involve the
really low-energy range, where the framework of chiral perturbation theory
(
vertices). Such tests would involve the
really low-energy range, where the framework of chiral perturbation theory
( ) can be most reliably applied.
Another, and very important, point of interest is the fact that these
imaginary parts crucially enter the determination of direct CP-violating
asymmetries in
) can be most reliably applied.
Another, and very important, point of interest is the fact that these
imaginary parts crucially enter the determination of direct CP-violating
asymmetries in  decays, and consequently are relevant to searches
for this, still unclear, phenomenon in a channel alternative to
decays, and consequently are relevant to searches
for this, still unclear, phenomenon in a channel alternative to
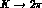 [
[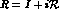 ,
where the elements of the (real) matrix
,
where the elements of the (real) matrix  are functions of X and
Y. Such functions can be expanded around the centre of the Dalitz plot,
similar to Eq. (
are functions of X and
Y. Such functions can be expanded around the centre of the Dalitz plot,
similar to Eq. ( where I=0 and I=2
final states do not mix.
where I=0 and I=2
final states do not mix.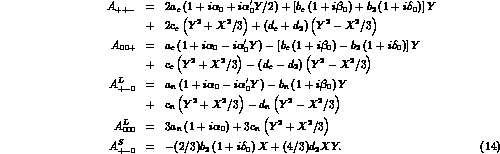
 are determined by taking
complex-conjugates of the coefficients
are determined by taking
complex-conjugates of the coefficients 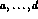 with unchanged strong
interaction imaginary parts. CP conservation implies that these
coefficients should be real and consequently, in this case, the amplitudes
for
with unchanged strong
interaction imaginary parts. CP conservation implies that these
coefficients should be real and consequently, in this case, the amplitudes
for 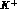 and
and 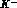 decays must be the same. In the presence of CP violation,
the coefficients
decays must be the same. In the presence of CP violation,
the coefficients 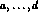 are in general complex, so that amplitudes
for charge-conjugate processes can be different. Furthermore, in this
situation the
are in general complex, so that amplitudes
for charge-conjugate processes can be different. Furthermore, in this
situation the 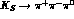 amplitude could get additional,
imaginary constant and linear (in Y) terms, while an imaginary amplitude
linear in X could appear in
amplitude could get additional,
imaginary constant and linear (in Y) terms, while an imaginary amplitude
linear in X could appear in  [
[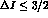 ,
neglecting strong interaction imaginary parts, such an expansion can be
written as
,
neglecting strong interaction imaginary parts, such an expansion can be
written as
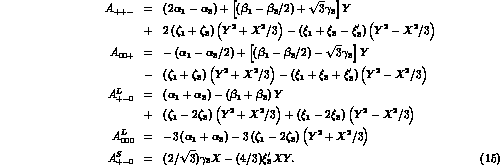
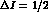 and
and
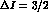 , respectively. The relation between the amplitudes in
Eq. (
, respectively. The relation between the amplitudes in
Eq. (
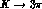 modes is described by the set
of ten independent (real) isospin amplitudes in Eq. (
modes is described by the set
of ten independent (real) isospin amplitudes in Eq. (