For the transition
one can define the following kinematical invariants:
where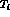 
are the pion kinetic energies in the kaon rest frame:
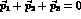and 
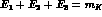. Since
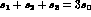with 
,
there are only two independent kinematical variables, which can be defined as
Here, `3' indicates, for a given decay channel, the `odd charge' pion. We are neglecting pion (and kaon) mass differences, except in the Q-values, that significantly depend on them:
and, with an obvious notation referring to the charges of final pion states:
In practice, to determine the transition amplitudes from the experimental analysis, in addition to using correct pion and kaon masses, one must account also for isospin breaking and QED corrections.
The Dalitz plot for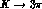 
is the equilateral triangle with
height Q shown in Fig. 1, where the perpendiculars from internal
points (representing the events) to the sides determine the pion kinetic
energies, obviously satisfying the energy conservation Eq. (4).
Conventionally, the vertical perpendicular refers to the `odd charge' pion.
The centre of the diagram, representing the origin of the three axes at
along which one plots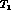 
, 
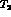and 
, corresponds to
the symmetric point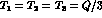 
. Cartesian coordinates of a point
relative to this origin are easily seen to be proportional to
the values of Y and of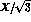 
, respectively. All points inside the
indicated boundary contour (resulting from three-momentum conservation)
are kinematically allowed and represent possible decay events. The diagram
is divided into `sextants', labeled from I to VI, which under permutations of
indistinguishable pions are permuted into each other by reflections in the
corresponding triangle median.
To evaluate phase space integrals, it is often useful to define Dalitz
variables by expressing kinetic energies
in terms of polar coordinates r and 
, with the origin at the symmetric
point [6]:
In Eq. (6):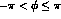 
and 
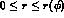, with
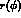the boundary curve in the Dalitz plot, implicitly defined, for
equal pion masses, by the equation
with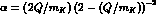 
.
In the approximation of neglecting 
, which actually is of the order
of 
, the limiting curve in the plot would become a circle. Moreover,
the variables X and Y defined in (3) are expressed in
terms of polar coordinates as
so that the plot in terms of Y and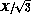 
is quite similar to
Fig. 1 (except from the maximum radius of the contour of the allowed
region, which in this case is obviously different).
The decay rates are expressed in terms of polar variables as
where the integration is over the full Dalitz plot. Such integration, as
well as integrations over the Dalitz plot with cuts, becomes particularly
simple in the limit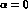 
in (7), which in many cases
represents a good approximation. Explicit calculations of a set of relevant
Dalitz plot integrals, also with cuts, can be found in the Appendix of
Ref. [7].
Since the maximum allowed pion kinetic energies are rather small
(
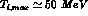), it is natural to expand Dalitz plot
distributions in powers of Y and X:
where, actually, CP conservation implies j=0. The experimental data
do not require higher powers than included in (10), and the
determinations of 
, g, h and k for the different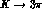 
modes are listed in Tab. 2.
As one can see, present accuracies are at % level or better (depending on
the different decay channels) for the widths 
and the linear slopes
g, but are somewhat worse (in general much larger than 10%) for the
quadratic slopes h and k.
Table 2: Experimental values of widths and Dalitz plot slopes for
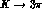[1].
.
