


Next: References
Up: Chapter 6 Section 1
Previous: 5.2.2 Resonance exchange model
According to the previous considerations, accurate measurements of the
 Dalitz plot for the individual channels would allow a stringent
test of the current theoretical description of the
Dalitz plot for the individual channels would allow a stringent
test of the current theoretical description of the
 nonleptonic weak interaction, in particular of the
chiral Lagrangian realization to order
nonleptonic weak interaction, in particular of the
chiral Lagrangian realization to order  . The determination of isospin
amplitudes requires, in general, the combination of data on both
. The determination of isospin
amplitudes requires, in general, the combination of data on both 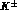 and
and
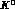 decays. DA
decays. DA NE is a source of pure kaon beams, free from background
contaminations, which in principle should allow high statistical accuracy
(see Tab. 1), provided that detection efficiencies for decay products are also
high. However, in some cases the present experimental accuracy is mostly
limited by systematic errors that must be decreased accordingly, in order
to take advantage of the quality of kaon beams. Another source of
difficulty, to be taken into account in
NE is a source of pure kaon beams, free from background
contaminations, which in principle should allow high statistical accuracy
(see Tab. 1), provided that detection efficiencies for decay products are also
high. However, in some cases the present experimental accuracy is mostly
limited by systematic errors that must be decreased accordingly, in order
to take advantage of the quality of kaon beams. Another source of
difficulty, to be taken into account in 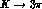 analyses, is the
correlations among, e.g., linear and quadratic Dalitz plot slopes, which
relate the accuracies obtainable for these parameters. The case of
analyses, is the
correlations among, e.g., linear and quadratic Dalitz plot slopes, which
relate the accuracies obtainable for these parameters. The case of
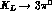 is a special one, since the quadratic slope
is not contaminated by the linear amplitude which is zero for this mode
(see Eq. (14)), and electromagnetic corrections are not
required.
is a special one, since the quadratic slope
is not contaminated by the linear amplitude which is zero for this mode
(see Eq. (14)), and electromagnetic corrections are not
required.
The direct observation of many hundreds of  decay
events, with practically no background (see Tab. 1), should represent a
significant achievement obtainable at DA
decay
events, with practically no background (see Tab. 1), should represent a
significant achievement obtainable at DA NE and, as pointed out
previously, will allow to carefully test the
NE and, as pointed out
previously, will allow to carefully test the 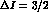 component of the
weak Hamiltonian.
component of the
weak Hamiltonian.
Another interesting analysis of  is suggested
by the use of DA
is suggested
by the use of DA NE as an `interferometer', where the time dependence
of
NE as an `interferometer', where the time dependence
of  -
- interference in vacuum can be accurately studied. Since the
initial
interference in vacuum can be accurately studied. Since the
initial  state from
state from  decay is the antisymmetric superposition
decay is the antisymmetric superposition
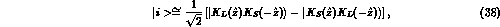
where  is the direction of the kaons momenta in the c.m.
system, the subsequent
is the direction of the kaons momenta in the c.m.
system, the subsequent 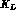 and
and  decays are correlated, and their
quantum interferences show up in relative time distributions and time
asymmetries, which are of great interest in order to test CP (and CPT)
violation [44]. In addition, as an alternative to the direct
observation, also the CP conserving
decays are correlated, and their
quantum interferences show up in relative time distributions and time
asymmetries, which are of great interest in order to test CP (and CPT)
violation [44]. In addition, as an alternative to the direct
observation, also the CP conserving  amplitude and the final state interaction imaginary parts could be
measured via the time dependent interference of this decay with
amplitude and the final state interaction imaginary parts could be
measured via the time dependent interference of this decay with
 [45,12].
[45,12].
Specifically, a convenient observable is represented by
the transition rate for the initial state  to decay into the
final states
to decay into the
final states  at time
at time  and
and
 at time
at time  , respectively (in the following,
, respectively (in the following,
 and
and  are understood to be the proper times). Defining the
`intensity' of time correlated
events
are understood to be the proper times). Defining the
`intensity' of time correlated
events  as:
as:

where  and t is the time difference
and t is the time difference  , making use
of the exponential time-dependence of the mass eigenstates K
, making use
of the exponential time-dependence of the mass eigenstates K and K
and K ,
and integrating over the
,
and integrating over the  phase space, one easily finds,
with the notations
phase space, one easily finds,
with the notations  :
:

and

In Eqs. (40) and (41), 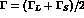 ,
,
 , and for the
, and for the  amplitudes the expansions
(14) or (15) must be introduced.
>From these equations one can notice the possibility to study, in general,
also negative `times', which is peculiar of the
amplitudes the expansions
(14) or (15) must be introduced.
>From these equations one can notice the possibility to study, in general,
also negative `times', which is peculiar of the  factory
[46].
factory
[46].
An important aspect of the interference in (40) and (41) is
that, besides the real parts, the (expectedly) small final state interaction
imaginary parts appear linearly. Instead, the width depends quadratically on
them and thus has less sensitivity to such effects. Accordingly,
by a fit to the full t-dependence of the interference, both the real and the
imaginary parts could be determined (or at least, for the latter ones, a
significant upper bound could be obtained, depending on the available
statistics). This would be a desirable achievement, in view of the discussion
in Sec. 3.
Using Eq. (14) or (15), the interference terms are
easily seen to drop from the intensities (40) and (41)
integrated over the full  Dalitz plot, giving the total
event rates. Considering that in the CP conserving case the Dalitz plot
distributions are even in X for all channels, the interference can be
extracted by integrating the intensities (40) and (41)
over the
Dalitz plot, giving the total
event rates. Considering that in the CP conserving case the Dalitz plot
distributions are even in X for all channels, the interference can be
extracted by integrating the intensities (40) and (41)
over the  phase space with odd-X cuts.
phase space with odd-X cuts.
For example, with  the phase space element, one can define the
asymmetries
the phase space element, one can define the
asymmetries

and

Using Eq. (14) to expand
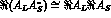 and
and
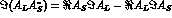 up to second order in
the kinematical variables, one finds to a good approximation
up to second order in
the kinematical variables, one finds to a good approximation

where
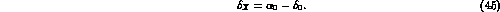
The amplitude  (and
(and  ) can be measured from the rates.
Therefore, Eq. (44) shows that the separate determination of the
) can be measured from the rates.
Therefore, Eq. (44) shows that the separate determination of the
 and
and 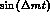 dependences
allows the measurement of the
dependences
allows the measurement of the  amplitude
amplitude  , as well
as of the rescattering relative phase
, as well
as of the rescattering relative phase  . In particular,
the leading order
. In particular,
the leading order  predictions in Eq. (35)
indicate
predictions in Eq. (35)
indicate  .
.
The expression for  is directly obtained from (44)
by the changes
is directly obtained from (44)
by the changes  ,
,  and
and
 but, as a function of time, the
denominator would quickly become large and suppress the interference.
but, as a function of time, the
denominator would quickly become large and suppress the interference.
Analogously, 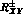 is given by the more complicated expression:
is given by the more complicated expression:
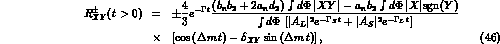
where

and

If separately determined, the coefficients of the
 and
and 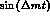 terms
could be useful to constrain the value of the quadratic amplitude
terms
could be useful to constrain the value of the quadratic amplitude  and the combination of imaginary parts in (47). In this regard,
we can notice that the expectedly small
and the combination of imaginary parts in (47). In this regard,
we can notice that the expectedly small 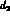 has a large coefficient
proportional to
has a large coefficient
proportional to  (see Tab. 4). In fact, to leading order in
(see Tab. 4). In fact, to leading order in
 , the numerator in Eq. (47) must be of order
, the numerator in Eq. (47) must be of order  (the same counting applies to
(the same counting applies to 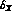 ),
so that for theoretical consistency
),
so that for theoretical consistency  , which is of order
, which is of order 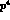 , should
not be included. In that case, Eq. (47) simplifies considerably,
and using Eq. (35) we would predict
, should
not be included. In that case, Eq. (47) simplifies considerably,
and using Eq. (35) we would predict  [12].
[12].
In conclusion, studies of the time-dependent interference described above
should provide alternative measurements of the CP conserving  amplitude, and eventually could also give indications on rescattering
phases and test the relevant predictions. A quantitative discussion for
DA
amplitude, and eventually could also give indications on rescattering
phases and test the relevant predictions. A quantitative discussion for
DA NE, taking into account also the background from the CP even
(
NE, taking into account also the background from the CP even
( ) state due to the radiative decay
) state due to the radiative decay
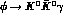 , is presented in Ref. [44].
, is presented in Ref. [44].



Next: References
Up: Chapter 6 Section 1
Previous: 5.2.2 Resonance exchange model
Carlos E.Piedrafita
 Dalitz plot for the individual channels would allow a stringent
test of the current theoretical description of the
Dalitz plot for the individual channels would allow a stringent
test of the current theoretical description of the
 nonleptonic weak interaction, in particular of the
chiral Lagrangian realization to order
nonleptonic weak interaction, in particular of the
chiral Lagrangian realization to order  . The determination of isospin
amplitudes requires, in general, the combination of data on both
. The determination of isospin
amplitudes requires, in general, the combination of data on both 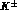 and
and
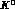 decays. DA
decays. DA NE is a source of pure kaon beams, free from background
contaminations, which in principle should allow high statistical accuracy
(see Tab. 1), provided that detection efficiencies for decay products are also
high. However, in some cases the present experimental accuracy is mostly
limited by systematic errors that must be decreased accordingly, in order
to take advantage of the quality of kaon beams. Another source of
difficulty, to be taken into account in
NE is a source of pure kaon beams, free from background
contaminations, which in principle should allow high statistical accuracy
(see Tab. 1), provided that detection efficiencies for decay products are also
high. However, in some cases the present experimental accuracy is mostly
limited by systematic errors that must be decreased accordingly, in order
to take advantage of the quality of kaon beams. Another source of
difficulty, to be taken into account in 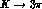 analyses, is the
correlations among, e.g., linear and quadratic Dalitz plot slopes, which
relate the accuracies obtainable for these parameters. The case of
analyses, is the
correlations among, e.g., linear and quadratic Dalitz plot slopes, which
relate the accuracies obtainable for these parameters. The case of
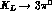 is a special one, since the quadratic slope
is not contaminated by the linear amplitude which is zero for this mode
(see Eq. (14)), and electromagnetic corrections are not
required.
is a special one, since the quadratic slope
is not contaminated by the linear amplitude which is zero for this mode
(see Eq. (14)), and electromagnetic corrections are not
required. decay
events, with practically no background (see Tab. 1), should represent a
significant achievement obtainable at DA
decay
events, with practically no background (see Tab. 1), should represent a
significant achievement obtainable at DA NE and, as pointed out
previously, will allow to carefully test the
NE and, as pointed out
previously, will allow to carefully test the 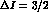 component of the
weak Hamiltonian.
component of the
weak Hamiltonian. is suggested
by the use of DA
is suggested
by the use of DA NE as an `interferometer', where the time dependence
of
NE as an `interferometer', where the time dependence
of  -
- interference in vacuum can be accurately studied. Since the
initial
interference in vacuum can be accurately studied. Since the
initial  state from
state from  decay is the antisymmetric superposition
decay is the antisymmetric superposition
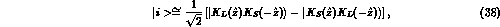
 is the direction of the kaons momenta in the c.m.
system, the subsequent
is the direction of the kaons momenta in the c.m.
system, the subsequent 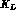 and
and  decays are correlated, and their
quantum interferences show up in relative time distributions and time
asymmetries, which are of great interest in order to test CP (and CPT)
violation [
decays are correlated, and their
quantum interferences show up in relative time distributions and time
asymmetries, which are of great interest in order to test CP (and CPT)
violation [ amplitude and the final state interaction imaginary parts could be
measured via the time dependent interference of this decay with
amplitude and the final state interaction imaginary parts could be
measured via the time dependent interference of this decay with
 [
[ to decay into the
final states
to decay into the
final states  at time
at time  and
and
 at time
at time  , respectively (in the following,
, respectively (in the following,
 and
and  are understood to be the proper times). Defining the
`intensity' of time correlated
events
are understood to be the proper times). Defining the
`intensity' of time correlated
events  as:
as:

 and t is the time difference
and t is the time difference  , making use
of the exponential time-dependence of the mass eigenstates K
, making use
of the exponential time-dependence of the mass eigenstates K and K
and K ,
and integrating over the
,
and integrating over the  phase space, one easily finds,
with the notations
phase space, one easily finds,
with the notations  :
:


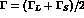 ,
,
 , and for the
, and for the  amplitudes the expansions
(
amplitudes the expansions
( factory
[
factory
[ Dalitz plot, giving the total
event rates. Considering that in the CP conserving case the Dalitz plot
distributions are even in X for all channels, the interference can be
extracted by integrating the intensities (
Dalitz plot, giving the total
event rates. Considering that in the CP conserving case the Dalitz plot
distributions are even in X for all channels, the interference can be
extracted by integrating the intensities ( phase space with odd-X cuts.
phase space with odd-X cuts. the phase space element, one can define the
asymmetries
the phase space element, one can define the
asymmetries


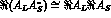 and
and
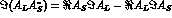 up to second order in
the kinematical variables, one finds to a good approximation
up to second order in
the kinematical variables, one finds to a good approximation

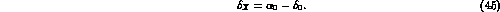
 (and
(and  ) can be measured from the rates.
Therefore, Eq. (
) can be measured from the rates.
Therefore, Eq. ( and
and 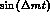 dependences
allows the measurement of the
dependences
allows the measurement of the  amplitude
amplitude  , as well
as of the rescattering relative phase
, as well
as of the rescattering relative phase  . In particular,
the leading order
. In particular,
the leading order  predictions in Eq. (
predictions in Eq. ( .
.  is directly obtained from (
is directly obtained from ( ,
,  and
and
 but, as a function of time, the
denominator would quickly become large and suppress the interference.
but, as a function of time, the
denominator would quickly become large and suppress the interference.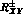 is given by the more complicated expression:
is given by the more complicated expression:
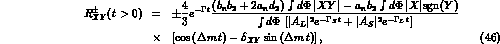


 and
and 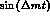 terms
could be useful to constrain the value of the quadratic amplitude
terms
could be useful to constrain the value of the quadratic amplitude  and the combination of imaginary parts in (
and the combination of imaginary parts in (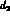 has a large coefficient
proportional to
has a large coefficient
proportional to  (see Tab. 4). In fact, to leading order in
(see Tab. 4). In fact, to leading order in
 , the numerator in Eq. (
, the numerator in Eq. ( (the same counting applies to
(the same counting applies to 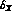 ),
so that for theoretical consistency
),
so that for theoretical consistency  , which is of order
, which is of order 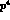 , should
not be included. In that case, Eq. (
, should
not be included. In that case, Eq. ( [
[ amplitude, and eventually could also give indications on rescattering
phases and test the relevant predictions. A quantitative discussion for
DA
amplitude, and eventually could also give indications on rescattering
phases and test the relevant predictions. A quantitative discussion for
DA NE, taking into account also the background from the CP even
(
NE, taking into account also the background from the CP even
( ) state due to the radiative decay
) state due to the radiative decay
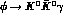 , is presented in Ref. [
, is presented in Ref. [