In the past Sections we have already pointed out that the dynamic of an hypernucleus is essentially ruled by the following facts:
i) the 
is not Pauli-blocked,
ii) the 
experiences an interaction with the nucleons appreciably
weaker than the N-N force.
Point ii) is to a substantial extent related to the zero isospin of the
, which prevents the latter from exchanging
an isovector meson, like the pion or the rho, with a nucleon and bears
relevant implications.
Indeed the relative weakness of the 
-N interaction entails, as it was
already observed, that
the shell structure is not disrupted by the
insertion of the 
into a nucleus and that the mean field binding
the 
is not as deep as the one binding the nucleon.
Moreover, and importantly, the lack of a strong
tensor component, largely carried by the pion and the rho in the
-N interaction, might render the
spin-orbit central potential in the hypernuclei very weak.
And in fact the spectrum of 
,
shown in Fig.3, is consistent with an energy difference of less
than 0.3 MeV between the spin-orbit partners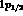 
and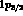 
.
Thus the conjecture that the strong one--body spin--orbit potential,
which is the central element for obtaining the proper organization of the
shells in normal nuclei, is actually due to the two--body tensor force,
is significantly supported by the experimental findings in hypernuclei.
An alternative explanation for the puny spin-orbit mean field in
hypernuclei may come from the recognition that in the
constituent quark model the u and d quarks in the 
are coupled to
zero angular momentum: hence the spin of the 
appears to be carried by
the s quark alone. One could accordingly conjecture that the latter is rather
inert as far as the interaction with the other quarks is concerned.
This explanation needs further elaboration in view of the recent
experiments on the spin structure of the nucleon.
Although two examples have already been provided concerning the survival of the shell structure (Figs. 3 and 4) in a hypernucleus yet the spectrum of the Yttrium (Z=40) displays the pattern of the single particle levels so strikingly that it is still worth to be shown (Fig.5). Especially because it is the heaviest among the hypernuclei till now explored where the shells are so neatly seen. It is obtained via the reaction
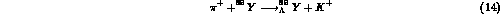
at an incident pion momentum of 1.05 GeV/c and for a scattering angle
.
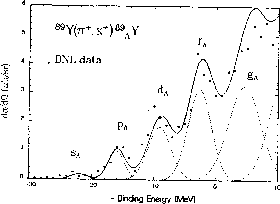
Figure 5: The excitation spectrum for the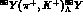 
reaction at 1.05 GeV/c and 
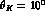. Solid line: a theoretical
calculation. Dotted line: the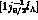 
contributions (from
ref.[15]).
Again the hypernuclear states show up as prominent peaks appearing in the
spectrum.
They belong to the configuration having a neutron hole in the
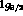single particle level and the 
in all the orbits
starting from the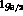 
down to the 
. We thus see
that the 
indeed sits in the inner s-level when the hypernucleus
is in its ground state.
As previously discussed this occurrence accounts for the lack of saturation
experimentally
found in the 
binding energy. The latter is displayed in Fig.6,
which complements the data quoted in Table 1, as a function of
. The power of A should in fact correspond to the next to the
leading
term in the expansion of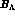 
(here defined as a positive quantity)
in terms of the mass number A. Physically it mainly represents a kinetic
energy correction (see(4)) to the bulk value of the 
binding energy.
One can thus write
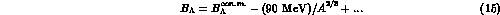
where the coefficient just provides a reasonable fit and the infinite nuclear
matter value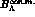 
= 27 MeV
is obtained in a relativistic mean field theory. Its difference from the
corresponding quantity for a nucleon in ordinary nuclear matter, namely
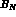=16 MeV, is clearly due to the kinetic energy.
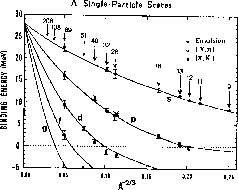
Figure 6: The observed binding energies of 
single--particle states.
The curves correspond to a calculation with an adjusted density--dependent
non--local interaction (from ref.[15]).
In Fig.6 it is indeed
observed that for the available data, which end at the hypernucleus
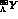, the heavier the hypernucleus, the larger the binding energy.
Also shown in the Figure is the behaviour with A of the energies of the
excited states of the hypernuclei
corresponding to configurations with a 
sitting in the various
shell
model orbits, as previously discussed: thus a family of curves, one for each
single particle level, shows up,
all of them converging to the nuclear matter value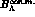 
.
They are calculated starting
from a Woods--Saxon potential well, namely
with
and no spin-orbit potential.
Although the curves appear to nicely fit the available experimental data, a
closer
scrutiny reveals that some amount of non--locality is actually required in the
binding potential.
Clearly the Woods-Saxon well above referred to is only meant to
phenomenologically represent the mean field acting on a 
in a hypernucleus.
It is of significance
that while the radius R and the surface thickness of (17) are close
to the values characterizing the shell model potential of the
S=0 nuclei, its depth is about one third less. In this connection
it should also be mentioned that the binding energy of the 
is presently not understood.
This might suggest, in line with the previous considerations on the
spin-orbit term, that the s quark inside a 
interacts
only very weakly with the u and d quarks of the other nucleons.
In fact such a conjecture would also account for the value of about 27 MeV
above quoted for
, which is in fact roughly two third of the
potential energy per nucleon (about 40 MeV) in infinite nuclear matter
( we have seen that a 
implanted in nuclear matter would have
essentially no kinetic energy).
Another feature of relevance in the hypernuclear structure relates
to the nature of the single particle states of the 
. These appear
to experience
little, if any at all, fragmentation, even the deeply bound ones.
However one must recall that the energy resolution involved in this
experiment is several MeV so that no conclusions can be drawn at
present time.
In accord with the above is the analysis of the dynamical behaviour
of the hypernuclei, in the energy regime above the 
emission
threshold, carried out in terms of a 
-nucleus optical potential.
The real part of the latter has in fact been found to be positive and about
30 MeV strong, whereas the strength of the negative imaginary part does not
exceed a couple of MeV, much less that the corresponding quantity
experienced by a nucleon.
This remarkable stability of the single particle quantum states of the
in the mean field generated by the nuclear medium is indeed
remarkable and worth to be explored in the appropriate theoretical
framework. In fact the above discussed Wood--Saxon phenomenological
potential should actually be obtained through a Hartree calculation starting
from some realistic 
-N interaction.
In this connection if is worth noticing that a 
, implanted
into a nucleus, not only feels the Hartree field generated by its own
interaction with all the other nucleons, but in turn affects the
Hartree--Fock field felt individually by each nucleon. In this perspective
the Hartree--Fock problem acquires a new dimension in hypernuclei.
Formally this can be stated by saying that the two one--body hamiltonian
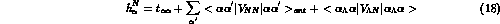
and
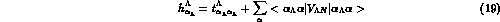
should be self--consistently dealt with simultaneously.
Some estimates of the impact of the 
on the HF mean field
acting on a nucleon predict a change in the single particle energies
as large as 
MeV for the deeply bound nucleons and of about one MeV
for valence nucleons. No experimental evidence for this effect is
presently available. This is unfortunate because it has been argued
[8] that a partial deconfinement of the quarks inside the
could be reflected by a wide spacing, say 5 MeV, among the
most bound single particle levels inside a heavy
hypernucleus like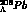 
.
Concerning the two--body force to be utilized as a input the HF
framework it should be observed that in hypernuclear
physics a new self--consistency requirement, to be added to the usual one,
is met at a deeper level in the sense that the two nucleon--nucleon
(
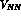) and 
--nucleon (
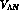) interactions are clearly
interrelated.
One of the few approaches dovetailed to deal with this difficulty has
been carried out
by Nagels et al.[9] starting from the so--called Nijmegen OBE
(one boson exchange) NN potential, specifically designed to account for
the NN scattering data. These authors then solve the associated
Bethe--Goldstone equation for the 
--N scattering in the medium
thus obtaining a G--matrix, i.e. a density--dependent 
--N interaction.
For conveniency the latter, commonly referred to as the YNG force, has all its components expressed via the combination of three gaussians of different ranges. The YNG potential turns out to have the following structure
i.e. it is made up of a central, spin--orbit, anti spin--orbit and tensor
term. In (20)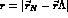 
, 
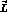is the
relative orbital angular momentum,
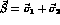the total spin, 
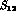the tensor operator and 
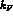the Fermi momentum.
A notable feature of the YNG force, in addition to its rather weak tensor
component, is its strong short range repulsion. The latter is analogous to
the repulsive core of the NN interaction, but has radically different
consequences. In fact when the diagonal matrix elements of the force are
taken with, e.g., the 
--N pair sitting in the configuration
,
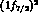then a "repulsive" J=0 matrix element is found to occur (see Fig.7).
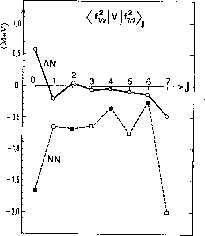
Figure 7: J-dependence of the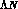 
and NN 
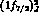diagonal matrix--elements (from ref.[4]).
This "anti--pairing" 
N force is in stunning contrast with the
"attractive" pairing NN potential, which has, as it is well--known,
momentous consequences on the
nuclear dynamics. It reflects a different balance between the short range
repulsion and the intermediate range attraction occurring in the
N channel: indeed a 
can approach more closely a nucleon than
another nucleon can do.
At a more fundamental level attempts have been made to derive the baryon-baryon potential from first principles. One model calculates the effect of the exchange of bosons (OBE). In another the quark-quark force obtained from a one gluon exchange is used in a cluster model. In addition the influence of three-body forces has not been evaluated. A detailed discussion of these attempts would take us too far afield. Suffice to say the fundamental basis of the hyperon-nucleon interaction is still not known.
The YNG potential, as well as others more phenomenological
versions of the 
N interaction, has been extensively applied
to analyze and predict a number of hypernuclear spectra. Since in a
hypernucleus three kinds of particles, the proton, the neutron and the
are coexisting, states characterized by new symmetries should appear.
To display the latter more transparently it is of much convenience to
classify the states according to the 
symmetry.
An often considered
example in this connection is the hypernucleus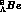 
viewed
as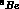 
, whose simple shell model configuration 
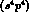belongs to the irreducible representation 
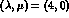of
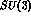with in addition a 
particle.
One thus gets three sets (bands) of states, which with a compact notation can
be labelled as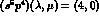 
,
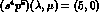and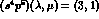 
.
Now the first and third set
are nothing new with respect to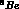 
and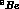 
respectively. But
the second set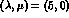 
corresponds to a new symmetry not
found in ordinary nuclei.
Clearly the interest in this type of investigations is partly to search
for states displaying new aspects of symmetry and partly to assess
the amount by which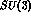 
is broken in hypernuclei.
Are the breakings of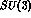 
at the many body level (spectra of hypernuclei)
and at the baryonic level (the octet) related?
It should also be mentioned that along the same lines above outlined
a 
N potential has been derived. Since the experimental
information, not to say the very existence, of the 
hypernuclei
is still somewhat controversial, they will not be discussed here. Suffices it to
say that the mean field acting on a 
appears to be quite shallow,
with a substantial spin--orbit component ( a 
and a nucleon can
exchange a pion or a rho) and the associated states are characterized
by a large width (30 or 40 MeV), mainly associated with the strong decay
channel
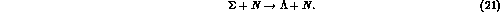
Various mechanisms have been explored that could reduce such a width, like Pauli blocking, dispersion effects, isospin selection rules etc., but the matter appears to be far from being settled.
In concluding this Section a brief reference should be made to hypernuclei
with two 
particles. In principle they can be obtained from a
--hypernucleus formed through the process (9). In fact the 
--hyperon
can interact with a proton inside the nucleus according to
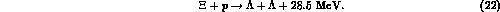
and a double--
hypernucleus can thus be formed with a certain
probability. In practice the data are very scarce.
The importance of double--
hypernuclei relates to a large extent
to the existence and
stability of the H--particle predicted long ago by [10] as a
six--quark bound state exceptionally stable and with a mass about 80 MeV
below the 
decay threshold. The H particle is made up
of two u, d and s quarks coupled to a flavor 
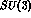singlet and, when
expressed in terms of two baryons configurations, reads
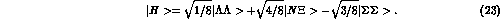
The H particle is still intensively searched for, but has not yet been
convincingly found.
