 --hypernuclei (
--hypernuclei ( ) to normal nuclei (S=0)
occurs through the weak interaction which can change the strangeness.
In contrast to a
) to normal nuclei (S=0)
occurs through the weak interaction which can change the strangeness.
In contrast to a  --hypernucleus a strong decay channel
(
--hypernucleus a strong decay channel
(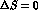 ) is open.
) is open.
The decay of  --hypernuclei (
--hypernuclei ( ) to normal nuclei (S=0)
occurs through the weak interaction which can change the strangeness.
In contrast to a
) to normal nuclei (S=0)
occurs through the weak interaction which can change the strangeness.
In contrast to a  --hypernucleus a strong decay channel
(
--hypernucleus a strong decay channel
(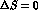 ) is open.
) is open.
The study of the weak decay of a  --hypernucleus aims to the
understanding of the stability of the system on the one side and
of how the many--body nuclear system affects the products of
the
--hypernucleus aims to the
understanding of the stability of the system on the one side and
of how the many--body nuclear system affects the products of
the  decay on the other (clearly the two issues are related).
Moreover the decay process also reflects the influence of
the medium on the
decay on the other (clearly the two issues are related).
Moreover the decay process also reflects the influence of
the medium on the  itself and on the weak interactions it experiences.
itself and on the weak interactions it experiences.
Basically two are the mechanisms for the decay of an hypernucleus:
i) the mesonic decay (for a review see ref. [11]), namely
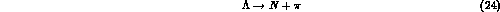
which is just the free decay of the  but now occurring in the medium;
but now occurring in the medium;
ii) the non--mesonic (NM) decay, commonly viewed as being driven by the process
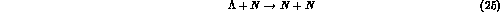
which is only possible in a nucleus.
They are displayed in Fig.8.
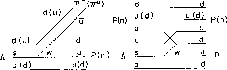
Figure 8: Weak--decay diagrams for mesonic decays (left--hand side), and for
non--mesonic decays (right--hand side) of a  (from ref.[6]).
(from ref.[6]).
For the mesonic decay the following two branches are open in free space
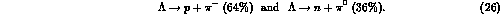
The above branching ratios are in approximate accord with the isospin rule
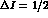 as it can be easily checked with a Clebsch--Gordan analysis.
It is disturbing that such a rule, discovered at the empirical level, has
never been convincingly understood on a sound theoretical ground.
as it can be easily checked with a Clebsch--Gordan analysis.
It is disturbing that such a rule, discovered at the empirical level, has
never been convincingly understood on a sound theoretical ground.
Now, if the process (24), whose Q--value is about 40 MeV (see (2)), occurs
with the  at rest, then most
of the energy is carried away by the pion and it is easily verified that the
outgoing proton remains with only about 5 MeV of energy. Accordingly its
momentum turns out to be
at rest, then most
of the energy is carried away by the pion and it is easily verified that the
outgoing proton remains with only about 5 MeV of energy. Accordingly its
momentum turns out to be
which is much less than the Fermi momentum 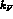 (in the above
(in the above
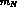 is the nucleon mass). Thus the mesonic decay in nuclei is
substantially hindered by the Pauli principle.
However some high momentum components in the proton wave function are
supplied by the interaction both with the outgoing pion and with the medium:
thus the restriction on the mesonic
is the nucleon mass). Thus the mesonic decay in nuclei is
substantially hindered by the Pauli principle.
However some high momentum components in the proton wave function are
supplied by the interaction both with the outgoing pion and with the medium:
thus the restriction on the mesonic  decay of a hypernucleus is less
severe than implied by (27), even in heavy nuclei, although
the suppression remains impressive.
In this respect the situation is well illustrated in Fig.9.
decay of a hypernucleus is less
severe than implied by (27), even in heavy nuclei, although
the suppression remains impressive.
In this respect the situation is well illustrated in Fig.9.
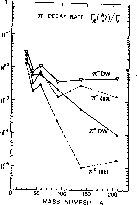
Figure 9: The calculated mesonic decay rates of the free  decay rate
(from ref.[6]).
decay rate
(from ref.[6]).
The NM decay, on the other hand, is not affected by the Pauli blocking. Indeed, assuming the available energy to be equally splitted between the two nucleons, one gets
hence
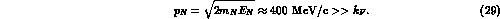
Owing to the large energy and momentum transfer characterizing the
NM decay channel it is clear that the short range component of
the  N interaction is going to play an important role in the
process.
N interaction is going to play an important role in the
process.
Indeed Alberico et al. [12] showed that in nuclear matter the stronger
the  -N short--range repulsion is,
the larger the reduction of the
non--mesonic decay is going to be. This result was achieved by parametrizing
the short range interaction with the Landau--Migdal parameter
-N short--range repulsion is,
the larger the reduction of the
non--mesonic decay is going to be. This result was achieved by parametrizing
the short range interaction with the Landau--Migdal parameter 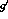 and
allowing for sizable variations of the latter.
and
allowing for sizable variations of the latter.
Central questions to be asked concerning the NM decay of hypernuclei are:
i) how does the NM decay compare with the free  life--time?
life--time?
ii) which of the two mechanisms
and
is more relevant for the NM decay?
iii) how the NM decay is realized in a many--body framework?
Fig.10 provides an answer to the first question: indeed it is clearly seen that
for 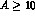 the NM decay mode not only is the dominant one, but also brings
the total width for the decay of a hypernucleus
the NM decay mode not only is the dominant one, but also brings
the total width for the decay of a hypernucleus  back to the free value
back to the free value
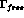 (if not to values larger than
(if not to values larger than  ).
).
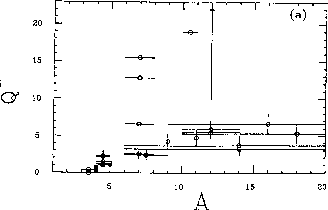
Figure 10: Ratio  of non--mesonic to
of non--mesonic to 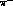 mesonic decay rates as a
function of A.
mesonic decay rates as a
function of A.
Concerning the second question, which of course is not disjoint from the third one, a simple evaluation of Clebsch--Gordan coefficients leads to the geometrical estimate
(of course (32) ignores a 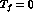 contribution in the denominator).
contribution in the denominator).
The experimental indication, on the other hand, is more consistent with a value for the ratio (32) close to one (although the data are rather scarce).
A variety of calculations have been performed to improve upon the
geometrical estimate. These approaches range from models accounting for
all possible mesons exchanges between 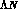 and NN propagation lines
with one strong and one weak vertex to models accounting for the quarks
degrees of freedom. Not surprisingly the results thus obtained show a marked
model dependence.
and NN propagation lines
with one strong and one weak vertex to models accounting for the quarks
degrees of freedom. Not surprisingly the results thus obtained show a marked
model dependence.
This brings us to address the third question, which is more easily answered
in a nuclear matter context. In fact in this framework is transparently
seen that the occurence
of the elementary processes (30) and (31) might be prevented.
Indeed it is easily realized that if the pion emitted from the  ,
an allowed process now since
it is taking place in a weak vertex, is close to the mass--shell ( in the
considered process this correspond to a pion carrying relatively large energy
and little momentum) then it cannot be absorbed by a single nucleon
because, as shown in Fig.11, this would induce a particle--hole excitation
in a region forbidden in nuclear matter. It can do so only when it is
highly virtual (Fig.11).
,
an allowed process now since
it is taking place in a weak vertex, is close to the mass--shell ( in the
considered process this correspond to a pion carrying relatively large energy
and little momentum) then it cannot be absorbed by a single nucleon
because, as shown in Fig.11, this would induce a particle--hole excitation
in a region forbidden in nuclear matter. It can do so only when it is
highly virtual (Fig.11).
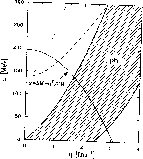
Figure 11: The intersection in the  plane of the parabola
(solid line) representing the energy--momentum relation for the
plane of the parabola
(solid line) representing the energy--momentum relation for the  emitted in
the decay of a
emitted in
the decay of a  at rest with the excitation spectrum of nuclear matter.
Dashed region: particle--hole excitation. Dashed line: the collective pionic
branch. Also shown (dotted line) the free pion branch
(from ref.[12]).
at rest with the excitation spectrum of nuclear matter.
Dashed region: particle--hole excitation. Dashed line: the collective pionic
branch. Also shown (dotted line) the free pion branch
(from ref.[12]).
Therefore a close to the mass--shell pion can only be absorbed by a
pair of nucleons, leading to two particle -- two hole excitations. More
specifically the absorption can occur in the pionic branch, a collective
nuclear state embodying a coherent superposition of pionic and
 --hole elementary excitations, which lies at an energy lower than
the physical pion. Its decay mode in the kinematical region of concern for
the decay of a hypernucleus is by two nucleons emission. It thus appears
that the
--hole elementary excitations, which lies at an energy lower than
the physical pion. Its decay mode in the kinematical region of concern for
the decay of a hypernucleus is by two nucleons emission. It thus appears
that the  decay, particularly in heavy nuclei, is occurring by
a substantial fraction not via the (25), but rather via the process
decay, particularly in heavy nuclei, is occurring by
a substantial fraction not via the (25), but rather via the process
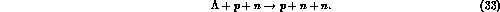
The above outlined situation is somewhat reminiscent of the absorption of a real photon which, even when of relatively high energy, carries nevertheless little momentum and accordingly can only be absorbed on a correlated pair of nucleons (hence the quasi--deuteron model) in order to conserve both energy and momentum. In ref.(11) it is shown that these excitations provide an important contribution to the width for the NM decay.
The identification of the process, because is associated with the emission of three nucleons, poses however a serious experimental challenge.