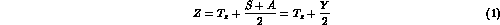
Strangeness has been introduced in particle physics to account for lifetimes in the baryon and meson spectrum much longer (by orders of magnitude) than those expected for strongly interacting systems. Indeed in 1953, Gell-Mann [1] interpreted this experimental finding in terms of selection rules associated with a new (at the time) quantum number, namely the strangeness, S, defined as
in terms of the charge number Z, isospin (third component of) 
and
baryon number A. Alternatively, instead of the strangeness S, one may as
well
consider the hypercharge Y = S + A as indicated in formula (1).
Because of the charge and baryon number conservation, (1) entails the equivalence between isospin and strangeness conservation, a requirement indeed respected by the strong and electromagnetic forces, but violated by the weak interactions, which do not conserve neither T nor S.
As is well-known the introduction of this additional quantum number
allows to classify in a larger scheme based on the unitary symmetry
SU(3), which
encompasses both isospin and strangeness, a new generation of
baryons, i.e. the hyperons, endowed with the strangeness degree of freedom
. Thus in this frame the 
and 
particles, in
addition to
a pair of first generation quarks (namely the u and d) embody as well
a strange
quark s, whereas the 
possesses two strange quarks in addition to a
first generation one.
The stability of the 
particles, which moreover interact with the
protons and neutrons with a force comparable to, although somewhat weaker than
the one acting among the
latter, permits the existence of strange 
nuclei, i.e. hypernuclei.
On the other hand nuclei with an additional 
meson are
not bound since the interaction between a 
and a nucleon is
predominantly repulsive.
Our present knowledge on hypernuclei is limited and cannot be compared with
the one available on conventional nuclei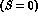 
, yet it has
already provided important clues on nuclear structure; most importantly
it has much broadened the concept of nuclear structure itself.
Since the 
particle, with isospin I=0, strangeness S=-1 and
mass 
=1115.6 MeV, is about 80 MeV lighter than the 
(which also has
S=-1), the most "stable" among the S=-1 hypernuclei are those made up
of nucleons and a 
particle. However because
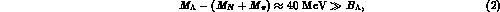
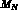and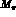 
being the nucleon and the pion mass respectively and
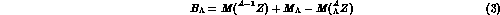
the binding energy of the 
, the hypernucleus will
eventually decay by weak interactions.
Figure 1: Chart of observed 
hypernuclei as of 1988 (from ref.[2]).
Yet it lives long enough to be detected and indeed a number of hypernuclei have been observed: they are shown in Fig.1 and the binding energies of the lighter among them are listed in Table 1.
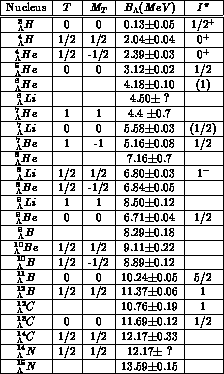
Table 1: The binding energies of some hypernuclei (taken from
ref. [3], p.55 and ref.[4], p.4028). In the second and third columns
are indicated the isospin and its third component.
In the fourth column the binding energy
and in last column the ground state spin and parity, when available,
are quoted.
In this Table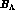 
is seen to be indeed comparable with the
binding energy 
of a nucleon in a S=0 nucleus, but the striking
difference between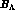 
and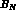 
lies in the fact that the
former grows with the mass number A whereas, as it is well-known,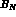 
saturates around a value of about -8 MeV per particle.
This outcome reflects the freedom of the 
to occupy in the host
nucleus orbits which are forbidden to a nucleon since it does not have to
obey to the Pauli principle. In turn the low energy spectrum of a
hypernucleus exhibits new states not present in the normal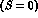 
nuclei.
In this connection Feshbach [2] observes that this might not be exactly
true since the u and d quarks in the nucleon and in the 
have to
satisfy the Pauli principle. Actually, to assess the impact on the
spectra of the hypernuclei of the Pauli principle, which must be
obeyed by the quarks,
will represent a challenging theme of investigation for the
future hypernuclear physics.
Leaving aside this observation a rough estimate of the potential well
binding the 
in a hypernucleus might be obtained by considering the
kinetic energy of a 
particle in the lowest orbit it can occupy in
a "shell model" nucleus, namely the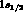 
. One gets
[3]
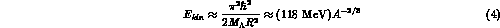
R being the nuclear radius.
For example in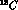 
one has 
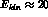MeV. Hence, since
in this nucleus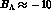 
MeV (see Table 1),
from the relationship
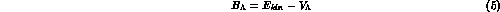
it follows that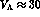 
MeV to be compared with about
55 MeV [5], which is the depth of the potential well felt by
a nucleon in carbon. Of course the
above should only be considered as a rough estimate for the depth of the
well acting on the 
particle in a nucleus. More realistic
evaluations will be later considered.
Concerning the spin and parity assignments in Table II they were obtained
from angular correlations measurements as well as from the determination
of branching ratios for different decays modes (note that to the 
an intrinsic parity +1 is assigned).
