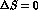 ) one must
necessarily make use of particles (essentially mesons) endowed with strangeness
to produce
) one must
necessarily make use of particles (essentially mesons) endowed with strangeness
to produce 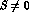 hyperons via strong interactions. The following are
the physical processes commonly considered:
hyperons via strong interactions. The following are
the physical processes commonly considered:
Since the strong interactions conserve strangeness (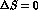 ) one must
necessarily make use of particles (essentially mesons) endowed with strangeness
to produce
) one must
necessarily make use of particles (essentially mesons) endowed with strangeness
to produce 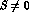 hyperons via strong interactions. The following are
the physical processes commonly considered:
hyperons via strong interactions. The following are
the physical processes commonly considered:
i) reactions where a s quark is exchanged, namely
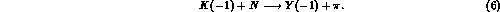
Here the s quark is transferred from a kaon K to a hyperon Y, both
having strangeness S=-1 (in the above N and  represent a
nucleon and pion, respectively).
represent a
nucleon and pion, respectively).
In this reaction the momentum transfer can be quite small. Actually if a
 with a momentum
with a momentum  hits a neutron n at rest, then in the reaction
hits a neutron n at rest, then in the reaction
a "magic" momentum exists such that the  also stays at rest while
the
also stays at rest while
the  moves in the forward direction.
moves in the forward direction.
The equation fixing such a momentum is easily found to be
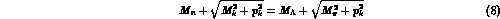
which yields 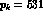 MeV/c.
MeV/c.
If, instead of a  , a
, a  particle is considered one gets
particle is considered one gets
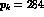 MeV/c.
In Fig.2 the momentum transferred from the kaon to the pion (in the forward
direction) is displayed as a function of the incident kaon momentum.
Note that because of the smallness of the momentum transfer also the
polarization
MeV/c.
In Fig.2 the momentum transferred from the kaon to the pion (in the forward
direction) is displayed as a function of the incident kaon momentum.
Note that because of the smallness of the momentum transfer also the
polarization 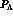 of the
of the  is almost negligible.
On the other hand
for
is almost negligible.
On the other hand
for 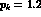 and
and 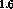 GeV/c it is found that
GeV/c it is found that 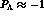 and
and
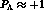 respectively.
respectively.
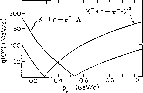
Figure 2: Kinematics of the 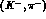 reaction (from ref.[2]).
reaction (from ref.[2]).
ii) Reactions where a 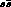 pair is created.
pair is created.
In this instance typical processes are 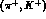 ,
, 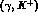 and
and 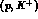 .
Here a s-quark is transferred to a nucleon
yielding an hyperon, whereas the antiquark
.
Here a s-quark is transferred to a nucleon
yielding an hyperon, whereas the antiquark  becomes a constituent
of the final
becomes a constituent
of the final 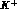 .
.
At variance with the case i) now the momentum transfers are large
(because the final particles, namely the Y and the 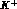 , are heavy):
accordingly the
, are heavy):
accordingly the 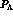 will be large as well.
will be large as well.
iii) Reactions in which the two processes above described are combined into a single one.
Examples of this case are
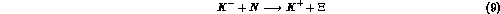
and

where the so-called "cascade particles" 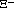 and
and 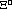 are produced.
are produced.
The reactions we have referred to above are indeed exploited to obtain
hyperons inside nuclei. A number of 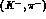 experiments have been performed at CERN and at Brookhaven (BNL).
With the direct
experiments have been performed at CERN and at Brookhaven (BNL).
With the direct  mechanism a neutron can be
replaced with a
mechanism a neutron can be
replaced with a  inside the nucleus so gently that the wave
function of the nuclear system remains essentially unchanged (hence the name
of "substitutional reaction"
for the process). If the pion is emitted in the forward direction
then the angular momentum change occurring in the reaction is
inside the nucleus so gently that the wave
function of the nuclear system remains essentially unchanged (hence the name
of "substitutional reaction"
for the process). If the pion is emitted in the forward direction
then the angular momentum change occurring in the reaction is
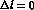 , otherwise
, otherwise 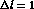 and
and 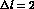 transitions become
possible as well.
transitions become
possible as well.
As an illustration in Fig.3 the spectra of the 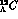 and
and
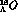 hypernuclei, obtained via the
hypernuclei, obtained via the 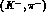 process, are shown.
In both cases it is clearly apparent that when the
process, are shown.
In both cases it is clearly apparent that when the
 particle and the neutron hole, which together identify the
excited state of the hypernuclear system, are in the same single particle orbit
(and coupled to a state of
zero angular momentum and positive parity, i.e.
particle and the neutron hole, which together identify the
excited state of the hypernuclear system, are in the same single particle orbit
(and coupled to a state of
zero angular momentum and positive parity, i.e. 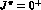 ),
then the corresponding
peak in the cross-section is quite pronounced, whereas for the other
configurations a sizable reduction of the cross-section is seen to occur
(the associated peaks are much less evident).
This finding reflects the marked preference of the
),
then the corresponding
peak in the cross-section is quite pronounced, whereas for the other
configurations a sizable reduction of the cross-section is seen to occur
(the associated peaks are much less evident).
This finding reflects the marked preference of the 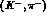 reaction for the
reaction for the 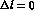 transitions rather than for those having
transitions rather than for those having
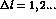 . In turn this explains why the
. In turn this explains why the 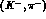 process is not appropriate for exciting low-lying
process is not appropriate for exciting low-lying  hypernuclear
states in heavy nuclei: indeed here the neutron has in general a high
angular momentum thus entailing large
hypernuclear
states in heavy nuclei: indeed here the neutron has in general a high
angular momentum thus entailing large 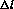 reactions when the
reactions when the
 sits in low lying orbits.
sits in low lying orbits.
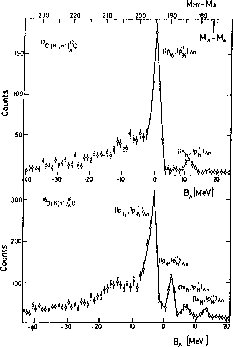
Figure 3: Production of hypernuclei 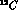 and
and 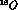 by the
by the
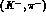 reaction (from ref.[2]).
reaction (from ref.[2]).
For exciting high spin hypernuclear states actually the process
is preferable to (7) (actually (7) and (11) are in fact complementary).
This reaction indeed prefers to create the  in a high angular
momentum state at large excitation energy (quasi-free scattering).
It is, accordingly, well-suited for unfolding the shell
structure of nuclei heavier than those previously considered.
As an example in Fig.4 the
spectrum of the hypernucleus
in a high angular
momentum state at large excitation energy (quasi-free scattering).
It is, accordingly, well-suited for unfolding the shell
structure of nuclei heavier than those previously considered.
As an example in Fig.4 the
spectrum of the hypernucleus 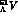 thus obtained is shown.
It is indeed impressive to see in the
figure how the
thus obtained is shown.
It is indeed impressive to see in the
figure how the  is probing all the nuclear shells down to the inner
one, namely the
is probing all the nuclear shells down to the inner
one, namely the 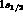 (remember that in
(remember that in 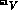 the neutron shells are closed and the
the neutron shells are closed and the 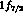 single particle level is
fully occupied).
single particle level is
fully occupied).
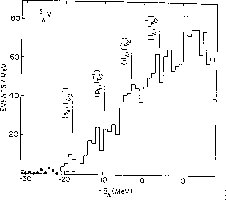
Figure 4: Production of  hypernuclear states in
hypernuclear states in  with the
with the  reaction (from ref.[2]).
reaction (from ref.[2]).
In connection with the reaction (11) it should be observed that the
 , being produced in a high angular momentum state and above its
emission threshold (quasi-free region), may
either escape from the hypernucleus ( with a width
, being produced in a high angular momentum state and above its
emission threshold (quasi-free region), may
either escape from the hypernucleus ( with a width  ) or be
captured inside the hypernucleus (with a width
) or be
captured inside the hypernucleus (with a width 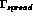 ) where it
spreads its energy with the other constituents. In the latter instance
a compound nucleus is formed eventually decaying by the emission of
several nucleons in addition to a number of
) where it
spreads its energy with the other constituents. In the latter instance
a compound nucleus is formed eventually decaying by the emission of
several nucleons in addition to a number of 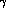 -rays:
at the end of the process a hypernucleus is left
in a variety of quantum states.
-rays:
at the end of the process a hypernucleus is left
in a variety of quantum states.
In the range of excitation energies from 30 to 120 MeV in 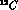 the following value
the following value
has been experimentally found [6]
Now the above energy range is dominated by the quasi-free scattering,
whose cross-section 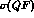 is larger by about two orders of
magnitude than the cross section
is larger by about two orders of
magnitude than the cross section 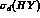 for the formation of an
hypernucleus directly in a bound state,
via, e.g., the process (7). Thus, even by taking the lower value for
the ratio (12), we obtain
for the cross section
for the formation of an
hypernucleus directly in a bound state,
via, e.g., the process (7). Thus, even by taking the lower value for
the ratio (12), we obtain
for the cross section 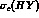 , corresponding to the
formation of an hypernucleus through the compound nucleus mechanism
via (11), the estimate
, corresponding to the
formation of an hypernucleus through the compound nucleus mechanism
via (11), the estimate
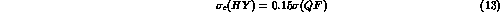
still an order of magnitude larger than 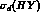 .
.
Due to its importance it is appropriate in conclusion to this Section to
shortly return to consider the
polarization of the  -hypernuclei. It is largely due to the
polarization of the hyperons
produced in the elementary processes like
-hypernuclei. It is largely due to the
polarization of the hyperons
produced in the elementary processes like 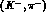 ,
,  ,
,
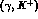 and
and 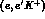 which occurs, as we have already seen,
if the momenta involved are sufficiently
large and reflects the quite significant spin dependence of the
which occurs, as we have already seen,
if the momenta involved are sufficiently
large and reflects the quite significant spin dependence of the
 -N interaction (for example, a notable feature of the latter is that
rather than yielding the strongest attraction
in the triplet state
-N interaction (for example, a notable feature of the latter is that
rather than yielding the strongest attraction
in the triplet state 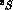 , like the N-N force, appears to be preferring
the singlet state
, like the N-N force, appears to be preferring
the singlet state 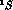 ). However
it is also contributed to by the distortion of the pionic waves
either in the initial or in the final state, which orients the angular
momentum transferred in the reaction.
). However
it is also contributed to by the distortion of the pionic waves
either in the initial or in the final state, which orients the angular
momentum transferred in the reaction.
Estimates of the polarization of the  hypernuclei, obtained through
the
hypernuclei, obtained through
the 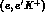 process have been performed since this type of
experiments are expected to be performed at CEBAF. On the other hand the
process have been performed since this type of
experiments are expected to be performed at CEBAF. On the other hand the
 mechanism for obtaining polarized hypernuclei
has been explored by Ejiri [6].
This author considers closed shell nuclei having the lowest
spin--orbit partner filled. As we already know the considered reaction proceeds
primarily through the compound nucleus formation and
the most populated final hypernuclear states, reached at the end of
the statistical decaying process, are those with
a
mechanism for obtaining polarized hypernuclei
has been explored by Ejiri [6].
This author considers closed shell nuclei having the lowest
spin--orbit partner filled. As we already know the considered reaction proceeds
primarily through the compound nucleus formation and
the most populated final hypernuclear states, reached at the end of
the statistical decaying process, are those with
a 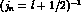 neutron hole and a
neutron hole and a
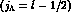
 particle coupled to J=2l.
In other words stretched states with maximum spin are preferentially excited
by the
particle coupled to J=2l.
In other words stretched states with maximum spin are preferentially excited
by the 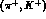 reaction.
Large polarizations of the hypernuclei (of the order of
reaction.
Large polarizations of the hypernuclei (of the order of 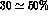 )
are found. The corresponding polarizations of the spin of the
)
are found. The corresponding polarizations of the spin of the  turn out to be of the order of
turn out to be of the order of 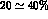 .
.
Another interesting case is provided by the elementary 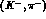 reaction: indeed the latter yields, for momenta larger than 1 GeV/c,
a
reaction: indeed the latter yields, for momenta larger than 1 GeV/c,
a  almost 100
almost 100 polarized [7]. When applied to
populate natural parity states of the hypernucleus
polarized [7]. When applied to
populate natural parity states of the hypernucleus  this
reaction leads to polarizations very small, large and positive and large
and negative for momenta of the incident
this
reaction leads to polarizations very small, large and positive and large
and negative for momenta of the incident  of 0.7, 1.1 and 1.5 GeV/c,
respectively. This shows how sensitive the polarization of an hypernucleus
can be to the kinematics of the reaction selected for its own production.
of 0.7, 1.1 and 1.5 GeV/c,
respectively. This shows how sensitive the polarization of an hypernucleus
can be to the kinematics of the reaction selected for its own production.
Because the produced hypernuclei are polarized, it becomes possible to
measure their magnetic moments. This is an important measurement as it
will test the hypothesis that the hypernucleus consists of a host nucleus
plus a  . One would learn if the hyperon state consists of just a
. One would learn if the hyperon state consists of just a
 or if there is a
or if there is a  component [14].
component [14].