


Next: 5 Summary
Up: Chapter 10 Section 1
Previous: 3 Dispersive Predictions
The polarizabilities --- electric  , magnetic
, magnetic  --- of a
particle, like its charge
radius, reflect its response to an electromagnetic
stimulus [28,21,29].
They are related
to how the Compton amplitudes approach the Born limit at threshold. Thus
the combination
--- of a
particle, like its charge
radius, reflect its response to an electromagnetic
stimulus [28,21,29].
They are related
to how the Compton amplitudes approach the Born limit at threshold. Thus
the combination
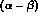 is determined by the slope of the S-wave
is determined by the slope of the S-wave 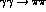 amplitude at the cross-channel threshold :
amplitude at the cross-channel threshold :
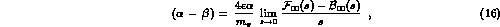
where for the charged pion case  is the one-pion-exchange
Born amplitude,
is the one-pion-exchange
Born amplitude, 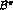 ,
, 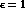 ,
and for neutral pions
,
and for neutral pions 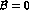 ,
,
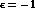 with our definition of Eq. (4).
In terms of the dispersive representation
of Eqs. (6-9), these polarizabilities are simply
related to the
subtraction constants [6] and, of course, the
with our definition of Eq. (4).
In terms of the dispersive representation
of Eqs. (6-9), these polarizabilities are simply
related to the
subtraction constants [6] and, of course, the 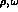 exchange
contributions at s=0 :
exchange
contributions at s=0 :

Moreover, these combinations are sensitively related to the position
of any sub-threshold zeros. In the neighbourhood of s = 0,
the charged and neutral S-wave amplitudes can be
parametrized as
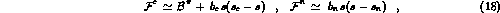
then
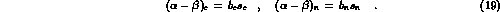
Note that this approximation is only valid for  , since
the amplitudes
have a cusp at
, since
the amplitudes
have a cusp at  threshold, which is particularly marked
in the
threshold, which is particularly marked
in the 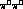 amplitude, see Fig. 25 of Ref. 6 or Fig. 8 of
Bellucci et al. [24]
in 2 loop standard
amplitude, see Fig. 25 of Ref. 6 or Fig. 8 of
Bellucci et al. [24]
in 2 loop standard 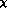 PT or Fig. 6 of Knecht et al. [30] in
1 loop generalized
PT or Fig. 6 of Knecht et al. [30] in
1 loop generalized  PT . Of course
PT . Of course 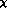 PT has a definite expectation for the values
of
PT has a definite expectation for the values
of 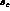 and
and 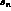 . However,
we have seen from Fig. 7 that present (or even future)
data cannot tell
without a model parametrization whether the sub-threshold
zero in the neutral channel is at
. However,
we have seen from Fig. 7 that present (or even future)
data cannot tell
without a model parametrization whether the sub-threshold
zero in the neutral channel is at
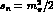 ,
, 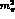 or
or 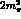 . This variation leads
to a factor
of four difference in the neutral polarizability
. This variation leads
to a factor
of four difference in the neutral polarizability 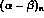 from
from
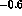 to
to 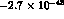 cm
cm .
These values are merely illustrative
.
These values are merely illustrative  ,
in practice the range of uncertainty of a model-independent extraction
is still larger. Moreover, present data even allow
,
in practice the range of uncertainty of a model-independent extraction
is still larger. Moreover, present data even allow 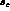 to be zero,
so
to be zero,
so  could
be zero, also with a very large uncertainty.
could
be zero, also with a very large uncertainty.
Rather than use the sub-threshold behaviour around
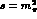 as we have done
in Sect. 3 to fix the S-wave subtraction constants,
as we have done
in Sect. 3 to fix the S-wave subtraction constants, 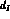 ,
Kaloshin and Serebryakov [31] have attempted a closely related dispersive
analysis in which the subtraction constants for the S-wave
are parametrized directly in terms of the polarizabilities
,
Kaloshin and Serebryakov [31] have attempted a closely related dispersive
analysis in which the subtraction constants for the S-wave
are parametrized directly in terms of the polarizabilities
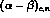 .
They find in units of
.
They find in units of 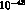 cm
cm :
:
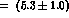 ;
; 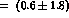 .
As just remarked a value of = 0 is perfectly consistent
with the charged channel data, so why
have Kaloshin and Serebryakov [31] excluded this by many standard
deviations ?
This is because though they only fit the Mark II
.
As just remarked a value of = 0 is perfectly consistent
with the charged channel data, so why
have Kaloshin and Serebryakov [31] excluded this by many standard
deviations ?
This is because though they only fit the Mark II  data [7]
below 400 MeV, they include
in their fit data on
data [7]
below 400 MeV, they include
in their fit data on 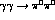 [10] up to 850 MeV and yet assume they
know the form of all the cross-channel exchanges
[10] up to 850 MeV and yet assume they
know the form of all the cross-channel exchanges  ,
,
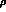 ,
,  very far from their t and u-channel poles.
The existence of the
very far from their t and u-channel poles.
The existence of the 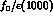 and
and  ,
the former markedly affects data at
800 MeV, because of its large width (Fig. 12), require many more
exchanges than
,
the former markedly affects data at
800 MeV, because of its large width (Fig. 12), require many more
exchanges than  and
and  . Moreover, even in going from the
. Moreover, even in going from the
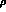 and
and  poles at
poles at 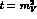 , where the couplings are, of course,
determined by the measured
, where the couplings are, of course,
determined by the measured 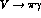 rates, to the Compton threshold
at
rates, to the Compton threshold
at 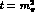 , the couplings can change by a factor of 2 --- a simple
Veneziano-like model with towers of resonances,
not just the
, the couplings can change by a factor of 2 --- a simple
Veneziano-like model with towers of resonances,
not just the 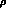 and
and  gives a factor of
gives a factor of 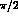
 . To then assume at 850 MeV, where
. To then assume at 850 MeV, where 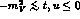 ,
the pure
,
the pure
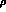 and
and  exchange amplitudes have the same couplings as at
exchange amplitudes have the same couplings as at
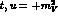 is a grossly over-simplified model leading to far too small
an estimate of the uncertainties
on the supposedly determined polarizabilities. That the details of the
cross-channel exchanges become increasingly
important at higher
is a grossly over-simplified model leading to far too small
an estimate of the uncertainties
on the supposedly determined polarizabilities. That the details of the
cross-channel exchanges become increasingly
important at higher 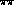 masses can be seen
from Fig. 3 and from the band shown in Fig. 6.
masses can be seen
from Fig. 3 and from the band shown in Fig. 6.
We now turn to the determination of 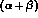 combinations of polarizabilities.
While the
combinations of polarizabilities.
While the 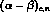 are related to how the
are related to how the 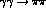 S-waves approach their Born term as
S-waves approach their Born term as 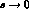 ,
Eq. (16), the
,
Eq. (16), the 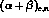 are determined by the way the helicity two
D-waves approach their Born term at the same Compton threshold.
These are even more difficult to determine from
are determined by the way the helicity two
D-waves approach their Born term at the same Compton threshold.
These are even more difficult to determine from 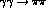 data. As we have
stressed, it is only in the very low energy region that cross-channel
exchange contributions are accurately calculable. Below 500 MeV, the
D-wave amplitude is overwhelmingly (
data. As we have
stressed, it is only in the very low energy region that cross-channel
exchange contributions are accurately calculable. Below 500 MeV, the
D-wave amplitude is overwhelmingly (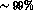 ) controlled by its Born component. It is the residual
) controlled by its Born component. It is the residual 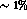 that has
to be extrapolated to s=0 to determine the
that has
to be extrapolated to s=0 to determine the 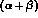 combinations of
polarizabilities,
clearly an impossible
task with present data that only cover a very limited part of the
angular range.
More accurate separation of higher waves with helicity two will become
possible using
the azimuthal information that the DA
combinations of
polarizabilities,
clearly an impossible
task with present data that only cover a very limited part of the
angular range.
More accurate separation of higher waves with helicity two will become
possible using
the azimuthal information that the DA NE
NE  experiment should
provide [32,33,34].
However, this has not deterred Kaloshin, Persikov and
Serebryakov [35]
from attempting
a first estimate of the
experiment should
provide [32,33,34].
However, this has not deterred Kaloshin, Persikov and
Serebryakov [35]
from attempting
a first estimate of the 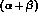 with amazing results.
They have once again, even up to 1.4 GeV in
with amazing results.
They have once again, even up to 1.4 GeV in 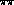 mass, assumed only elementary
mass, assumed only elementary
 ,
,
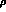 and
and  exchange determine the left hand cut effects. No obvious
t, u-dependence is included in the
pole numerators, even though t, u-channel unitarity demand these.
They then add an
exchange determine the left hand cut effects. No obvious
t, u-dependence is included in the
pole numerators, even though t, u-channel unitarity demand these.
They then add an  direct
channel contribution assuming this to be wholly helicity two with no
S-wave background under this. While
present data are not incompatible with this, they are equally consistent
(see Fig. 12)
with 30% of the I=0 cross-section from 1--1.4 GeV being
S-wave [11,8]
and
possibly 30% of the D-wave
having helicity zero [11]. This provides at least a 40--50%
uncertainty in the
direct
channel contribution assuming this to be wholly helicity two with no
S-wave background under this. While
present data are not incompatible with this, they are equally consistent
(see Fig. 12)
with 30% of the I=0 cross-section from 1--1.4 GeV being
S-wave [11,8]
and
possibly 30% of the D-wave
having helicity zero [11]. This provides at least a 40--50%
uncertainty in the
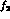 -contribution to the helicity two D-wave cross-section.
Yet Kaloshin et al. [35] quote
values of
-contribution to the helicity two D-wave cross-section.
Yet Kaloshin et al. [35] quote
values of 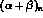 with 5% errors :
with 5% errors : 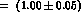 , far away at
s = 0.
, far away at
s = 0.
In the dispersive treatment discussed above, the description of
the 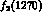 region in terms of Eq. (12),
region in terms of Eq. (12), 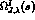 embodies
the expected Breit-Wigner shape
of the resonance, while
embodies
the expected Breit-Wigner shape
of the resonance, while 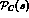 provides a smooth modulation of
this over the peak
in much the same way as the
provides a smooth modulation of
this over the peak
in much the same way as the 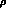 -line shape in
-line shape in 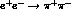 differs smoothly from that in
differs smoothly from that in 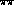 elastic scattering. The exact form of
elastic scattering. The exact form of
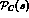 depends, of course, on the structure of the left hand cut discontinuity embodied
in the model for
depends, of course, on the structure of the left hand cut discontinuity embodied
in the model for
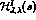 defining
defining 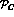 in Eq. (12). Kaloshin et al. take
their analogue of
in Eq. (12). Kaloshin et al. take
their analogue of
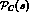 to be a constant, as far as its s-dependence is concerned.
However,
to be a constant, as far as its s-dependence is concerned.
However, 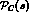 is really built from many t and u-channel
exchanges.
While these do generate a smooth form over the
is really built from many t and u-channel
exchanges.
While these do generate a smooth form over the 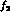 -region from
1 to 1.4 GeV, for almost any couplings, it is
the exact values of these individually that determines the extrapolation
to s = 0 (cf. the analogue of Eq. (17)). Consequently, the
analysis of
Kaloshin, Persikov and Serebryakov [35] is misguided.
Fitting in the
-region from
1 to 1.4 GeV, for almost any couplings, it is
the exact values of these individually that determines the extrapolation
to s = 0 (cf. the analogue of Eq. (17)). Consequently, the
analysis of
Kaloshin, Persikov and Serebryakov [35] is misguided.
Fitting in the 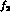 -region can in no way determine the
polarizability
-region can in no way determine the
polarizability 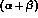 charged or neutral. This is obvious from the
structure of Fig. 3, where exchanges crowd in near the physical region
and only their collective
effect is measured, whereas in extrapolating to s=0, it is the
individual exchange
contributions that matter.
charged or neutral. This is obvious from the
structure of Fig. 3, where exchanges crowd in near the physical region
and only their collective
effect is measured, whereas in extrapolating to s=0, it is the
individual exchange
contributions that matter.
All this means that the only way to measure the pion polarizabilities is in the
Compton scattering process near threshold and not in 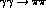 . Though low energy
. Though low energy
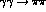 scattering is seemingly close to the
Compton threshold (
scattering is seemingly close to the
Compton threshold (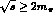 to
to 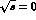 ) and so
the extrapolation not very far, the dominance of the pion pole (for
final state interaction effects, for example)
means that the energy scale for this continuation is
) and so
the extrapolation not very far, the dominance of the pion pole (for
final state interaction effects, for example)
means that the energy scale for this continuation is 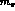 .
Thus the polarizabilities cannot be determined accurately from
.
Thus the polarizabilities cannot be determined accurately from
 experiments in a model-independent way and must
be measured in the Compton scattering region [29].
experiments in a model-independent way and must
be measured in the Compton scattering region [29].



Next: 5 Summary
Up: Chapter 10 Section 1
Previous: 3 Dispersive Predictions
Carlos E.Piedrafita
 , magnetic
, magnetic  --- of a
particle, like its charge
radius, reflect its response to an electromagnetic
stimulus [28,21,29].
They are related
to how the Compton amplitudes approach the Born limit at threshold. Thus
the combination
--- of a
particle, like its charge
radius, reflect its response to an electromagnetic
stimulus [28,21,29].
They are related
to how the Compton amplitudes approach the Born limit at threshold. Thus
the combination
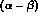 is determined by the slope of the S-wave
is determined by the slope of the S-wave 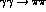 amplitude at the cross-channel threshold :
amplitude at the cross-channel threshold :
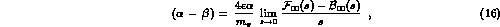
 is the one-pion-exchange
Born amplitude,
is the one-pion-exchange
Born amplitude, 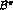 ,
, 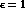 ,
and for neutral pions
,
and for neutral pions 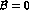 ,
,
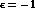 with our definition of Eq. (
with our definition of Eq. (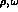 exchange
contributions at s=0 :
exchange
contributions at s=0 :

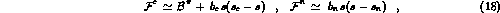
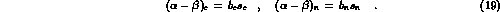
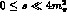 , since
the amplitudes
have a cusp at
, since
the amplitudes
have a cusp at 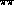 threshold, which is particularly marked
in the
threshold, which is particularly marked
in the 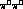 amplitude, see Fig. 25 of Ref. 6 or Fig. 8 of
Bellucci et al. [
amplitude, see Fig. 25 of Ref. 6 or Fig. 8 of
Bellucci et al. [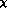 PT or Fig. 6 of Knecht et al. [
PT or Fig. 6 of Knecht et al. [ PT . Of course
PT . Of course 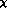 PT has a definite expectation for the values
of
PT has a definite expectation for the values
of 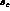 and
and 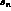 . However,
we have seen from Fig. 7 that present (or even future)
data cannot tell
without a model parametrization whether the sub-threshold
zero in the neutral channel is at
. However,
we have seen from Fig. 7 that present (or even future)
data cannot tell
without a model parametrization whether the sub-threshold
zero in the neutral channel is at
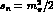 ,
, 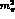 or
or 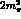 . This variation leads
to a factor
of four difference in the neutral polarizability
. This variation leads
to a factor
of four difference in the neutral polarizability 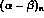 from
from
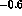 to
to 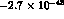 cm
cm .
These values are merely illustrative
.
These values are merely illustrative 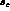 to be zero,
so
to be zero,
so  could
be zero, also with a very large uncertainty.
could
be zero, also with a very large uncertainty.
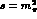 as we have done
in Sect. 3 to fix the S-wave subtraction constants,
as we have done
in Sect. 3 to fix the S-wave subtraction constants, 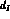 ,
Kaloshin and Serebryakov [
,
Kaloshin and Serebryakov [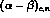 .
They find in units of
.
They find in units of 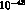 cm
cm :
:
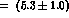 ;
; 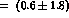 .
As just remarked a value of = 0 is perfectly consistent
with the charged channel data, so why
have Kaloshin and Serebryakov [
.
As just remarked a value of = 0 is perfectly consistent
with the charged channel data, so why
have Kaloshin and Serebryakov [ data [
data [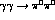 [
[ ,
,
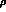 ,
,  very far from their t and u-channel poles.
The existence of the
very far from their t and u-channel poles.
The existence of the 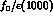 and
and  ,
the former markedly affects data at
800 MeV, because of its large width (Fig. 12), require many more
exchanges than
,
the former markedly affects data at
800 MeV, because of its large width (Fig. 12), require many more
exchanges than  and
and  . Moreover, even in going from the
. Moreover, even in going from the
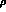 and
and  poles at
poles at 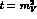 , where the couplings are, of course,
determined by the measured
, where the couplings are, of course,
determined by the measured 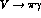 rates, to the Compton threshold
at
rates, to the Compton threshold
at 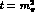 , the couplings can change by a factor of 2 --- a simple
Veneziano-like model with towers of resonances,
not just the
, the couplings can change by a factor of 2 --- a simple
Veneziano-like model with towers of resonances,
not just the 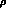 and
and  gives a factor of
gives a factor of 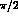
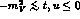 ,
the pure
,
the pure
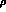 and
and  exchange amplitudes have the same couplings as at
exchange amplitudes have the same couplings as at
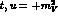 is a grossly over-simplified model leading to far too small
an estimate of the uncertainties
on the supposedly determined polarizabilities. That the details of the
cross-channel exchanges become increasingly
important at higher
is a grossly over-simplified model leading to far too small
an estimate of the uncertainties
on the supposedly determined polarizabilities. That the details of the
cross-channel exchanges become increasingly
important at higher 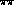 masses can be seen
from Fig. 3 and from the band shown in Fig. 6.
masses can be seen
from Fig. 3 and from the band shown in Fig. 6.
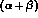 combinations of polarizabilities.
While the
combinations of polarizabilities.
While the 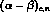 are related to how the
are related to how the 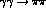 S-waves approach their Born term as
S-waves approach their Born term as 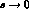 ,
Eq. (
,
Eq. (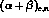 are determined by the way the helicity two
D-waves approach their Born term at the same Compton threshold.
These are even more difficult to determine from
are determined by the way the helicity two
D-waves approach their Born term at the same Compton threshold.
These are even more difficult to determine from 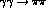 data. As we have
stressed, it is only in the very low energy region that cross-channel
exchange contributions are accurately calculable. Below 500 MeV, the
D-wave amplitude is overwhelmingly (
data. As we have
stressed, it is only in the very low energy region that cross-channel
exchange contributions are accurately calculable. Below 500 MeV, the
D-wave amplitude is overwhelmingly (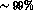 ) controlled by its Born component. It is the residual
) controlled by its Born component. It is the residual 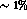 that has
to be extrapolated to s=0 to determine the
that has
to be extrapolated to s=0 to determine the 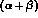 combinations of
polarizabilities,
clearly an impossible
task with present data that only cover a very limited part of the
angular range.
More accurate separation of higher waves with helicity two will become
possible using
the azimuthal information that the DA
combinations of
polarizabilities,
clearly an impossible
task with present data that only cover a very limited part of the
angular range.
More accurate separation of higher waves with helicity two will become
possible using
the azimuthal information that the DA NE
NE  experiment should
provide [
experiment should
provide [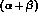 with amazing results.
They have once again, even up to 1.4 GeV in
with amazing results.
They have once again, even up to 1.4 GeV in 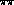 mass, assumed only elementary
mass, assumed only elementary
 ,
,
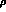 and
and  exchange determine the left hand cut effects. No obvious
t, u-dependence is included in the
pole numerators, even though t, u-channel unitarity demand these.
They then add an
exchange determine the left hand cut effects. No obvious
t, u-dependence is included in the
pole numerators, even though t, u-channel unitarity demand these.
They then add an  direct
channel contribution assuming this to be wholly helicity two with no
S-wave background under this. While
present data are not incompatible with this, they are equally consistent
(see Fig. 12)
with 30% of the I=0 cross-section from 1--1.4 GeV being
S-wave [
direct
channel contribution assuming this to be wholly helicity two with no
S-wave background under this. While
present data are not incompatible with this, they are equally consistent
(see Fig. 12)
with 30% of the I=0 cross-section from 1--1.4 GeV being
S-wave [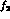 -contribution to the helicity two D-wave cross-section.
Yet Kaloshin et al. [
-contribution to the helicity two D-wave cross-section.
Yet Kaloshin et al. [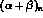 with 5% errors :
with 5% errors : 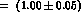 , far away at
s = 0.
, far away at
s = 0.
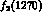 region in terms of Eq. (
region in terms of Eq. (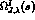 embodies
the expected Breit-Wigner shape
of the resonance, while
embodies
the expected Breit-Wigner shape
of the resonance, while 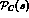 provides a smooth modulation of
this over the peak
in much the same way as the
provides a smooth modulation of
this over the peak
in much the same way as the 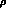 -line shape in
-line shape in 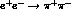 differs smoothly from that in
differs smoothly from that in 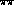 elastic scattering. The exact form of
elastic scattering. The exact form of
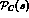 depends, of course, on the structure of the left hand cut discontinuity embodied
in the model for
depends, of course, on the structure of the left hand cut discontinuity embodied
in the model for
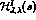 defining
defining 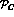 in Eq. (
in Eq. (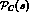 to be a constant, as far as its s-dependence is concerned.
However,
to be a constant, as far as its s-dependence is concerned.
However, 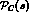 is really built from many t and u-channel
exchanges.
While these do generate a smooth form over the
is really built from many t and u-channel
exchanges.
While these do generate a smooth form over the 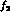 -region from
1 to 1.4 GeV, for almost any couplings, it is
the exact values of these individually that determines the extrapolation
to s = 0 (cf. the analogue of Eq. (
-region from
1 to 1.4 GeV, for almost any couplings, it is
the exact values of these individually that determines the extrapolation
to s = 0 (cf. the analogue of Eq. (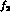 -region can in no way determine the
polarizability
-region can in no way determine the
polarizability 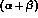 charged or neutral. This is obvious from the
structure of Fig. 3, where exchanges crowd in near the physical region
and only their collective
effect is measured, whereas in extrapolating to s=0, it is the
individual exchange
contributions that matter.
charged or neutral. This is obvious from the
structure of Fig. 3, where exchanges crowd in near the physical region
and only their collective
effect is measured, whereas in extrapolating to s=0, it is the
individual exchange
contributions that matter.
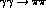 . Though low energy
. Though low energy
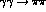 scattering is seemingly close to the
Compton threshold (
scattering is seemingly close to the
Compton threshold (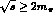 to
to 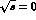 ) and so
the extrapolation not very far, the dominance of the pion pole (for
final state interaction effects, for example)
means that the energy scale for this continuation is
) and so
the extrapolation not very far, the dominance of the pion pole (for
final state interaction effects, for example)
means that the energy scale for this continuation is 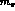 .
Thus the polarizabilities cannot be determined accurately from
.
Thus the polarizabilities cannot be determined accurately from
 experiments in a model-independent way and must
be measured in the Compton scattering region [
experiments in a model-independent way and must
be measured in the Compton scattering region [