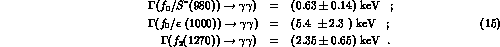Next: 4 Polarizabilities
Up: Chapter 10 Section 1
Previous: 2 The Dispersive Approach
At low energies we can evaluate the dispersion relations
for the S and higher waves, Eqs. (6,10).
We input
- (i)
- the phases of the
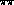 partial wave amplitude from
partial wave amplitude from 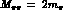 to
800 or 900 MeV
(above that the phases are irrelevant for the
to
800 or 900 MeV
(above that the phases are irrelevant for the 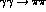 cross-section at
low energies),
cross-section at
low energies),
- (ii)
- the discontinuity of the left hand cut ---
 -exchange plus whatever,
-exchange plus whatever,
- (iii)
- the slope of the
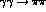 S-wave amplitudes minus their Born
components in the sub-threshold region
needed to fix the subtraction constants,
S-wave amplitudes minus their Born
components in the sub-threshold region
needed to fix the subtraction constants, 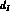 , in
Eq. (6).
, in
Eq. (6).
For orientation, we first perform a model calculation. We input
- (i)
- the phases of
Weinberg's model of
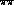 scattering [20],
scattering [20],
- (ii)
- assume only
 -exchange in the crossed channels,
and
-exchange in the crossed channels,
and
- (iii)
- we fix the slopes at
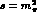 from one loop
from one loop 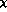 PT
[18,19]
as there the neutral S-wave vanishes, i.e.
PT
[18,19]
as there the neutral S-wave vanishes, i.e. 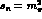 .
.
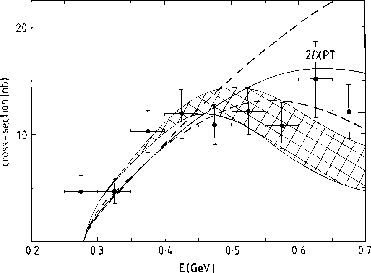
Figure 6: Integrated cross-section for
 as a function of the
as a function of the 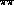 invariant mass,
invariant mass, 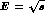 . The data are from Crystal Ball
[3] scaled to the full angular range by a factor of 1.25. The
band depicts our dispersive prediction using the central phases of
Fig. 17 of Ref. 6 with
. The data are from Crystal Ball
[3] scaled to the full angular range by a factor of 1.25. The
band depicts our dispersive prediction using the central phases of
Fig. 17 of Ref. 6 with 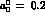 . The shaded area is a
reflection of both the experimental uncertainty above 500 MeV in the
S-wave
. The shaded area is a
reflection of both the experimental uncertainty above 500 MeV in the
S-wave 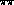 phases and the different asymptotics for the
vector exchanges [6]. The band delineated by the dashed
lines and the solid central curve marked
phases and the different asymptotics for the
vector exchanges [6]. The band delineated by the dashed
lines and the solid central curve marked 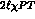 is the
prediction of 2 loop Chiral Perturbation Theory [24].
is the
prediction of 2 loop Chiral Perturbation Theory [24].
We turn the handle of the machinery defined in
Eqs. (3-10,13,14) and out comes the
cross-section for 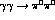 marked
marked 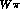 " shown in Fig. 5. Near
threshold this is identical with the one loop calculation of this
process in
" shown in Fig. 5. Near
threshold this is identical with the one loop calculation of this
process in 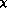 PT by Bijnens and Cornet and by Donoghue, Holstein and
Lin [18,19]. Both the lines
PT by Bijnens and Cornet and by Donoghue, Holstein and
Lin [18,19]. Both the lines  " and
" and
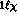 PT" exhibit the much discussed disagreement with the
near threshold data of Crystal Ball [10]. Above 500 MeV, the
dispersive result flattens out, as it has to from unitarity, unlike
one loop
PT" exhibit the much discussed disagreement with the
near threshold data of Crystal Ball [10]. Above 500 MeV, the
dispersive result flattens out, as it has to from unitarity, unlike
one loop 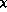 PT . This calculation, which is here wholly numerical, has
also been performed semi-analytically by Donoghue and
Holstein [21], who simplify this exercise by setting
PT . This calculation, which is here wholly numerical, has
also been performed semi-analytically by Donoghue and
Holstein [21], who simplify this exercise by setting
 so that
so that 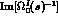 can be replaced by
can be replaced by 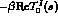 in order to compute the integral in Eq. (6).
in order to compute the integral in Eq. (6).
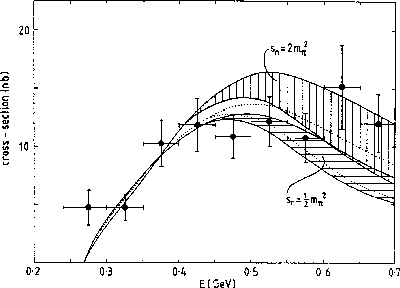
Figure 7: Integrated cross-section for
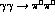 as a function of the
as a function of the 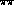 invariant mass,
invariant mass, 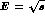 . The data are from Crystal
Ball [10] scaled to the full angular range by a factor of
1.25. The three bands show the effect of varying the sub-threshold
zero for
. The data are from Crystal
Ball [10] scaled to the full angular range by a factor of
1.25. The three bands show the effect of varying the sub-threshold
zero for 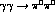 from
from 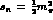 (the lower, horizontally shaded region) to
(the lower, horizontally shaded region) to
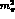 (the unshaded region bounded by the dotted lines) to
(the unshaded region bounded by the dotted lines) to
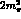 (the higher, vertically shaded region). Again the bands
mark the uncertainties in the calculations [6].
(the higher, vertically shaded region). Again the bands
mark the uncertainties in the calculations [6].
After this consistency check, we next input experimental 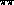 phases, based on analyses of the CERN-Munich results by Ochs, by
Estabrooks and Martin and by Hoogland et al. [22] extrapolated
to threshold using the Roy equations ( which are the partial wave
projection of twice subtracted dispersion relations embodying full
three channel crossing symmetry ) for different values of the I=0
S-wave
phases, based on analyses of the CERN-Munich results by Ochs, by
Estabrooks and Martin and by Hoogland et al. [22] extrapolated
to threshold using the Roy equations ( which are the partial wave
projection of twice subtracted dispersion relations embodying full
three channel crossing symmetry ) for different values of the I=0
S-wave 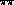 scattering length
scattering length  . The complete details of these
calculations are given in [6]. Figs. 5-7 show the predictions
for the integrated
. The complete details of these
calculations are given in [6]. Figs. 5-7 show the predictions
for the integrated 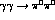 cross-section. Firstly, in Fig. 5 we have the
curve
cross-section. Firstly, in Fig. 5 we have the
curve 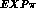 " with the input of
" with the input of  exchange, experimental
exchange, experimental
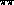 phases with
phases with 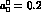 and
and 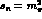 . This is
already in better agreement with the near threshold data. In Fig. 6
we add, to the inputs of Fig. 5,
. This is
already in better agreement with the near threshold data. In Fig. 6
we add, to the inputs of Fig. 5, 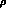 and
and  exchanges. The
values of the couplings of the various t and u-channel exchanges
on-mass shell have been given by Ko [23] and are discussed
in [6]. The addition of
exchanges. The
values of the couplings of the various t and u-channel exchanges
on-mass shell have been given by Ko [23] and are discussed
in [6]. The addition of 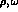 exchange brings an even
better measure of agreement with experiment over a much larger energy
range up to 500-600 MeV (as may have been anticipated from Fig. 3).
In Fig. 6 we also show the band (
exchange brings an even
better measure of agreement with experiment over a much larger energy
range up to 500-600 MeV (as may have been anticipated from Fig. 3).
In Fig. 6 we also show the band (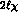 PT) given by the recently
completed two loop calculation in
PT) given by the recently
completed two loop calculation in 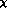 PT by Bellucci, Gasser and
Sainio [24]. This is in good agreement with the dispersive
results --- the small discrepancy near threshold is due to a small
difference in the
PT by Bellucci, Gasser and
Sainio [24]. This is in good agreement with the dispersive
results --- the small discrepancy near threshold is due to a small
difference in the 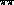 phases input into our calculation and those of
phases input into our calculation and those of
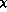 PT near threshold. The two loop calculation depends on a
significant number of new constants, beyond the lowest order
parameters
PT near threshold. The two loop calculation depends on a
significant number of new constants, beyond the lowest order
parameters 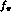 and
and 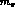 . These new constants have their
analogue in the dispersive approach, Eq. (12), as we comment
on later.
. These new constants have their
analogue in the dispersive approach, Eq. (12), as we comment
on later.
To have an idea of how much the dispersive predictions for 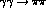 reflect our specific inputs, we illustrate the dependence on the
position,
reflect our specific inputs, we illustrate the dependence on the
position, 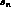 of the zero in the
of the zero in the 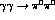 S-wave and on the low energy
S-wave and on the low energy
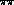 phases. Thus Fig. 7 shows the results with
phases. Thus Fig. 7 shows the results with 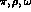 exchanges,
exchanges, 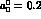 and
and 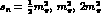 in turn, while Fig. 8 has the same left hand cut, but
with
in turn, while Fig. 8 has the same left hand cut, but
with 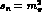 and
and 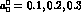 . Of course,
. Of course, 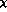 PT
has a definite view of what these parameters
PT
has a definite view of what these parameters  and
and 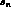 are.
Figs. 6-8 illustrate how data on
are.
Figs. 6-8 illustrate how data on 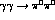 can calibrate these predictions.
can calibrate these predictions.
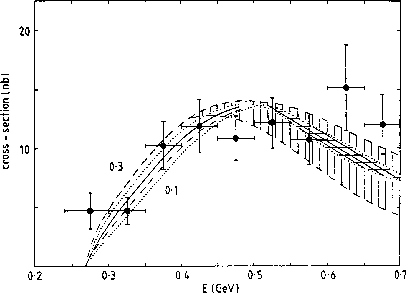
Figure 8: Integrated cross-section for
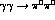 as a function of the
as a function of the 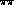 invariant mass,
invariant mass, 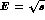 . The data are from Crystal
Ball [10] scaled to the full angular range by a factor of
1.25. The lines, labelled by the value of the I=0
. The data are from Crystal
Ball [10] scaled to the full angular range by a factor of
1.25. The lines, labelled by the value of the I=0 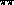 S-wave scattering length in steps of 0.05 from 0.1 to 0.3,
illustrate the effect of different extrapolations of the
S-wave scattering length in steps of 0.05 from 0.1 to 0.3,
illustrate the effect of different extrapolations of the 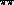 phases
above 520 MeV down to threshold on the dispersive
prediction [6]. The bands above 500 MeV on the
phases
above 520 MeV down to threshold on the dispersive
prediction [6]. The bands above 500 MeV on the
 and 0.3 curves mark the range generated by different
asymptotics for the vector exchanges [6].
and 0.3 curves mark the range generated by different
asymptotics for the vector exchanges [6].
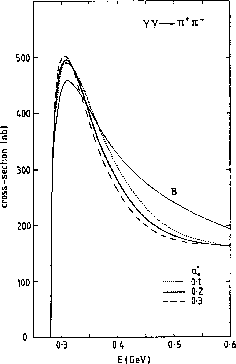
Figure 9: Dispersive predictions for
the integrated cross-section for the
 cross-section as a function of
the
cross-section as a function of
the 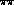 invariant mass,
invariant mass, 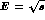 . The lines, labelled
by the value of the I=0
. The lines, labelled
by the value of the I=0 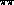 S-wave scattering length in
steps of 0.1 from 0.1 to 0.3, illustrate the effect of different
extrapolations of
S-wave scattering length in
steps of 0.1 from 0.1 to 0.3, illustrate the effect of different
extrapolations of 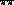 phases above 520 MeV down to
threshold [6] (cf. Fig. 8). The curve marked B is the Born
cross-section [1,3].
phases above 520 MeV down to
threshold [6] (cf. Fig. 8). The curve marked B is the Born
cross-section [1,3].
Fig. 9 shows the corresponding prediction from the present dispersive
approach for 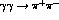 , with the same inputs as for Fig. 8. Notice that in
the charged channel, the effect of final state interactions is to
enhance the Born cross-section very close to threshold and then
suppress it above 360 MeV. One loop
, with the same inputs as for Fig. 8. Notice that in
the charged channel, the effect of final state interactions is to
enhance the Born cross-section very close to threshold and then
suppress it above 360 MeV. One loop 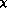 PT for the charged channel
only displays the near threshold enhancement. The two loop
calculation presently under way may be expected to show the same
suppression above 400 MeV, if it is to agree with this dispersive
result and, of course, experiment. This will be an interesting test.
PT for the charged channel
only displays the near threshold enhancement. The two loop
calculation presently under way may be expected to show the same
suppression above 400 MeV, if it is to agree with this dispersive
result and, of course, experiment. This will be an interesting test.
We see from Figs. 8,9 that our dispersive results mean that to
determine the 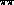 scattering length
scattering length  to an accuracy of
to an accuracy of 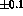 requires the integrated
requires the integrated 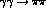 cross-section between 300 and 400
MeV to be measured to an accuracy of
cross-section between 300 and 400
MeV to be measured to an accuracy of 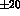 nb in the
nb in the 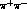 channel
and
channel
and 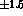 nb in the
nb in the 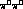 mode. This should be quite possible at
DA
mode. This should be quite possible at
DA NE, but to achieve considerably greater accuracy seems less
likely in the
NE, but to achieve considerably greater accuracy seems less
likely in the  channel. Rather these processes provide a
consistency check on otherwise measured
channel. Rather these processes provide a
consistency check on otherwise measured 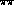 phases and give a way of
pinning down the slopes of the low energy amplitudes that fix the zero
phases and give a way of
pinning down the slopes of the low energy amplitudes that fix the zero
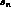 , for example. Of course,
, for example. Of course, 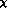 PT makes a definite statement about
how far from
PT makes a definite statement about
how far from 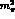 the zero position,
the zero position, 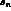 , can be, but tests
of this theory require us to analyse data without inputting this
information. As seen from the predictions of Fig. 7, to do this very
accurately looks a tall order. We will comment on the implications of
this for the model-independent extraction of the pion polarizabilities
in Sect. 4.
, can be, but tests
of this theory require us to analyse data without inputting this
information. As seen from the predictions of Fig. 7, to do this very
accurately looks a tall order. We will comment on the implications of
this for the model-independent extraction of the pion polarizabilities
in Sect. 4.
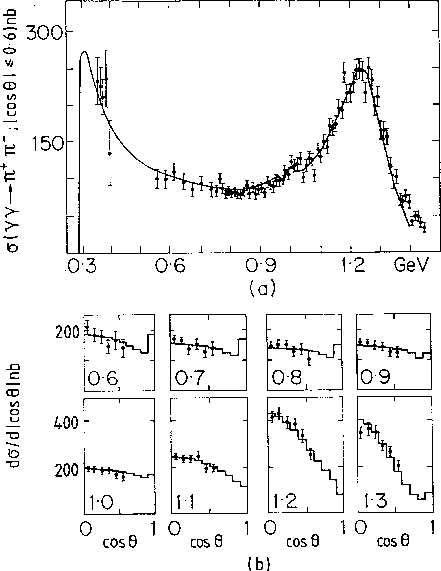
Figure 10:
(a)Integrated cross-section for the
 as a function of the
as a function of the 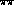 invariant mass,
invariant mass, 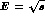 , from Mark II [7] ; (b)
the corresponding differential cross-sections as a function of
, from Mark II [7] ; (b)
the corresponding differential cross-sections as a function of 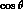 in the stated mass bins (in units of GeV). The curves are
the fits up to 1.4 GeV from the dispersive analysis of Ref. 11.
in the stated mass bins (in units of GeV). The curves are
the fits up to 1.4 GeV from the dispersive analysis of Ref. 11.
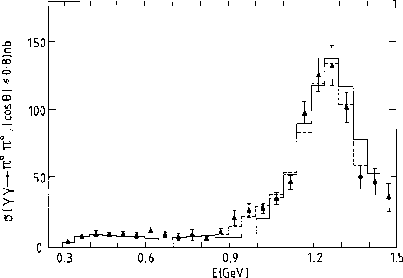
Figure 11: Integrated cross-section for
the 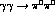 as a function of the
as a function of the
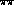 invariant mass,
invariant mass, 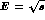 , from Crystal
Ball [10]. The histograms are from the dispersive analysis
up to 1.4 GeV of Ref. 11. They show two fits with different
, from Crystal
Ball [10]. The histograms are from the dispersive analysis
up to 1.4 GeV of Ref. 11. They show two fits with different
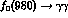 couplings.
couplings.
It is important to realise that the 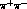 and
and 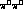 cross-sections are
strongly correlated. A 10% change in the charged data near threshold
would mean a 100% change in the neutral cross-section. Thus early
hints from the very small statistics experiment of DM1/2 [25]
that the low energy
cross-sections are
strongly correlated. A 10% change in the charged data near threshold
would mean a 100% change in the neutral cross-section. Thus early
hints from the very small statistics experiment of DM1/2 [25]
that the low energy 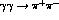 cross-section may be a factor of two larger
than the Born cross-section would have required a
cross-section may be a factor of two larger
than the Born cross-section would have required a 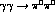 cross-section
of 100 nb [4] rather than the
cross-section
of 100 nb [4] rather than the  10 nb seen by Crystal Ball
(Fig. 4) near threshold. It is this close correlation and agreement
between the Mark II and Crystal Ball data of Figs. 4,10,11 that is so
reassuring. DA
10 nb seen by Crystal Ball
(Fig. 4) near threshold. It is this close correlation and agreement
between the Mark II and Crystal Ball data of Figs. 4,10,11 that is so
reassuring. DA NE should be able to probe this further and allow
a better low energy anchor for partial wave analyses at higher
energies, to which we now turn.
NE should be able to probe this further and allow
a better low energy anchor for partial wave analyses at higher
energies, to which we now turn.
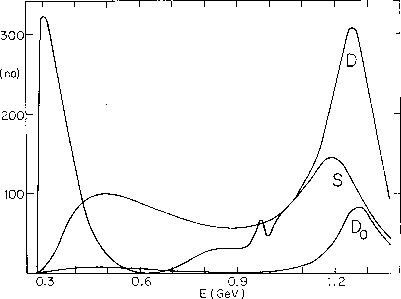
Figure 12: Typical
integrated cross-sections for individual I=0 partial
wave components for 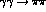 as a function of
as a function of  c.m. energy from the
Amplitude Analysis of the fits of Figs. 10,11 [11].
Notice that the S-wave is highly structured. The peak near threshold
largely reflects the Born term. The dip at 600 MeV is caused by the effect
of final state
interactions on this Born term. These final state interactions are dominated by
the broad
c.m. energy from the
Amplitude Analysis of the fits of Figs. 10,11 [11].
Notice that the S-wave is highly structured. The peak near threshold
largely reflects the Born term. The dip at 600 MeV is caused by the effect
of final state
interactions on this Born term. These final state interactions are dominated by
the broad 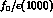 , which is seen up to 1300 MeV,
on top of which is the narrow
, which is seen up to 1300 MeV,
on top of which is the narrow 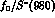 signal. D denotes the
total spin two
component, i.e. the sum
of helicity 0 and 2, while
signal. D denotes the
total spin two
component, i.e. the sum
of helicity 0 and 2, while 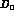 is just the helicity 0 part.
is just the helicity 0 part.
The region of applicability of the dispersive predictions we have
presented here is
below 500 MeV or so. Above that details of cross-channel
exchanges and inelastic phases become increasingly
relevant. The representation of the 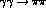 amplitude in terms of left hand cut effects
becomes less and less economical as the various exchanges
amplitude in terms of left hand cut effects
becomes less and less economical as the various exchanges  ,
, 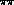 ,
,
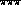 ,
, 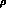 ,
,  ,
, 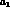 ,
, 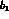 ,
, 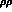 ,
, 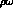 , etc.,
crowd in
towards the
, etc.,
crowd in
towards the 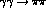 physical region, Fig. 3. Instead a direct channel
representation of the non-pion exchange effects
becomes the most economical, as described above, Eq. (12)
with
physical region, Fig. 3. Instead a direct channel
representation of the non-pion exchange effects
becomes the most economical, as described above, Eq. (12)
with 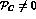 . Of course, the
two descriptions are equivalent, but a single direct channel resonance
is generated by an infinite number of cross-channel exchanges and the
description
of the former is clearly far more economical. Nevertheless, from 600 MeV
to 2 GeV,
the pion exchange Born term continues to play a significant
role (Fig. 3) [3,4].
. Of course, the
two descriptions are equivalent, but a single direct channel resonance
is generated by an infinite number of cross-channel exchanges and the
description
of the former is clearly far more economical. Nevertheless, from 600 MeV
to 2 GeV,
the pion exchange Born term continues to play a significant
role (Fig. 3) [3,4].
This is most
readily illustrated for the D-wave, for which the helicity 2 component
becomes rapidly
important away from threshold.
This partial wave exhibits the 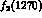 resonance, Figs. 4,10-12, which is
known to be a highly elastic
resonance, Figs. 4,10-12, which is
known to be a highly elastic  resonance with a weak coupling
to the
resonance with a weak coupling
to the 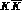 channel [12], just as expected from ideal mixing. It is natural to
assume that this
partial wave in the
channel [12], just as expected from ideal mixing. It is natural to
assume that this
partial wave in the 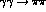 channel continues to have the same
phase as in
channel continues to have the same
phase as in 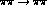 above the inelastic threshold, indeed through the
above the inelastic threshold, indeed through the  region
up to 1.5 GeV, say. Then, the final state corrections to the Born
amplitude are calculable,
using Eqs. (10,12) with
region
up to 1.5 GeV, say. Then, the final state corrections to the Born
amplitude are calculable,
using Eqs. (10,12) with 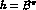 .
As noted by Mennessier [14]
and by Morgan
and the present author [3] in this context and by
Basdevant and Berger [26] in other
related situations, this amplitude actually has a zero close to
the resonance position, here near 1270 MeV. Thus the
modifications to the real pion exchange Born term necessary to make
it agree with unitarity and have the
phase of
.
As noted by Mennessier [14]
and by Morgan
and the present author [3] in this context and by
Basdevant and Berger [26] in other
related situations, this amplitude actually has a zero close to
the resonance position, here near 1270 MeV. Thus the
modifications to the real pion exchange Born term necessary to make
it agree with unitarity and have the
phase of 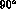 at the
at the 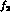 mass, also place a zero there. In terms
of Feynman diagrams, this means the graphs (a, b) of Fig. 13 do not contribute to
the
mass, also place a zero there. In terms
of Feynman diagrams, this means the graphs (a, b) of Fig. 13 do not contribute to
the 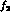 -peak
(though importantly they do affect its observed shape). Rather a direct
-peak
(though importantly they do affect its observed shape). Rather a direct
 coupling
of the
coupling
of the 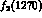 is needed, Fig. 13c, or equivalently
a sum of a large number of cross-channel exchanges. Thus, in accord
with common sense,
the
is needed, Fig. 13c, or equivalently
a sum of a large number of cross-channel exchanges. Thus, in accord
with common sense,
the 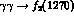 coupling cannot be predicted,
unless one knows all the cross-channel exchange couplings.
Rather one must determine such
resonance couplings from the measured cross-sections.
coupling cannot be predicted,
unless one knows all the cross-channel exchange couplings.
Rather one must determine such
resonance couplings from the measured cross-sections.
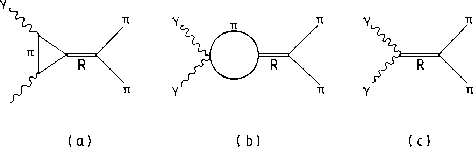
Figure 13:
(a,b) Feynman diagrams displaying the contribution of final
state scattering
for the Born amplitude through a resonance, R, encoded in the
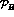 term of Eq. (11) ;
(c) the direct coupling of the same resonance to
term of Eq. (11) ;
(c) the direct coupling of the same resonance to
 and
and 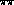 emobodied in the
emobodied in the
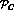 term of Eq. (11).
term of Eq. (11).
An exactly analogous zero (seen in Fig. 12) occurs in the I=0 S-wave
Born amplitude, modified by
final state interactions, at 600 MeV [3], as a result of the broad
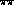 enhancement, the
enhancement, the
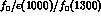 . Again simply adding Breit-Wigners to Born amplitudes fails
to respect Watson's
theorem and the above machinery is essential for any meaningful extraction
of resonance couplings. Thus to go beyond about 500 MeV in describing
. Again simply adding Breit-Wigners to Born amplitudes fails
to respect Watson's
theorem and the above machinery is essential for any meaningful extraction
of resonance couplings. Thus to go beyond about 500 MeV in describing
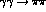 scattering, one must include direct
scattering, one must include direct 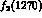 ,
,  and
and 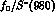 couplings
couplings  in a way consistent with analyticity,
Watson's theorem and Low's low energy theorem. Such an
analysis was performed by David Morgan and myself [11] to the earlier
Crystal Ball statistics on
in a way consistent with analyticity,
Watson's theorem and Low's low energy theorem. Such an
analysis was performed by David Morgan and myself [11] to the earlier
Crystal Ball statistics on 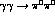 [10]
and Mark II results on
[10]
and Mark II results on 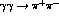 [7] and a new analysis was begun
together with Karch [27],
incorporating the increased Crystal Ball statistics above 800 MeV and
the newer CELLO data [8]
on the charged channel. In Figs. 10,11 are shown illustrative results
(the corresponding plots for
[7] and a new analysis was begun
together with Karch [27],
incorporating the increased Crystal Ball statistics above 800 MeV and
the newer CELLO data [8]
on the charged channel. In Figs. 10,11 are shown illustrative results
(the corresponding plots for 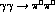 angular distributions
are to be seen in Ref. 11).
One sees that the dispersive
description fits the integrated and differential
cross-sections up to 1400 MeV
remarkably well. This allows a partial wave separation, the I=0 components
being shown in Fig. 12. This leads to the following
couplings [11] for the
angular distributions
are to be seen in Ref. 11).
One sees that the dispersive
description fits the integrated and differential
cross-sections up to 1400 MeV
remarkably well. This allows a partial wave separation, the I=0 components
being shown in Fig. 12. This leads to the following
couplings [11] for the 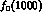 ,
, 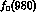 and
and 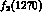 (quoted in the PDG tables [12]) :
(quoted in the PDG tables [12]) :
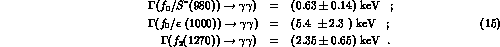



Next: 4 Polarizabilities
Up: Chapter 10 Section 1
Previous: 2 The Dispersive Approach
Carlos E.Piedrafita
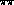 partial wave amplitude from
partial wave amplitude from 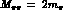 to
800 or 900 MeV
(above that the phases are irrelevant for the
to
800 or 900 MeV
(above that the phases are irrelevant for the 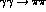 cross-section at
low energies),
cross-section at
low energies),
 -exchange plus whatever,
-exchange plus whatever,
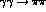 S-wave amplitudes minus their Born
components in the sub-threshold region
needed to fix the subtraction constants,
S-wave amplitudes minus their Born
components in the sub-threshold region
needed to fix the subtraction constants, 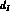 , in
Eq. (6).
, in
Eq. (6).
 scattering [20],
scattering [20],
 -exchange in the crossed channels,
and
-exchange in the crossed channels,
and
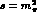 from one loop
from one loop  PT
[18,19]
as there the neutral S-wave vanishes, i.e.
PT
[18,19]
as there the neutral S-wave vanishes, i.e. 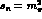 .
.

 as a function of the
as a function of the  invariant mass,
invariant mass, 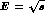 . The data are from Crystal Ball
[
. The data are from Crystal Ball
[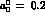 . The shaded area is a
reflection of both the experimental uncertainty above 500 MeV in the
S-wave
. The shaded area is a
reflection of both the experimental uncertainty above 500 MeV in the
S-wave 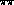 phases and the different asymptotics for the
vector exchanges [
phases and the different asymptotics for the
vector exchanges [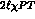 is the
prediction of 2 loop Chiral Perturbation Theory [
is the
prediction of 2 loop Chiral Perturbation Theory [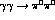 marked
marked 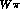 " shown in Fig. 5. Near
threshold this is identical with the one loop calculation of this
process in
" shown in Fig. 5. Near
threshold this is identical with the one loop calculation of this
process in 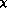 PT by Bijnens and Cornet and by Donoghue, Holstein and
Lin [
PT by Bijnens and Cornet and by Donoghue, Holstein and
Lin [ " and
" and
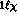 PT" exhibit the much discussed disagreement with the
near threshold data of Crystal Ball [
PT" exhibit the much discussed disagreement with the
near threshold data of Crystal Ball [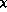 PT . This calculation, which is here wholly numerical, has
also been performed semi-analytically by Donoghue and
Holstein [
PT . This calculation, which is here wholly numerical, has
also been performed semi-analytically by Donoghue and
Holstein [ so that
so that 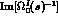 can be replaced by
can be replaced by 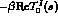 in order to compute the integral in Eq. (
in order to compute the integral in Eq. (
 as a function of the
as a function of the  invariant mass,
invariant mass, 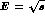 . The data are from Crystal
Ball [
. The data are from Crystal
Ball [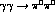 from
from 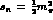 (the lower, horizontally shaded region) to
(the lower, horizontally shaded region) to
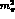 (the unshaded region bounded by the dotted lines) to
(the unshaded region bounded by the dotted lines) to
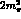 (the higher, vertically shaded region). Again the bands
mark the uncertainties in the calculations [
(the higher, vertically shaded region). Again the bands
mark the uncertainties in the calculations [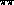 phases, based on analyses of the CERN-Munich results by Ochs, by
Estabrooks and Martin and by Hoogland et al. [
phases, based on analyses of the CERN-Munich results by Ochs, by
Estabrooks and Martin and by Hoogland et al. [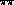 scattering length
scattering length  . The complete details of these
calculations are given in [
. The complete details of these
calculations are given in [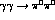 cross-section. Firstly, in Fig. 5 we have the
curve
cross-section. Firstly, in Fig. 5 we have the
curve 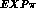 " with the input of
" with the input of  exchange, experimental
exchange, experimental
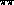 phases with
phases with 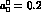 and
and 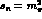 . This is
already in better agreement with the near threshold data. In Fig. 6
we add, to the inputs of Fig. 5,
. This is
already in better agreement with the near threshold data. In Fig. 6
we add, to the inputs of Fig. 5, 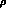 and
and  exchanges. The
values of the couplings of the various t and u-channel exchanges
on-mass shell have been given by Ko [
exchanges. The
values of the couplings of the various t and u-channel exchanges
on-mass shell have been given by Ko [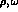 exchange brings an even
better measure of agreement with experiment over a much larger energy
range up to 500-600 MeV (as may have been anticipated from Fig. 3).
In Fig. 6 we also show the band (
exchange brings an even
better measure of agreement with experiment over a much larger energy
range up to 500-600 MeV (as may have been anticipated from Fig. 3).
In Fig. 6 we also show the band (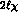 PT) given by the recently
completed two loop calculation in
PT) given by the recently
completed two loop calculation in 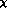 PT by Bellucci, Gasser and
Sainio [
PT by Bellucci, Gasser and
Sainio [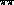 phases input into our calculation and those of
phases input into our calculation and those of
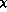 PT near threshold. The two loop calculation depends on a
significant number of new constants, beyond the lowest order
parameters
PT near threshold. The two loop calculation depends on a
significant number of new constants, beyond the lowest order
parameters 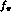 and
and 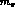 . These new constants have their
analogue in the dispersive approach, Eq. (
. These new constants have their
analogue in the dispersive approach, Eq. (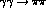 reflect our specific inputs, we illustrate the dependence on the
position,
reflect our specific inputs, we illustrate the dependence on the
position, 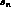 of the zero in the
of the zero in the 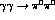 S-wave and on the low energy
S-wave and on the low energy
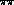 phases. Thus Fig. 7 shows the results with
phases. Thus Fig. 7 shows the results with 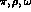 exchanges,
exchanges, 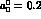 and
and 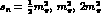 in turn, while Fig. 8 has the same left hand cut, but
with
in turn, while Fig. 8 has the same left hand cut, but
with 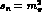 and
and 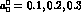 . Of course,
. Of course, 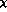 PT
has a definite view of what these parameters
PT
has a definite view of what these parameters  and
and 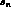 are.
Figs. 6-8 illustrate how data on
are.
Figs. 6-8 illustrate how data on 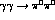 can calibrate these predictions.
can calibrate these predictions.

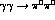 as a function of the
as a function of the 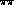 invariant mass,
invariant mass, 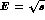 . The data are from Crystal
Ball [
. The data are from Crystal
Ball [ S-wave scattering length in steps of 0.05 from 0.1 to 0.3,
illustrate the effect of different extrapolations of the
S-wave scattering length in steps of 0.05 from 0.1 to 0.3,
illustrate the effect of different extrapolations of the 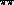 phases
above 520 MeV down to threshold on the dispersive
prediction [
phases
above 520 MeV down to threshold on the dispersive
prediction [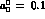 and 0.3 curves mark the range generated by different
asymptotics for the vector exchanges [
and 0.3 curves mark the range generated by different
asymptotics for the vector exchanges [
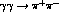 cross-section as a function of
the
cross-section as a function of
the 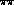 invariant mass,
invariant mass, 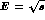 . The lines, labelled
by the value of the I=0
. The lines, labelled
by the value of the I=0 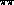 S-wave scattering length in
steps of 0.1 from 0.1 to 0.3, illustrate the effect of different
extrapolations of
S-wave scattering length in
steps of 0.1 from 0.1 to 0.3, illustrate the effect of different
extrapolations of 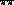 phases above 520 MeV down to
threshold [
phases above 520 MeV down to
threshold [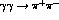 , with the same inputs as for Fig. 8. Notice that in
the charged channel, the effect of final state interactions is to
enhance the Born cross-section very close to threshold and then
suppress it above 360 MeV. One loop
, with the same inputs as for Fig. 8. Notice that in
the charged channel, the effect of final state interactions is to
enhance the Born cross-section very close to threshold and then
suppress it above 360 MeV. One loop 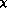 PT for the charged channel
only displays the near threshold enhancement. The two loop
calculation presently under way may be expected to show the same
suppression above 400 MeV, if it is to agree with this dispersive
result and, of course, experiment. This will be an interesting test.
PT for the charged channel
only displays the near threshold enhancement. The two loop
calculation presently under way may be expected to show the same
suppression above 400 MeV, if it is to agree with this dispersive
result and, of course, experiment. This will be an interesting test.
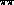 scattering length
scattering length  to an accuracy of
to an accuracy of 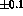 requires the integrated
requires the integrated 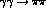 cross-section between 300 and 400
MeV to be measured to an accuracy of
cross-section between 300 and 400
MeV to be measured to an accuracy of 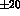 nb in the
nb in the 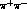 channel
and
channel
and 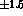 nb in the
nb in the 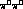 mode. This should be quite possible at
DA
mode. This should be quite possible at
DA NE, but to achieve considerably greater accuracy seems less
likely in the
NE, but to achieve considerably greater accuracy seems less
likely in the  channel. Rather these processes provide a
consistency check on otherwise measured
channel. Rather these processes provide a
consistency check on otherwise measured 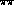 phases and give a way of
pinning down the slopes of the low energy amplitudes that fix the zero
phases and give a way of
pinning down the slopes of the low energy amplitudes that fix the zero
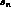 , for example. Of course,
, for example. Of course, 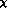 PT makes a definite statement about
how far from
PT makes a definite statement about
how far from 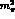 the zero position,
the zero position, 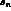 , can be, but tests
of this theory require us to analyse data without inputting this
information. As seen from the predictions of Fig. 7, to do this very
accurately looks a tall order. We will comment on the implications of
this for the model-independent extraction of the pion polarizabilities
in Sect. 4.
, can be, but tests
of this theory require us to analyse data without inputting this
information. As seen from the predictions of Fig. 7, to do this very
accurately looks a tall order. We will comment on the implications of
this for the model-independent extraction of the pion polarizabilities
in Sect. 4.

 as a function of the
as a function of the 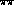 invariant mass,
invariant mass, 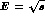 , from Mark II [
, from Mark II [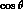 in the stated mass bins (in units of GeV). The curves are
the fits up to 1.4 GeV from the dispersive analysis of Ref. 11.
in the stated mass bins (in units of GeV). The curves are
the fits up to 1.4 GeV from the dispersive analysis of Ref. 11.
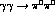 as a function of the
as a function of the
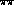 invariant mass,
invariant mass, 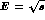 , from Crystal
Ball [
, from Crystal
Ball [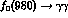 couplings.
couplings.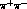 and
and 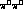 cross-sections are
strongly correlated. A 10% change in the charged data near threshold
would mean a 100% change in the neutral cross-section. Thus early
hints from the very small statistics experiment of DM1/2 [
cross-sections are
strongly correlated. A 10% change in the charged data near threshold
would mean a 100% change in the neutral cross-section. Thus early
hints from the very small statistics experiment of DM1/2 [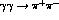 cross-section may be a factor of two larger
than the Born cross-section would have required a
cross-section may be a factor of two larger
than the Born cross-section would have required a 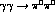 cross-section
of 100 nb [
cross-section
of 100 nb [ 10 nb seen by Crystal Ball
(Fig. 4) near threshold. It is this close correlation and agreement
between the Mark II and Crystal Ball data of Figs. 4,10,11 that is so
reassuring. DA
10 nb seen by Crystal Ball
(Fig. 4) near threshold. It is this close correlation and agreement
between the Mark II and Crystal Ball data of Figs. 4,10,11 that is so
reassuring. DA NE should be able to probe this further and allow
a better low energy anchor for partial wave analyses at higher
energies, to which we now turn.
NE should be able to probe this further and allow
a better low energy anchor for partial wave analyses at higher
energies, to which we now turn.

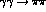 as a function of
as a function of  c.m. energy from the
Amplitude Analysis of the fits of Figs. 10,11 [
c.m. energy from the
Amplitude Analysis of the fits of Figs. 10,11 [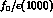 , which is seen up to 1300 MeV,
on top of which is the narrow
, which is seen up to 1300 MeV,
on top of which is the narrow 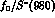 signal. D denotes the
total spin two
component, i.e. the sum
of helicity 0 and 2, while
signal. D denotes the
total spin two
component, i.e. the sum
of helicity 0 and 2, while 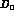 is just the helicity 0 part.
is just the helicity 0 part.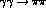 amplitude in terms of left hand cut effects
becomes less and less economical as the various exchanges
amplitude in terms of left hand cut effects
becomes less and less economical as the various exchanges  ,
, 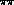 ,
,
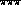 ,
, 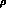 ,
,  ,
, 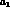 ,
, 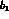 ,
, 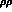 ,
, 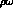 , etc.,
crowd in
towards the
, etc.,
crowd in
towards the 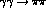 physical region, Fig. 3. Instead a direct channel
representation of the non-pion exchange effects
becomes the most economical, as described above, Eq. (
physical region, Fig. 3. Instead a direct channel
representation of the non-pion exchange effects
becomes the most economical, as described above, Eq. (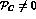 . Of course, the
two descriptions are equivalent, but a single direct channel resonance
is generated by an infinite number of cross-channel exchanges and the
description
of the former is clearly far more economical. Nevertheless, from 600 MeV
to 2 GeV,
the pion exchange Born term continues to play a significant
role (Fig. 3) [
. Of course, the
two descriptions are equivalent, but a single direct channel resonance
is generated by an infinite number of cross-channel exchanges and the
description
of the former is clearly far more economical. Nevertheless, from 600 MeV
to 2 GeV,
the pion exchange Born term continues to play a significant
role (Fig. 3) [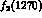 resonance, Figs. 4,10-12, which is
known to be a highly elastic
resonance, Figs. 4,10-12, which is
known to be a highly elastic  resonance with a weak coupling
to the
resonance with a weak coupling
to the 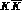 channel [
channel [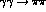 channel continues to have the same
phase as in
channel continues to have the same
phase as in 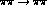 above the inelastic threshold, indeed through the
above the inelastic threshold, indeed through the  region
up to 1.5 GeV, say. Then, the final state corrections to the Born
amplitude are calculable,
using Eqs. (
region
up to 1.5 GeV, say. Then, the final state corrections to the Born
amplitude are calculable,
using Eqs. (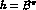 .
As noted by Mennessier [
.
As noted by Mennessier [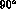 at the
at the 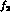 mass, also place a zero there. In terms
of Feynman diagrams, this means the graphs (a, b) of Fig. 13 do not contribute to
the
mass, also place a zero there. In terms
of Feynman diagrams, this means the graphs (a, b) of Fig. 13 do not contribute to
the 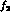 -peak
(though importantly they do affect its observed shape). Rather a direct
-peak
(though importantly they do affect its observed shape). Rather a direct
 coupling
of the
coupling
of the 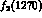 is needed, Fig. 13c, or equivalently
a sum of a large number of cross-channel exchanges. Thus, in accord
with common sense,
the
is needed, Fig. 13c, or equivalently
a sum of a large number of cross-channel exchanges. Thus, in accord
with common sense,
the 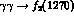 coupling cannot be predicted,
unless one knows all the cross-channel exchange couplings.
Rather one must determine such
resonance couplings from the measured cross-sections.
coupling cannot be predicted,
unless one knows all the cross-channel exchange couplings.
Rather one must determine such
resonance couplings from the measured cross-sections.

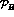 term of Eq. (
term of Eq. ( and
and 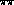 emobodied in the
emobodied in the
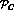 term of Eq. (
term of Eq. (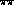 enhancement, the
enhancement, the
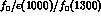 . Again simply adding Breit-Wigners to Born amplitudes fails
to respect Watson's
theorem and the above machinery is essential for any meaningful extraction
of resonance couplings. Thus to go beyond about 500 MeV in describing
. Again simply adding Breit-Wigners to Born amplitudes fails
to respect Watson's
theorem and the above machinery is essential for any meaningful extraction
of resonance couplings. Thus to go beyond about 500 MeV in describing
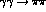 scattering, one must include direct
scattering, one must include direct 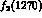 ,
,  and
and 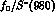 couplings
couplings 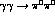 [
[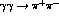 [
[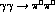 angular distributions
are to be seen in Ref. 11).
One sees that the dispersive
description fits the integrated and differential
cross-sections up to 1400 MeV
remarkably well. This allows a partial wave separation, the I=0 components
being shown in Fig. 12. This leads to the following
couplings [
angular distributions
are to be seen in Ref. 11).
One sees that the dispersive
description fits the integrated and differential
cross-sections up to 1400 MeV
remarkably well. This allows a partial wave separation, the I=0 components
being shown in Fig. 12. This leads to the following
couplings [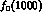 ,
, 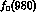 and
and 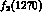 (quoted in the PDG tables [
(quoted in the PDG tables [