


Next: 3 Dispersive Predictions
Up: Chapter 10 Section 1
Previous: 1 Introduction
Let us discuss the properties of the partial wave amplitudes,  , and what
we need
to know to calculate them [13,14,3,4]. Firstly, these amplitudes are
analytic functions of
s. They have a left hand cut starting at s=0 from the pion exchange Born term and
then other cuts running to the left from
, and what
we need
to know to calculate them [13,14,3,4]. Firstly, these amplitudes are
analytic functions of
s. They have a left hand cut starting at s=0 from the pion exchange Born term and
then other cuts running to the left from 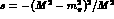 generated
by
generated
by 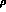 ,
,  and other exchanges of mass M. Of course, only the
nearby part of the left hand cut from s=0 to
and other exchanges of mass M. Of course, only the
nearby part of the left hand cut from s=0 to 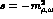 is really known
from one pion exchange [3]. For
is really known
from one pion exchange [3]. For 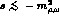 ,
form-factor damping in the
,
form-factor damping in the
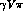 vertex (where
vertex (where 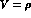 or
or  )
as well as other exchanges affect the left hand cut
discontinuity.
)
as well as other exchanges affect the left hand cut
discontinuity.
The partial wave amplitudes also have a right hand cut generated by
final state interactions. At low energy, the only possible strong interaction
is 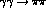 . Then the final state pions will scatter strongly back to
. Then the final state pions will scatter strongly back to 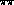 .
Indeed, it
is in this way that the cross-section for
.
Indeed, it
is in this way that the cross-section for 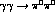 can readily become non-zero :
can readily become non-zero :
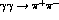
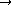
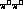 , where the first process in the chain can occur by the
Born term.
Fortunately, such effects are exactly calculable, thanks to two body unitarity.
Above inelastic threshold, which effectively means above
, where the first process in the chain can occur by the
Born term.
Fortunately, such effects are exactly calculable, thanks to two body unitarity.
Above inelastic threshold, which effectively means above 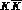 threshold near 1
GeV,
threshold near 1
GeV,  can also go to
can also go to 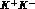 , which in turn can scatter back to
, which in turn can scatter back to 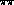 . Though
unitarity still constrains these contributions, one needs information on
. Though
unitarity still constrains these contributions, one needs information on
 and
and 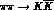 scattering, as well as
scattering, as well as 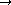
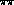 , to know how. This means
it is more
difficult to implement the constraints of unitarity when many channels enter.
However below roughly 1 GeV, elastic unitarity enforces
Watson's theorem [15] that makes the
phase of the partial waves for
, to know how. This means
it is more
difficult to implement the constraints of unitarity when many channels enter.
However below roughly 1 GeV, elastic unitarity enforces
Watson's theorem [15] that makes the
phase of the partial waves for 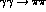 for each I and J,
for each I and J, 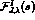 , equal to the
phase of
the corresponding
, equal to the
phase of
the corresponding 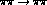 amplitude,
amplitude, 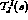 . This is exceedingly useful,
since knowledge
of the phase of an amplitude largely determines the behaviour of its modulus
--- amplitudes being analytic functions. A simple example of this is the phase
rising rapidly from
. This is exceedingly useful,
since knowledge
of the phase of an amplitude largely determines the behaviour of its modulus
--- amplitudes being analytic functions. A simple example of this is the phase
rising rapidly from
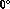 to
to 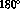 . The modulus then has to peak at a position and width
wholly correlated with the phase variation. This relationship is exemplified
by the
well-known Breit-Wigner formula. The general relation between the phase and
the modulus of the amplitude is embodied in the Omnès representation [16]. Thus
knowing the phase of a partial wave amplitude,
. The modulus then has to peak at a position and width
wholly correlated with the phase variation. This relationship is exemplified
by the
well-known Breit-Wigner formula. The general relation between the phase and
the modulus of the amplitude is embodied in the Omnès representation [16]. Thus
knowing the phase of a partial wave amplitude, 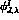 , from
, from
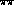 threshold to infinity, we can define a function
threshold to infinity, we can define a function
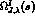 (the Omnès function)
(the Omnès function)
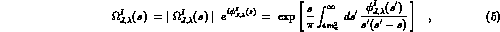
where in the region of elastic unitarity 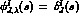 , the
, the 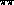 phase shift, independent of the two photon helicity
phase shift, independent of the two photon helicity
 .
This function,
.
This function,  , has the phase
, has the phase  by construction.
The way convergent dispersion relations work,
by construction.
The way convergent dispersion relations work,  at low energies
fortunately does not require detailed knowledge of the phase
at low energies
fortunately does not require detailed knowledge of the phase  above 1 GeV.
We will return to this later.
above 1 GeV.
We will return to this later.
How this information can be used to compute  scattering is explained
in detail
in Ref. 6. Here we sketch the methodology.
We can write an appropriately subtracted dispersion relation for each
partial wave amplitude, specified by I, J and
scattering is explained
in detail
in Ref. 6. Here we sketch the methodology.
We can write an appropriately subtracted dispersion relation for each
partial wave amplitude, specified by I, J and  . For the S-waves
(J=0,
. For the S-waves
(J=0, 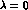 ), these are twice subtracted [17] : two subtractions
to suppress
the dependence at low energies on what the distant left and right hand cut
discontinuites are. That is, there should be only a weak
dependence on both higher mass cross-channel exchanges and the
phases of the
), these are twice subtracted [17] : two subtractions
to suppress
the dependence at low energies on what the distant left and right hand cut
discontinuites are. That is, there should be only a weak
dependence on both higher mass cross-channel exchanges and the
phases of the 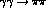 amplitudes above 1 GeV. The lack of knowledge of these
terms is parametrized by two subtraction constants that are fixed by two
crucial low energy constraints. Firstly, Low's theorem that states each partial wave amplitude
equals its corresponding Born term at s=0 --- that follows from QED gauge
invariance. Secondly, from chiral dynamics we have a prediction
in the low energy region for the
amplitude minus its Born term. Thus, for instance the neutral channel
S-wave has a zero at
amplitudes above 1 GeV. The lack of knowledge of these
terms is parametrized by two subtraction constants that are fixed by two
crucial low energy constraints. Firstly, Low's theorem that states each partial wave amplitude
equals its corresponding Born term at s=0 --- that follows from QED gauge
invariance. Secondly, from chiral dynamics we have a prediction
in the low energy region for the
amplitude minus its Born term. Thus, for instance the neutral channel
S-wave has a zero at 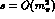 ---
in one loop
Chiral Perturbation Theory (
---
in one loop
Chiral Perturbation Theory (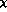 PT ) [18,19] this is at
PT ) [18,19] this is at 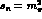 .
In general,
all we know is that these near threshold corrections
are
.
In general,
all we know is that these near threshold corrections
are 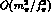 . These low energy limits fix the two
subtraction constants,
. These low energy limits fix the two
subtraction constants, 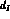 , in the I=0 and 2
, in the I=0 and 2  S-wave amplitudes. Thus
S-wave amplitudes. Thus

The functions 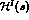 have the complete left hand cut
and no right hand cut. They are given by
have the complete left hand cut
and no right hand cut. They are given by
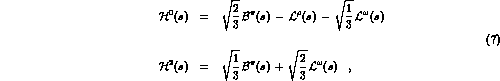
where 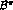 is the one pion exchange Born term and
is the one pion exchange Born term and
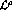 ,
,
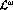 denote the contributions
to the left-hand cut generated by exchanges with
denote the contributions
to the left-hand cut generated by exchanges with 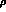 and
and  quantum numbers, respectively.
Then the combinations in the charged and neutral channels are :
quantum numbers, respectively.
Then the combinations in the charged and neutral channels are :
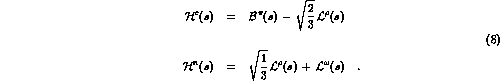
According to Low's theorem :
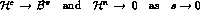 ,
so in turn this means :
,
so in turn this means :
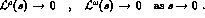 Recalling
Recalling 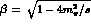 (Eq. (1)), the S-wave
Born amplitude
is, for example, [1,3]
(Eq. (1)), the S-wave
Born amplitude
is, for example, [1,3]
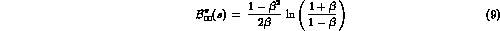
with a cut for 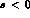 .
.
The fixing of subtraction constants by appeal to chiral dynamics
only affects the S-wave amplitudes.
The higher partial waves satisfy
essentially once subtracted dispersion relations on dividing out their known
threshold behaviour, so that only Low's QED theorem is needed for these waves.
Thus [3]

where the 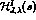 are the appropriate partial waves of the left hand cut
components of Eq. (8).
Using Eqs. (3, 5-10), the cross-sections can
then be deduced from these partial
wave amplitudes.
are the appropriate partial waves of the left hand cut
components of Eq. (8).
Using Eqs. (3, 5-10), the cross-sections can
then be deduced from these partial
wave amplitudes.
It is useful for our later discussion, though not necessary for our low energy
calculations, to note that
these partial wave amplitudes , for all J, can be expressed quite generally [3] as :
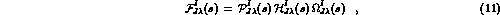
where the function 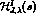 has the left hand cut, Eq. (8),
and
has the left hand cut, Eq. (8),
and 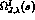 the right hand cut, Eq. (5), and
the right hand cut, Eq. (5), and 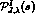 is a
real polynomial. While
is a
real polynomial. While 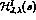 is the full left hand cut function, it is often
convenient to model this function by some
is the full left hand cut function, it is often
convenient to model this function by some 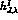 (for instance, the
Born term) and rewrite Eq. (11) as
(for instance, the
Born term) and rewrite Eq. (11) as
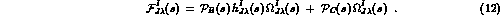
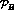 and
and 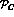 (with
(with 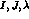 labels suppressed)
may now be more complicated functions along the
left hand cut, but they will continue to be smooth along the right hand cut away from their
singularities. In physical terms, the first term models the simple well
understood cross-channel exchanges and then
labels suppressed)
may now be more complicated functions along the
left hand cut, but they will continue to be smooth along the right hand cut away from their
singularities. In physical terms, the first term models the simple well
understood cross-channel exchanges and then 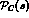 incorporates the
rest as direct channel contributions. Near
incorporates the
rest as direct channel contributions. Near 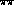 threshold,
threshold,
 is just the pion exchange Born term and there are
essentially no direct channel effects other than those of final state
interactions automatically included in Eqs. (11,12). There
is just the pion exchange Born term and there are
essentially no direct channel effects other than those of final state
interactions automatically included in Eqs. (11,12). There
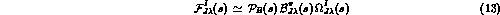
to a good approximation. It is this fact that allows the low energy
cross-section to be accurately predicted as we discuss in the next section.
One can go to slightly higher  masses, 500 MeV or so, by taking
masses, 500 MeV or so, by taking
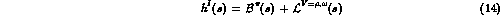
in Eq. (12) with  still zero. However, above
that energy, direct channel effects ( or equivalently heavier mass
cross-channel exchanges ) become increasingly important and definite
predictions possible near threshold must give way to fitting
data [3,4,11].
This is necessary to determine the form of
still zero. However, above
that energy, direct channel effects ( or equivalently heavier mass
cross-channel exchanges ) become increasingly important and definite
predictions possible near threshold must give way to fitting
data [3,4,11].
This is necessary to determine the form of  and
hence the direct channel couplings.
and
hence the direct channel couplings.
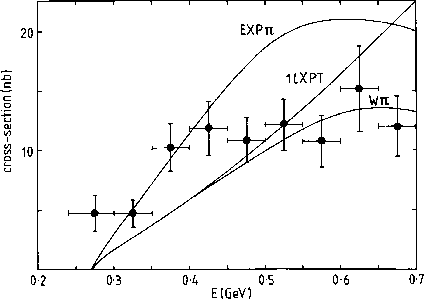
Figure 5: Integrated cross-section for
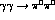 as a function of the
as a function of the 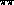 invariant mass,
invariant mass, 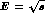 . The data are
from Crystal Ball [3]
scaled to the full angular range by a factor of 1.25.
The line marked
. The data are
from Crystal Ball [3]
scaled to the full angular range by a factor of 1.25.
The line marked 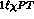 is the prediction of one loop Chiral Perturbation Theory [18,19].
The curve marked
is the prediction of one loop Chiral Perturbation Theory [18,19].
The curve marked 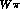 " is the dispersive calculation
using Weinberg phases [20],
while that
labelled
" is the dispersive calculation
using Weinberg phases [20],
while that
labelled 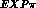 " are the predictions
from experimental
" are the predictions
from experimental 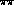 phases
as described in [6] --- both with just
phases
as described in [6] --- both with just  -exchange
for the left hand cut.
-exchange
for the left hand cut.



Next: 3 Dispersive Predictions
Up: Chapter 10 Section 1
Previous: 1 Introduction
Carlos E.Piedrafita
 , and what
we need
to know to calculate them [13,14,3,4]. Firstly, these amplitudes are
analytic functions of
s. They have a left hand cut starting at s=0 from the pion exchange Born term and
then other cuts running to the left from
, and what
we need
to know to calculate them [13,14,3,4]. Firstly, these amplitudes are
analytic functions of
s. They have a left hand cut starting at s=0 from the pion exchange Born term and
then other cuts running to the left from 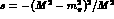 generated
by
generated
by 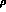 ,
,  and other exchanges of mass M. Of course, only the
nearby part of the left hand cut from s=0 to
and other exchanges of mass M. Of course, only the
nearby part of the left hand cut from s=0 to 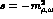 is really known
from one pion exchange [3]. For
is really known
from one pion exchange [3]. For 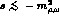 ,
form-factor damping in the
,
form-factor damping in the
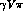 vertex (where
vertex (where 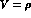 or
or  )
as well as other exchanges affect the left hand cut
discontinuity.
)
as well as other exchanges affect the left hand cut
discontinuity.
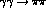 . Then the final state pions will scatter strongly back to
. Then the final state pions will scatter strongly back to 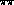 .
Indeed, it
is in this way that the cross-section for
.
Indeed, it
is in this way that the cross-section for 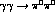 can readily become non-zero :
can readily become non-zero :
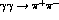
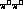 , where the first process in the chain can occur by the
Born term.
Fortunately, such effects are exactly calculable, thanks to two body unitarity.
Above inelastic threshold, which effectively means above
, where the first process in the chain can occur by the
Born term.
Fortunately, such effects are exactly calculable, thanks to two body unitarity.
Above inelastic threshold, which effectively means above 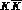 threshold near 1
GeV,
threshold near 1
GeV,  can also go to
can also go to 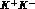 , which in turn can scatter back to
, which in turn can scatter back to 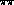 . Though
unitarity still constrains these contributions, one needs information on
. Though
unitarity still constrains these contributions, one needs information on
 and
and 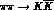 scattering, as well as
scattering, as well as 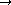
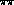 , to know how. This means
it is more
difficult to implement the constraints of unitarity when many channels enter.
However below roughly 1 GeV, elastic unitarity enforces
Watson's theorem [
, to know how. This means
it is more
difficult to implement the constraints of unitarity when many channels enter.
However below roughly 1 GeV, elastic unitarity enforces
Watson's theorem [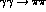 for each I and J,
for each I and J, 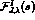 , equal to the
phase of
the corresponding
, equal to the
phase of
the corresponding 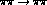 amplitude,
amplitude, 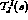 . This is exceedingly useful,
since knowledge
of the phase of an amplitude largely determines the behaviour of its modulus
--- amplitudes being analytic functions. A simple example of this is the phase
rising rapidly from
. This is exceedingly useful,
since knowledge
of the phase of an amplitude largely determines the behaviour of its modulus
--- amplitudes being analytic functions. A simple example of this is the phase
rising rapidly from
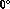 to
to 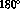 . The modulus then has to peak at a position and width
wholly correlated with the phase variation. This relationship is exemplified
by the
well-known Breit-Wigner formula. The general relation between the phase and
the modulus of the amplitude is embodied in the Omnès representation [
. The modulus then has to peak at a position and width
wholly correlated with the phase variation. This relationship is exemplified
by the
well-known Breit-Wigner formula. The general relation between the phase and
the modulus of the amplitude is embodied in the Omnès representation [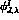 , from
, from
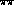 threshold to infinity, we can define a function
threshold to infinity, we can define a function
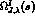 (the Omnès function)
(the Omnès function)
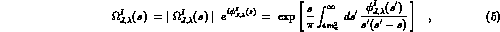
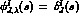 , the
, the 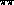 phase shift, independent of the two photon helicity
phase shift, independent of the two photon helicity
 .
This function,
.
This function,  , has the phase
, has the phase  by construction.
The way convergent dispersion relations work,
by construction.
The way convergent dispersion relations work,  at low energies
fortunately does not require detailed knowledge of the phase
at low energies
fortunately does not require detailed knowledge of the phase  above 1 GeV.
We will return to this later.
above 1 GeV.
We will return to this later.
 scattering is explained
in detail
in Ref. 6. Here we sketch the methodology.
We can write an appropriately subtracted dispersion relation for each
partial wave amplitude, specified by I, J and
scattering is explained
in detail
in Ref. 6. Here we sketch the methodology.
We can write an appropriately subtracted dispersion relation for each
partial wave amplitude, specified by I, J and  . For the S-waves
(J=0,
. For the S-waves
(J=0, 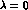 ), these are twice subtracted [
), these are twice subtracted [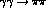 amplitudes above 1 GeV. The lack of knowledge of these
terms is parametrized by two subtraction constants that are fixed by two
crucial low energy constraints. Firstly, Low's theorem that states each partial wave amplitude
equals its corresponding Born term at s=0 --- that follows from QED gauge
invariance. Secondly, from chiral dynamics we have a prediction
in the low energy region for the
amplitude minus its Born term. Thus, for instance the neutral channel
S-wave has a zero at
amplitudes above 1 GeV. The lack of knowledge of these
terms is parametrized by two subtraction constants that are fixed by two
crucial low energy constraints. Firstly, Low's theorem that states each partial wave amplitude
equals its corresponding Born term at s=0 --- that follows from QED gauge
invariance. Secondly, from chiral dynamics we have a prediction
in the low energy region for the
amplitude minus its Born term. Thus, for instance the neutral channel
S-wave has a zero at 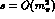 ---
in one loop
Chiral Perturbation Theory (
---
in one loop
Chiral Perturbation Theory (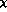 PT ) [
PT ) [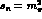 .
In general,
all we know is that these near threshold corrections
are
.
In general,
all we know is that these near threshold corrections
are 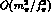 . These low energy limits fix the two
subtraction constants,
. These low energy limits fix the two
subtraction constants, 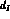 , in the I=0 and 2
, in the I=0 and 2  S-wave amplitudes. Thus
S-wave amplitudes. Thus

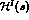 have the complete left hand cut
and no right hand cut. They are given by
have the complete left hand cut
and no right hand cut. They are given by
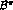 is the one pion exchange Born term and
is the one pion exchange Born term and
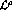 ,
,
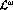 denote the contributions
to the left-hand cut generated by exchanges with
denote the contributions
to the left-hand cut generated by exchanges with 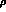 and
and  quantum numbers, respectively.
Then the combinations in the charged and neutral channels are :
quantum numbers, respectively.
Then the combinations in the charged and neutral channels are :
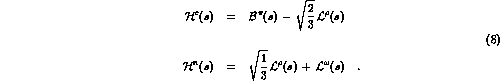
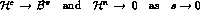 ,
so in turn this means :
,
so in turn this means :
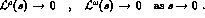 Recalling
Recalling 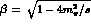 (Eq. (1)), the S-wave
Born amplitude
is, for example, [
(Eq. (1)), the S-wave
Born amplitude
is, for example, [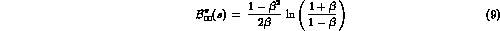
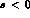 .
.

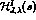 are the appropriate partial waves of the left hand cut
components of Eq. (
are the appropriate partial waves of the left hand cut
components of Eq. (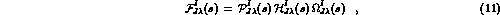
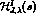 has the left hand cut, Eq. (
has the left hand cut, Eq. (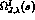 the right hand cut, Eq. (
the right hand cut, Eq. (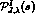 is a
real polynomial. While
is a
real polynomial. While 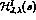 is the full left hand cut function, it is often
convenient to model this function by some
is the full left hand cut function, it is often
convenient to model this function by some 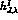 (for instance, the
Born term) and rewrite Eq. (
(for instance, the
Born term) and rewrite Eq. (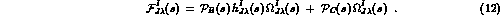
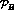 and
and 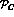 (with
(with 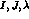 labels suppressed)
may now be more complicated functions along the
left hand cut, but they will continue to be smooth along the right hand cut away from their
singularities. In physical terms, the first term models the simple well
understood cross-channel exchanges and then
labels suppressed)
may now be more complicated functions along the
left hand cut, but they will continue to be smooth along the right hand cut away from their
singularities. In physical terms, the first term models the simple well
understood cross-channel exchanges and then 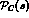 incorporates the
rest as direct channel contributions. Near
incorporates the
rest as direct channel contributions. Near  threshold,
threshold,
 is just the pion exchange Born term and there are
essentially no direct channel effects other than those of final state
interactions automatically included in Eqs. (
is just the pion exchange Born term and there are
essentially no direct channel effects other than those of final state
interactions automatically included in Eqs. (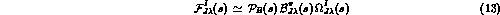
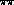 masses, 500 MeV or so, by taking
masses, 500 MeV or so, by taking
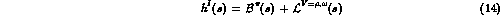
 still zero. However, above
that energy, direct channel effects ( or equivalently heavier mass
cross-channel exchanges ) become increasingly important and definite
predictions possible near threshold must give way to fitting
data [
still zero. However, above
that energy, direct channel effects ( or equivalently heavier mass
cross-channel exchanges ) become increasingly important and definite
predictions possible near threshold must give way to fitting
data [ and
hence the direct channel couplings.
and
hence the direct channel couplings.

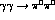 as a function of the
as a function of the  invariant mass,
invariant mass, 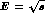 . The data are
from Crystal Ball [
. The data are
from Crystal Ball [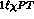 is the prediction of one loop Chiral Perturbation Theory [
is the prediction of one loop Chiral Perturbation Theory [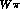 " is the dispersive calculation
using Weinberg phases [
" is the dispersive calculation
using Weinberg phases [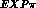 " are the predictions
from experimental
" are the predictions
from experimental  phases
as described in [
phases
as described in [ -exchange
for the left hand cut.
-exchange
for the left hand cut.