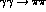 , Fig. 1,
observed in
, Fig. 1,
observed in 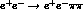 [1],
can be computed exactly with minimal assumptions.
This makes this reaction almost unique among processes in which
important strong interaction effects occur.
[1],
can be computed exactly with minimal assumptions.
This makes this reaction almost unique among processes in which
important strong interaction effects occur.
At low energy the cross-section, integrated
and differential, for the reaction 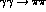 , Fig. 1,
observed in
, Fig. 1,
observed in 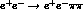 [1],
can be computed exactly with minimal assumptions.
This makes this reaction almost unique among processes in which
important strong interaction effects occur.
[1],
can be computed exactly with minimal assumptions.
This makes this reaction almost unique among processes in which
important strong interaction effects occur.
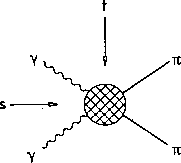
Figure 1: The process  in the
s-channel.
in the
s-channel.
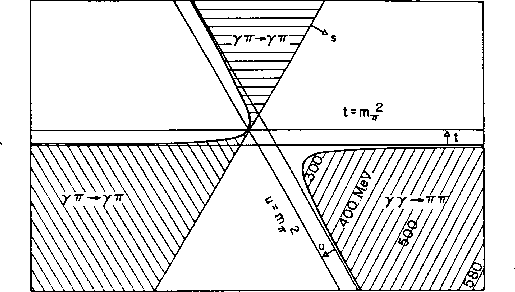
Figure 2: Mandelstam plane showing the three related physical regions.
The
s-channel is  and the t & u-channels are
and the t & u-channels are
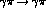 . The pion poles at
. The pion poles at
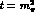 ,
, 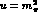 are marked. They cross
at the
are marked. They cross
at the 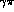 thresholds.
thresholds.
Predictions are possible because Low's low energy theorem [2]
absolutely normalizes the cross-sections at the nearby cross-channel
threshold, Fig. 2. There at the threshold for Compton scattering the
photon just measures the charge of the pion and the amplitude is given
by the Born term, 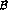 . For
. For 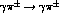 this involves one-pion-exchange [1] and
this involves one-pion-exchange [1] and 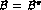 , while for
, while for 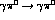 it is zero. Because
the all-important pion pole that determines the Born amplitude is so
very near the
it is zero. Because
the all-important pion pole that determines the Born amplitude is so
very near the 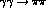 physical region, it also dominates [3,4,6]
the behaviour of the
physical region, it also dominates [3,4,6]
the behaviour of the 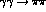 amplitude in the low energy region, Fig. 2.
Thus the amplitude is given by the Born term plus the effect of an
infinite number of other exchanges,
amplitude in the low energy region, Fig. 2.
Thus the amplitude is given by the Born term plus the effect of an
infinite number of other exchanges, 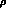 ,
,  ,
, 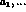 These
exchanges are relatively far from the physical region below 500 MeV in
These
exchanges are relatively far from the physical region below 500 MeV in
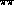 mass and so play a very small role close to threshold.
Indeed, the relative importance of these singularities can be judged
by considering how close the poles of these exchanges are to the
centre of the
mass and so play a very small role close to threshold.
Indeed, the relative importance of these singularities can be judged
by considering how close the poles of these exchanges are to the
centre of the 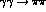 physical region at
physical region at 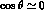 ,
displayed in Figs. 2 and 3. Nearness is all that matters, since their
couplings to
,
displayed in Figs. 2 and 3. Nearness is all that matters, since their
couplings to 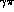 are all of the same order of magnitude.
are all of the same order of magnitude.
Figure 3: Nearness of poles in the t & u-channels
( ) from
) from  ,
,  and
and
 -exchange to the s-channel (
-exchange to the s-channel ( )
physical region,
)
physical region,  , depicted as the
shaded region, at different
, depicted as the
shaded region, at different 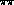 masses.
masses.
That the pion pole does truly dominate can be seen by looking at the
experimental results. Normalized cross-sections for 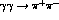 come from
Mark II [7] and CELLO [8]. These are displayed
in Fig. 4. Also shown are the low energy results of
PLUTO [9]. These are in fact for
come from
Mark II [7] and CELLO [8]. These are displayed
in Fig. 4. Also shown are the low energy results of
PLUTO [9]. These are in fact for  at
at 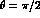 and have been extrapolated to the angular
coverage of Mark II for comparison, assuming the cross-section to be
pure S-wave near threshold
and have been extrapolated to the angular
coverage of Mark II for comparison, assuming the cross-section to be
pure S-wave near threshold ![]() . For the
. For the 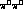 channel, data come from Crystal Ball at DORIS [10], shown in
the lower half of Fig. 4. It is easy to understand these
cross-sections qualitatively : at low energy, the photon, as in the
Compton process, couples to the charge of the pion. This means the
channel, data come from Crystal Ball at DORIS [10], shown in
the lower half of Fig. 4. It is easy to understand these
cross-sections qualitatively : at low energy, the photon, as in the
Compton process, couples to the charge of the pion. This means the
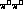 cross-section is small, while that for
cross-section is small, while that for 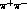 is large ; how large
is determined by the charge of the pion. As the energy increases, the
effective wavelength of the photon shortens and it recognises that the
pions, whether charged or neutral, are made of the same charged
constituents, namely quarks, and causes these to resonate. Thus at
1270 MeV, one sees the well-known tensor resonance, the
is large ; how large
is determined by the charge of the pion. As the energy increases, the
effective wavelength of the photon shortens and it recognises that the
pions, whether charged or neutral, are made of the same charged
constituents, namely quarks, and causes these to resonate. Thus at
1270 MeV, one sees the well-known tensor resonance, the 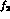 . Tensor
resonances naturally arise in two photon processes (as in radiative
decays of the
. Tensor
resonances naturally arise in two photon processes (as in radiative
decays of the 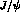 ) since they can couple with no relative orbital
angular momentum to the two spin-one photons. If the
) since they can couple with no relative orbital
angular momentum to the two spin-one photons. If the 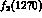 dominates the reactions in this region, one could read off its
dominates the reactions in this region, one could read off its  coupling from the peak height of these cross-sections : that in
coupling from the peak height of these cross-sections : that in  and
and  being related by an isospin Clebsch-Gordan coefficient.
However, life is not so simple. Analysis of the angular distribution
allows a large S-wave signal under the
being related by an isospin Clebsch-Gordan coefficient.
However, life is not so simple. Analysis of the angular distribution
allows a large S-wave signal under the
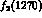 [11,8], associated with the
[11,8], associated with the
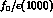 (which is the same state as the
(which is the same state as the 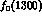 of
the PDG tables [12]). It is the couplings of the
of
the PDG tables [12]). It is the couplings of the 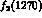 and of the
and of the  to
to  , with a small effect from the
, with a small effect from the
 , that are the outcome of experiments from 600 to 1400
MeV in
, that are the outcome of experiments from 600 to 1400
MeV in 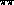 mass, as we discuss later.
mass, as we discuss later.
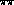 production, initiated by two very nearly real photons, can by
Bose symmetry have isospin zero and two. G-parity means
these pions are in an even spin state. In charged
pion production, the two isospin amplitudes constructively interfere, while in
production, initiated by two very nearly real photons, can by
Bose symmetry have isospin zero and two. G-parity means
these pions are in an even spin state. In charged
pion production, the two isospin amplitudes constructively interfere, while in
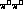 production they destructively interfere. It is this that
makes the two cross-sections so different at low energies, Fig. 4. Thus
unusually for a hadronic
reaction, the isospin two interaction is as strong as that with isospin zero
at low energies. This is a consequence of pion pole dominance. Away from
threshold, this is no longer the case, when I=0 resonances enter the
scattering process. Nevertheless, this emphasizes how measurements of both
production they destructively interfere. It is this that
makes the two cross-sections so different at low energies, Fig. 4. Thus
unusually for a hadronic
reaction, the isospin two interaction is as strong as that with isospin zero
at low energies. This is a consequence of pion pole dominance. Away from
threshold, this is no longer the case, when I=0 resonances enter the
scattering process. Nevertheless, this emphasizes how measurements of both
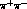 and
and 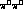 cross-sections are
needed to be able to separate the
cross-sections are
needed to be able to separate the 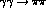 cross-section into its
isospin components.
cross-section into its
isospin components.
Figure 4:
(a) 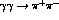 cross-section
for
cross-section
for 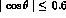 from Mark II [7] , CELLO [8] and
PLUTO [9] --- the last
of these
is only shown at low
from Mark II [7] , CELLO [8] and
PLUTO [9] --- the last
of these
is only shown at low 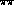 mass
where the experimental results on
mass
where the experimental results on 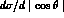 at
at
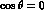 can be
scaled to give
can be
scaled to give  for
for 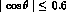 assuming a flat
distribution ;
(b)
assuming a flat
distribution ;
(b) 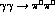 cross-section for
cross-section for
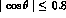 from Crystal Ball [10]
(labelled Marsiske)
and the higher
statistics, higher mass data (labelled Karch) tabulated in the data review by
Morgan et al. [1].
from Crystal Ball [10]
(labelled Marsiske)
and the higher
statistics, higher mass data (labelled Karch) tabulated in the data review by
Morgan et al. [1].
Both are as
functions of 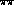 invariant mass.
invariant mass.
The photons scatter with either their helicities parallel or anti-parallel, so
the observables are specified by two helicity amplitudes [1]
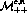 and
and
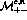 , where c denotes charged pion production and n
neutral. With unpolarised beams one only measures the sum of the
squares of the moduli of these amplitudes, so at a
, where c denotes charged pion production and n
neutral. With unpolarised beams one only measures the sum of the
squares of the moduli of these amplitudes, so at a  c.m. energy
of
c.m. energy
of 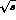 the differential cross-sections are :
the differential cross-sections are :
where 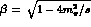 with
with 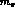 appropriately the charged or neutral pion mass.
The helicity amplitudes can be partial wave projected
to give the components,
appropriately the charged or neutral pion mass.
The helicity amplitudes can be partial wave projected
to give the components, 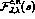 , with
, with 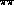 spin J and helicity
spin J and helicity  (=0
or
2) with even
(=0
or
2) with even 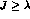 , defined by :
, defined by :
where the factor of 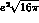 has been taken out for later
convenience. With this
normalization the integrated cross-sections are
has been taken out for later
convenience. With this
normalization the integrated cross-sections are
These amplitudes and their
partial waves are combinations of amplitudes with definite 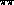 isospin I,
isospin I, 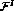 , in terms of which
the amplitudes for the
physical processes
, in terms of which
the amplitudes for the
physical processes 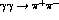 and
and 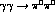 are
are ![]() :
:
Note once more that the one-pion exchange Born term contributes to both isospin amplitudes.