
For our first estimates, we consider only the first order terms in a partial wave expansion of the form factors F, G and H, i.e., we take

This is consistent with the parametrization used by Pais and Treiman, [4] and Rosselet et al. [5] They consider higher order terms, but the coefficients of these terms are found to be consistent with zero by the experiment of Rosselet et al., [5] so we do not consider further terms in our initial estimates.
All the  and
and 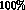
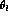 dependence in the problem is
contained in the expression of
dependence in the problem is
contained in the expression of 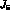 as a function of
these variables and the
as a function of
these variables and the  ; for this reason these
two variables are referred to as ``trivial.''
; for this reason these
two variables are referred to as ``trivial.'' 
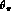 \
appears only in the equations
for the
\
appears only in the equations
for the 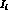 in terms of F, G, and H (and the phase space
expansion, should we consider higher order terms).
This leaves then
in terms of F, G, and H (and the phase space
expansion, should we consider higher order terms).
This leaves then 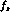 , g and h with a possible
dependence on s_
, g and h with a possible
dependence on s_ 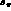 and s_l
and s_l 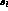 . The
. The 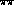 phase
shifts
phase
shifts  and
and 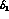 (which at this order
appear only in the combination
(which at this order
appear only in the combination 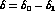 )
depend only on s_
)
depend only on s_ 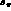 . For the moment we parametrize
. For the moment we parametrize
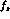 , g and h by an expression of the form
, g and h by an expression of the form
where 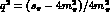 s_
s_ 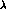 , and y stands
for f, g, or h. We take
the slope
, and y stands
for f, g, or h. We take
the slope 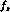 to be the same for
to be the same for 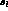 , g
and h, and no slope in s_l
, g
and h, and no slope in s_l 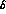 at this stage, again
consistent with Ref. [5]. For the dependence of
at this stage, again
consistent with Ref. [5]. For the dependence of 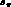 on s_
on s_ 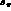 we will consider average values in a set of
5 bins in s_
we will consider average values in a set of
5 bins in s_ 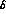 , and consider parametrizations of
, and consider parametrizations of 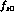 in a later section.
in a later section.
One last important detail remains to be mentioned. The
MLM (or asymmetries, for that matter) says nothing about
an overall factor in the intensity, as we require the
probability density to be normalized to one. Thus we
divide out 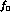 (
(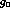 for short) from the amplitude, as it
is the parameter with the most effect on the integrated intensity.
Wherever
for short) from the amplitude, as it
is the parameter with the most effect on the integrated intensity.
Wherever 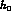 and
and 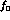 appear, they are divided by
appear, they are divided by 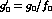 ,
so we replace them by new parameters
,
so we replace them by new parameters
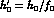 and
and 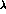 (
( and
and  are unaffected). We then apply the MLM
to the set of parameters
are unaffected). We then apply the MLM
to the set of parameters 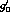 ,
, 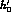 ,
, 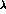 and
and 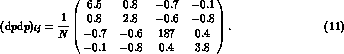 ,
and obtain the correlation matrix
,
and obtain the correlation matrix

The diagonal entries of this matrix are variances of the four parameters, where N is the number of events. The off-diagonal elements represent correlations between the parameters; in this case they are small, but they can be significant, depending on the parametrization used. We do not report the full correlation matrix for each parametrization in this paper, but they are available from our programs if needed for further calculations. They can not be neglected in general if one wants to calculate functions of the parameters we use, and propagate the errors correctly. In the end of this paper, we consider the determination of some highly correlated parameters.
We then extract the error on  from the equation
from the equation

where  is the unnormalized probability function
inputted to the MLM calculation, and C represents all the
constant factors (masses, two's,
is the unnormalized probability function
inputted to the MLM calculation, and C represents all the
constant factors (masses, two's, 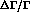 's) needed to complete
the equation. The relative error
's) needed to complete
the equation. The relative error 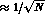 is
given by
is
given by 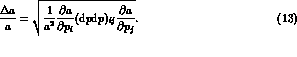 in an experiment like
KLOE [6]
where the statistical error will be dominant.
The relative error on the integral (a) is given by the matrix
product
in an experiment like
KLOE [6]
where the statistical error will be dominant.
The relative error on the integral (a) is given by the matrix
product

Combining this error in quadrature with the statistical error on
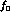 , we obtain the error we quote for
, we obtain the error we quote for 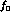 ; combining
the error on
; combining
the error on 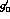 in quadrature with the errors on
in quadrature with the errors on 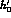 and
and 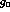 ,
we obtain the errors we quote for
,
we obtain the errors we quote for 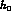 and
and 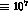 .
.
In Table 1 we display the results of this calculation.
The central values (our input) are those found by the previous
experiment. [5]
We have used the program VEGAS [7]
to do the necessary integrals in five-dimensional phase space.
The normalization of the probability distribution is ensured
automatically by the program, and the necessary derivatives
also computed numerically.
Estimated errors are shown for
N=30000 events, the statistics of the previous experiment)
and N=300000 events, the anticipated statistics [1]
in one ``year''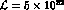 seconds
of running with
seconds
of running with 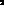 cm
cm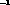 s
s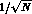 .
All errors in this paper, unless otherwise noted, are statistical
errors and can be simply scaled by
.
All errors in this paper, unless otherwise noted, are statistical
errors and can be simply scaled by 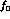 for different
numbers of events. As a general rule, also, the fractional
error on
for different
numbers of events. As a general rule, also, the fractional
error on 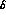 is roughly
independent of its central value, while the
absolute errors of the other
parameters remain constant. The last line of Table 1 shows the errors on
these parameters found by Rosselet et al..
We do not quote the error on
is roughly
independent of its central value, while the
absolute errors of the other
parameters remain constant. The last line of Table 1 shows the errors on
these parameters found by Rosselet et al..
We do not quote the error on  because an error on
because an error on
 averaged over the whole of phase space is not very
meaningful. The errors shown are independent of the central value
of
averaged over the whole of phase space is not very
meaningful. The errors shown are independent of the central value
of 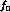 used.
used.
Table 1: Central values and estimated errors
for 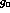 ,
, 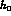 ,
,  and
and 
At this point, before going on to further discuss errors in KLOE, it is
necessary to say some words about why our estimated errors at
``Rosselet statistics'' are so different from those that Rosselet quotes.
The errors given above are purely statistical, but apply to a
``perfect'' detector, i.e., one which covers the whole of phase space with
unity efficiency everywhere.
This is close
to true for KLOE; we will attempt to illustrate this later in this
paper, and will describe a more rigorous demonstration in
a future paper. However, Rosselet's detector was far from ``perfect.''
In the error we have quoted for 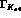 , the errors from
, the errors from 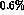 and the normalization a contribute about equally; the first is
about
and the normalization a contribute about equally; the first is
about 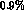 and the second about
and the second about 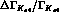 . Rosselet, however,
quotes a relative error
. Rosselet, however,
quotes a relative error 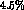 K_e4
K_e4 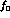 of
of
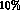 , which completely accounts for their large error on
, which completely accounts for their large error on 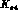 .
Their fixed target experiment had a
.
Their fixed target experiment had a 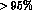 overall efficiency for K_e4
overall efficiency for K_e4 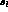 ,
and a highly variable efficiency as well, varying, for example,
smoothly from
,
and a highly variable efficiency as well, varying, for example,
smoothly from 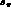 in a very small portion of phase space with
large s_l
in a very small portion of phase space with
large s_l 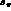 and small s_
and small s_ 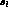 , to near zero at large s_
, to near zero at large s_ 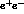 and small s_l
and small s_l 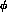 .
KLOE is in contrast a hermetic detector, operating at a
.
KLOE is in contrast a hermetic detector, operating at a 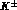 collider running at the
collider running at the 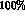 resonance, producing self-tagging
low momentum
resonance, producing self-tagging
low momentum  pairs. It will have a uniform near-
pairs. It will have a uniform near- efficiency over all of phase space, minus a few percent of phase
space that will be cleanly cut and discarded. [8]
efficiency over all of phase space, minus a few percent of phase
space that will be cleanly cut and discarded. [8]
The next step in our analysis was to drop the slope parameter
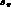 and determine the errors on the parameters in five
bins in s_
and determine the errors on the parameters in five
bins in s_ 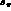 , chosen so as to have equal numbers of events. Such
an analysis with real data would have the advantages of studying
the s_
, chosen so as to have equal numbers of events. Such
an analysis with real data would have the advantages of studying
the s_  dependence in a more parametrization
independent way. If, however,
the s_
dependence in a more parametrization
independent way. If, however,
the s_ 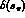 dependence is correctly given by eq. 10, this method
will not determine
dependence is correctly given by eq. 10, this method
will not determine  as accurately, so in general both
types of approach are necessary. For our purposes, displaying the
error in bins is also important to illustrate the possible accuracies
with which
as accurately, so in general both
types of approach are necessary. For our purposes, displaying the
error in bins is also important to illustrate the possible accuracies
with which 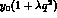 may be measured, before we implement a possible
parametrization of
may be measured, before we implement a possible
parametrization of 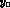 . In Table 2, we give the estimated
errors, taking an average of
. In Table 2, we give the estimated
errors, taking an average of  in each bin
as our inputs for y=f, g, and h, with Rosselet values for
the
in each bin
as our inputs for y=f, g, and h, with Rosselet values for
the 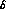 and
and  . The errors on
. The errors on 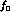 are essentially independent of the inputs of its central value.
In the last line, for comparison, we display the errors
on
are essentially independent of the inputs of its central value.
In the last line, for comparison, we display the errors
on 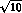 as measured by Rosselet et al. The improvement
is not as drastic as that of
as measured by Rosselet et al. The improvement
is not as drastic as that of 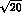 was, but is nonetheless a factor of
1.5 to 2. This should be further multiplied by a factor of
was, but is nonetheless a factor of
1.5 to 2. This should be further multiplied by a factor of
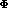 to
to 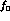 per DA
per DA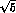 NE running year.
The accuracy on f in bins is even better than we might have
expected from the error on
NE running year.
The accuracy on f in bins is even better than we might have
expected from the error on 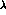 multiplied by
multiplied by 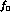 . This
is because the error on
. This
is because the error on  gives most of the contribution
to the error on the normalization a, and thus a significant
contribution to the error on
gives most of the contribution
to the error on the normalization a, and thus a significant
contribution to the error on 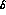 .
.

Table 2: Estimated errors in five bins of 6000 events each.
We have examined in some detail the question of what accuracy
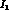 can be measured to. We have first of all determined
that while
can be measured to. We have first of all determined
that while 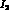 appears in
appears in 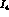 ,
, 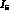 ,
, 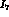 ,
, 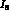 ,
,
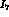 , and
, and  , it is only the dependence of
, it is only the dependence of 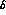 that
gives us the above accuracy on
that
gives us the above accuracy on  . This can be seen
by replacing
. This can be seen
by replacing  in all the
in all the  , except
, except 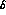 , by
a dummy variable
, by
a dummy variable 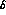 , set equal to the central value
of
, set equal to the central value
of 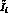 . When we proceed to apply the MLM to the new
probability function, we find the same error on
. When we proceed to apply the MLM to the new
probability function, we find the same error on 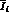 as before, within a few percent. If, however, we apply
the MLM to the
as before, within a few percent. If, however, we apply
the MLM to the 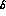 as parameters in their own right
(we cannot use the
as parameters in their own right
(we cannot use the 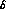 as parameters, because they are
functions of the phase space variables) and then take the
ratio to determine
as parameters, because they are
functions of the phase space variables) and then take the
ratio to determine 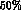 , we find that the error on
, we find that the error on  increases by
increases by 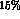 . (If we use the asymmetry method to
determine the
. (If we use the asymmetry method to
determine the 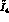 , the error increases another
, the error increases another 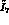 .)
We have not taken care to cancel
correlated errors in
.)
We have not taken care to cancel
correlated errors in 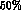 and
and 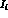 ,
but we have checked that
the correlated parts of the errors are small relative to the
uncorrelated parts.
So, this
,
but we have checked that
the correlated parts of the errors are small relative to the
uncorrelated parts.
So, this 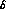 increase appears to be mainly due to the information
lost in integrating the
increase appears to be mainly due to the information
lost in integrating the 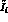 over three out of five of the
phase space variables before applying the MLM. Equivalently,
the better error on
over three out of five of the
phase space variables before applying the MLM. Equivalently,
the better error on 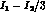 can be attributed to applying
a more detailed parametrization (therefore more information)
from the beginning of the calculation.
can be attributed to applying
a more detailed parametrization (therefore more information)
from the beginning of the calculation.
Nonetheless, it may be interesting to determine the 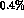 and
their errors
as a parameterization independent way to present
the data. We have estimated that the combination
and
their errors
as a parameterization independent way to present
the data. We have estimated that the combination 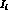 can be determined to
can be determined to  in five bins of 60,000 events each.
The other
in five bins of 60,000 events each.
The other  can be determined with absolute errors of
one to two times this error.
can be determined with absolute errors of
one to two times this error.