


Next: 4 Other parametrizations
Up: Chapter 7 Section 4
Previous: Estimating experimental uncertainties
So far we have estimated the statistical experimental uncertainties
in a perfect detector. In this section we would like to say a few
words about other experimental uncertainties.
Errors (other than those already estimated) in a detector like KLOE,
where the efficiency is essentially 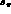 outside of a small
region of phase space to be removed by cuts, fall into two categories:
those associated with cuts, and those associated with resolution.
We intend to write an event generator, that would allow us to
impose a proper cut
on true kinematical variables such as the angles of the particles
themselves, or their momenta,
but for the moment are only
calculating the MLM error estimating integral
over s_l
outside of a small
region of phase space to be removed by cuts, fall into two categories:
those associated with cuts, and those associated with resolution.
We intend to write an event generator, that would allow us to
impose a proper cut
on true kinematical variables such as the angles of the particles
themselves, or their momenta,
but for the moment are only
calculating the MLM error estimating integral
over s_l 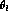 , s_
, s_ 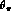 ,
, 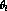
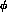 ,
, 
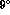 and
and 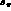 .
We expect that [8]
appropriate cuts will be applied
to reject charged particles that have momenta
less than 20 MeV, and those that are within
.
We expect that [8]
appropriate cuts will be applied
to reject charged particles that have momenta
less than 20 MeV, and those that are within 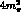 of being
parallel to the beam pipe (because they will not cross enough
wires). We expect that both of these cuts will (from the point of
view of our problem) reject events fairly randomly, and thus only
have the effect of reducing the number of events by a couple of
percent, having a negligible effect on our error estimates.
Just to check, we have considered cutting
of being
parallel to the beam pipe (because they will not cross enough
wires). We expect that both of these cuts will (from the point of
view of our problem) reject events fairly randomly, and thus only
have the effect of reducing the number of events by a couple of
percent, having a negligible effect on our error estimates.
Just to check, we have considered cutting 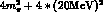 in the range
in the range
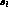 to
to  , and
, and  in the range 0 to
in the range 0 to 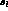 . The s_
. The s_ 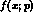 cut has negligible
effect and the s_l
cut has negligible
effect and the s_l  cut increases our errors by about 10 percent
or less. Eventually we would also like to investigate the
effect of inaccurate cuts (for example a cut that is believed to
be at 20 MeV and is really at 15 MeV), which can be an important
source of systematic errors.
cut increases our errors by about 10 percent
or less. Eventually we would also like to investigate the
effect of inaccurate cuts (for example a cut that is believed to
be at 20 MeV and is really at 15 MeV), which can be an important
source of systematic errors.
Smearing, also known as convolution with a resolution function,
can be imposed on our variables with more confidence, being a random
effect. We assume a gaussian resolution function, i.e., we
replace the probability function  by a
new function
by a
new function 

where y is a dummy variable introduced to make the gaussian
integrable,  and
and 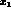 .
.
 and
and  are the lower and upper bounds on x;
are the lower and upper bounds on x;
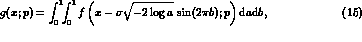 is assumed to be large compared to
is assumed to be large compared to 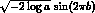 .
Thus we have
.
Thus we have

showing the equivalence of convolution with a
gaussian and integrating after a gaussian
smearing of
the independent variable. Note that the quantity
 , for a and b uniformly distributed
in the interval 0 to 1, is gaussian distributed with variance 1.
, for a and b uniformly distributed
in the interval 0 to 1, is gaussian distributed with variance 1.
KLOE expects a resolution of about half a
percent to one percent in angles and momenta. We make the assumption
that smearing by one percent (of 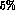 or
or 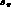 in the case of
our angles) in our five variables is a reasonable and generous
approximation
to smearing in the actual kinematic variables. We observe negligible
effect on our errors; in fact smearing of as much as
in the case of
our angles) in our five variables is a reasonable and generous
approximation
to smearing in the actual kinematic variables. We observe negligible
effect on our errors; in fact smearing of as much as
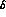 of the maximum
of our variables has no effect except in
of the maximum
of our variables has no effect except in 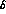 , where it yields
a ten percent (fractional!)
increase in our errors. This is not surprising.
If one knows one's resolution function, one can compensate
for it, and the accuracy is unaffected, at least if the scale of the
smearing is small compared to the scale of the effect (this scale
in our case is of the order of
the whole of phase space). If however
there are unknown parts to the resolution function, i.e.,
systematic errors, these can result in systematic errors
in the result, that the MLM error estimating technique above will
never find, simply because we have no way to input an unknown
error. These errors could in principle be estimated by applying
the MLM itself to simulated data, but this is beyond the scope of
our investigation. The accurate estimation of systematic errors
is at any rate something that will have to be done by KLOE.
Meanwhile, however, we have made one attempt
to estimate the effect of such systematic
errors by returning to the determination of
, where it yields
a ten percent (fractional!)
increase in our errors. This is not surprising.
If one knows one's resolution function, one can compensate
for it, and the accuracy is unaffected, at least if the scale of the
smearing is small compared to the scale of the effect (this scale
in our case is of the order of
the whole of phase space). If however
there are unknown parts to the resolution function, i.e.,
systematic errors, these can result in systematic errors
in the result, that the MLM error estimating technique above will
never find, simply because we have no way to input an unknown
error. These errors could in principle be estimated by applying
the MLM itself to simulated data, but this is beyond the scope of
our investigation. The accurate estimation of systematic errors
is at any rate something that will have to be done by KLOE.
Meanwhile, however, we have made one attempt
to estimate the effect of such systematic
errors by returning to the determination of  from the
asymmetry method. Here we can easily calculate what
from the
asymmetry method. Here we can easily calculate what
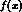 we would ``measure'' from an imaginary set of data
described by a set of input parameters; normally of course, we
get back the value of
we would ``measure'' from an imaginary set of data
described by a set of input parameters; normally of course, we
get back the value of 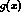 we input. If, however, we replace
the probability distribution
we input. If, however, we replace
the probability distribution 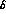 by a convoluted distribution
by a convoluted distribution
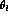 , then,
by the shift in the recovered
, then,
by the shift in the recovered 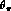 , we can see what would
be the effect of a resolution function that we did not know about,
and therefore did not compensate for.
, we can see what would
be the effect of a resolution function that we did not know about,
and therefore did not compensate for.
We have first verified that gaussian smearing still has no
significant effect, which means that it is not
neccessary to know the exact form of the resolution
function, as long as it is symmetric and not too broad
in the appropriate scale.
We have next examined the effect of an actual shift in each
of our phase space variables. The effect is tiny compared
to the statistical errors for shifts in 
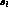 ,
, 
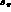 , s_l
, s_l 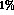 \
and s_
\
and s_ 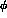 . For a
. For a 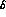 shift in
shift in 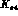 ,
, 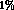 goes down
by 0.01, or about half of the statistical error with
300,000 K_e4
goes down
by 0.01, or about half of the statistical error with
300,000 K_e4 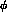 events. We remark that a
events. We remark that a 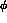 systematic
shift in
systematic
shift in 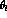 is already so large as to be inconcievable,
as
is already so large as to be inconcievable,
as 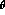 is a difference of observable angles.
is a difference of observable angles.



Next: 4 Other parametrizations
Up: Chapter 7 Section 4
Previous: Estimating experimental uncertainties
Carlos E.Piedrafita
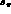 outside of a small
region of phase space to be removed by cuts, fall into two categories:
those associated with cuts, and those associated with resolution.
We intend to write an event generator, that would allow us to
impose a proper cut
on true kinematical variables such as the angles of the particles
themselves, or their momenta,
but for the moment are only
calculating the MLM error estimating integral
over s_l
outside of a small
region of phase space to be removed by cuts, fall into two categories:
those associated with cuts, and those associated with resolution.
We intend to write an event generator, that would allow us to
impose a proper cut
on true kinematical variables such as the angles of the particles
themselves, or their momenta,
but for the moment are only
calculating the MLM error estimating integral
over s_l 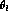 , s_
, s_ 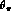 ,
, 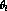
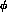 ,
, 
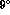 and
and 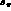 .
We expect that [8]
appropriate cuts will be applied
to reject charged particles that have momenta
less than 20 MeV, and those that are within
.
We expect that [8]
appropriate cuts will be applied
to reject charged particles that have momenta
less than 20 MeV, and those that are within 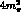 of being
parallel to the beam pipe (because they will not cross enough
wires). We expect that both of these cuts will (from the point of
view of our problem) reject events fairly randomly, and thus only
have the effect of reducing the number of events by a couple of
percent, having a negligible effect on our error estimates.
Just to check, we have considered cutting
of being
parallel to the beam pipe (because they will not cross enough
wires). We expect that both of these cuts will (from the point of
view of our problem) reject events fairly randomly, and thus only
have the effect of reducing the number of events by a couple of
percent, having a negligible effect on our error estimates.
Just to check, we have considered cutting 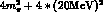 in the range
in the range
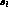 to
to  , and
, and  in the range 0 to
in the range 0 to 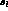 . The s_
. The s_ 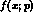 cut has negligible
effect and the s_l
cut has negligible
effect and the s_l 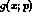 cut increases our errors by about 10 percent
or less. Eventually we would also like to investigate the
effect of inaccurate cuts (for example a cut that is believed to
be at 20 MeV and is really at 15 MeV), which can be an important
source of systematic errors.
cut increases our errors by about 10 percent
or less. Eventually we would also like to investigate the
effect of inaccurate cuts (for example a cut that is believed to
be at 20 MeV and is really at 15 MeV), which can be an important
source of systematic errors.
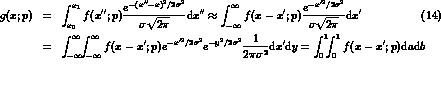 by a
new function
by a
new function 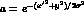

 and
and  .
.
 and
and  are the lower and upper bounds on x;
are the lower and upper bounds on x;
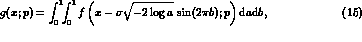 is assumed to be large compared to
is assumed to be large compared to 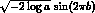 .
Thus we have
.
Thus we have

 , for a and b uniformly distributed
in the interval 0 to 1, is gaussian distributed with variance 1.
, for a and b uniformly distributed
in the interval 0 to 1, is gaussian distributed with variance 1.
 or
or  in the case of
our angles) in our five variables is a reasonable and generous
approximation
to smearing in the actual kinematic variables. We observe negligible
effect on our errors; in fact smearing of as much as
in the case of
our angles) in our five variables is a reasonable and generous
approximation
to smearing in the actual kinematic variables. We observe negligible
effect on our errors; in fact smearing of as much as
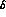 of the maximum
of our variables has no effect except in
of the maximum
of our variables has no effect except in 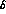 , where it yields
a ten percent (fractional!)
increase in our errors. This is not surprising.
If one knows one's resolution function, one can compensate
for it, and the accuracy is unaffected, at least if the scale of the
smearing is small compared to the scale of the effect (this scale
in our case is of the order of
the whole of phase space). If however
there are unknown parts to the resolution function, i.e.,
systematic errors, these can result in systematic errors
in the result, that the MLM error estimating technique above will
never find, simply because we have no way to input an unknown
error. These errors could in principle be estimated by applying
the MLM itself to simulated data, but this is beyond the scope of
our investigation. The accurate estimation of systematic errors
is at any rate something that will have to be done by KLOE.
Meanwhile, however, we have made one attempt
to estimate the effect of such systematic
errors by returning to the determination of
, where it yields
a ten percent (fractional!)
increase in our errors. This is not surprising.
If one knows one's resolution function, one can compensate
for it, and the accuracy is unaffected, at least if the scale of the
smearing is small compared to the scale of the effect (this scale
in our case is of the order of
the whole of phase space). If however
there are unknown parts to the resolution function, i.e.,
systematic errors, these can result in systematic errors
in the result, that the MLM error estimating technique above will
never find, simply because we have no way to input an unknown
error. These errors could in principle be estimated by applying
the MLM itself to simulated data, but this is beyond the scope of
our investigation. The accurate estimation of systematic errors
is at any rate something that will have to be done by KLOE.
Meanwhile, however, we have made one attempt
to estimate the effect of such systematic
errors by returning to the determination of  from the
asymmetry method. Here we can easily calculate what
from the
asymmetry method. Here we can easily calculate what
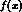 we would ``measure'' from an imaginary set of data
described by a set of input parameters; normally of course, we
get back the value of
we would ``measure'' from an imaginary set of data
described by a set of input parameters; normally of course, we
get back the value of 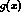 we input. If, however, we replace
the probability distribution
we input. If, however, we replace
the probability distribution 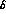 by a convoluted distribution
by a convoluted distribution
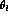 , then,
by the shift in the recovered
, then,
by the shift in the recovered 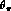 , we can see what would
be the effect of a resolution function that we did not know about,
and therefore did not compensate for.
, we can see what would
be the effect of a resolution function that we did not know about,
and therefore did not compensate for.

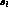 ,
, 
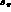 , s_l
, s_l 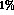 \
and s_
\
and s_ 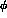 . For a
. For a 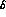 shift in
shift in 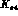 ,
, 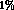 goes down
by 0.01, or about half of the statistical error with
300,000 K_e4
goes down
by 0.01, or about half of the statistical error with
300,000 K_e4 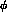 events. We remark that a
events. We remark that a 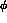 systematic
shift in
systematic
shift in 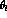 is already so large as to be inconcievable,
as
is already so large as to be inconcievable,
as 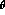 is a difference of observable angles.
is a difference of observable angles.