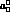 dependence in f, g, etc.;
(3) we consider two parametrizations of
dependence in f, g, etc.;
(3) we consider two parametrizations of 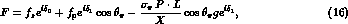 in terms
of s-wave scattering length
in terms
of s-wave scattering length 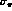 to
give a first indication on what errors can be expected on this
parameter.
to
give a first indication on what errors can be expected on this
parameter.
In this section we would like to present results
for some extensions of the minimal parametrization we have used
so far: (1) we include a p-wave term in F, and simultaneously
adopt a notation consistent with the partial wave expansion of
Ref. [1]; (2) we consider an 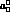 dependence in f, g, etc.;
(3) we consider two parametrizations of
dependence in f, g, etc.;
(3) we consider two parametrizations of 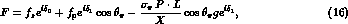 in terms
of s-wave scattering length
in terms
of s-wave scattering length 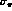 to
give a first indication on what errors can be expected on this
parameter.
to
give a first indication on what errors can be expected on this
parameter.
F thus becomes

where 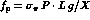 ,
,  and X are defined in Ref. [1].
Our previous parametrization is thus equivalent to this one
for
and X are defined in Ref. [1].
Our previous parametrization is thus equivalent to this one
for 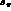 .
For the
.
For the 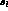 dependence, chiral perturbation theory to one loop
predicts [9]
approximately the same slope for s_
dependence, chiral perturbation theory to one loop
predicts [9]
approximately the same slope for s_ 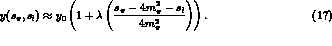 and s_l
and s_l  , or, more precisely,
, or, more precisely,

To be more model-independent, and to have a separate determination
of the s_ 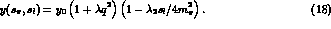 and s_l
and s_l 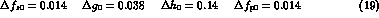 slopes, we choose the parametrization
slopes, we choose the parametrization
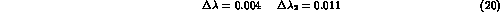
We then find, for 300000 events,


to be compared with table 1. We have displayed the errors for
the old parameters as well as the added ones, as some of them
have increased slightly. We have taken central values
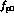 and
and 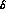 (which maintains the normalization
unchanged); if other parameters are preferred it should be remembered
that the absolute errors of
(which maintains the normalization
unchanged); if other parameters are preferred it should be remembered
that the absolute errors of  and the
slope remain essentially constant.
and the
slope remain essentially constant.
For 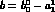 we have first considered the parametrization
used [10]
by the previous experiment, to compare our estimated errors
with the ones they determined. They use
we have first considered the parametrization
used [10]
by the previous experiment, to compare our estimated errors
with the ones they determined. They use
where  , the difference between the s-wave slope
and the p-wave scattering length. There is moreover
a possible relation between b and
, the difference between the s-wave slope
and the p-wave scattering length. There is moreover
a possible relation between b and 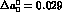
For 30000 events (to compare with Ref. [5]) we find
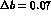 , to be compared with 0.05 in Ref. [5],
if we use both eqs. 21 and 22.
If we use only eq. 21 we find
, to be compared with 0.05 in Ref. [5],
if we use both eqs. 21 and 22.
If we use only eq. 21 we find 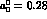 and
and
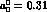 , to be compared with 0.11 and 0.16 in
Ref. [5]. We have used the central values
, to be compared with 0.11 and 0.16 in
Ref. [5]. We have used the central values 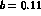 in
the first case, and
in
the first case, and  ,
, 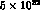 in the second case,
as found in Ref. [5]. So, in one year running at DA
in the second case,
as found in Ref. [5]. So, in one year running at DA NE at
a luminosity of
NE at
a luminosity of 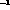 cm
cm s
s , we
expect a factor of five improvement in the error on the
, we
expect a factor of five improvement in the error on the
 scattering length, meaning that DA
scattering length, meaning that DA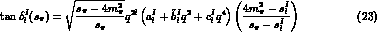 NE should be able
to determine if the existing discrepancy
between measurements and predictions for
NE should be able
to determine if the existing discrepancy
between measurements and predictions for 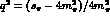 is statistically
significant.
is statistically
significant.
We have also considered a more recent parametrization, due to Schenk. [11] He gives
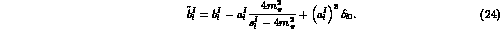
where 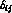 s_
s_  and
and

Here I denotes isospin, l angular momentum, and 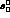 is the
Kronecker delta. We need to calculate
is the
Kronecker delta. We need to calculate 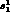 and
and 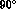 ;
;  and
and 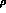 (the values at which the phase shifts should pass through
(the values at which the phase shifts should pass through 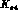 )
are the squares of the
)
are the squares of the  and
and 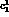 meson masses.
There are far too many parameters here to be able to
determine them
by K_e4
meson masses.
There are far too many parameters here to be able to
determine them
by K_e4 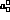 measurements alone; to begin with, we fix the higher order
coefficients
measurements alone; to begin with, we fix the higher order
coefficients 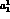 and
and 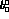 to zero.
The remaining set
to zero.
The remaining set 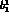 ,
, 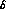 ,
, 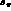 and
and 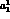 is still too large: if we plot
is still too large: if we plot  versus s_
versus s_ 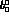 , we find that
while changing
, we find that
while changing  from its central value of 0.037 to a new
value of 0.087 changes
from its central value of 0.037 to a new
value of 0.087 changes 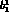 essentially uniformly by 15
percent, changing instead
essentially uniformly by 15
percent, changing instead 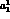 from its central value of 0.24
to 0.19 has the same effect, to within about 1 percent.
Moreover, with appropriate variations in
from its central value of 0.24
to 0.19 has the same effect, to within about 1 percent.
Moreover, with appropriate variations in 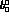 and
and 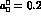 ,
one can quite well mock up a variation in
,
one can quite well mock up a variation in 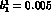 (or
(or  ,
naturally).
Thus, one can only hope to determine two independent parameters
without recourse to other experiments or other theoretical constraints.
,
naturally).
Thus, one can only hope to determine two independent parameters
without recourse to other experiments or other theoretical constraints.
The MLM quantifies these conclusions. Assuming Schenk's central
values (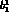 ,
, 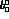 , and above),
, and above), 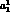 or
or  can be determined to 0.03 (for Rosselet statistics of 30,000 events),
or
can be determined to 0.03 (for Rosselet statistics of 30,000 events),
or 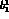 or
or  to 0.04, if only one parameter is considered, and
the rest held fixed. If one determines
to 0.04, if only one parameter is considered, and
the rest held fixed. If one determines 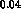 and
and 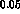 simultaneously,
holding the rest of the parameters fixed,
the correlation is 0.71 (defined as the covariance of the two parameters
divided by the
simultaneously,
holding the rest of the parameters fixed,
the correlation is 0.71 (defined as the covariance of the two parameters
divided by the 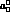 's
for each, 1 for a maximally correlated pair of
variables), and the errors are
's
for each, 1 for a maximally correlated pair of
variables), and the errors are 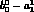 and
and 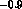 respectively.
If one determines instead
respectively.
If one determines instead 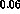 and
and 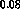 simultaneously,
the correlation is
simultaneously,
the correlation is 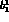 and the errors are
and the errors are 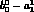 and
and 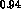 ;
for
;
for 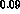 and
and 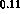 the correlation is
the correlation is 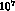 and the
errors are
and the
errors are 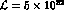 and
and  . To determine more than two parameters
simultaneously is not possible.
. To determine more than two parameters
simultaneously is not possible.