


Next: Estimating experimental uncertainties
Up: Chapter 7 Section 4
Previous: Chapter 7 Section 4
In this contribution to the DA NE physics handbook, we estimate the
accuracies achievable at DA
NE physics handbook, we estimate the
accuracies achievable at DA NE in measuring the theoretical
parameters describing the decay
NE in measuring the theoretical
parameters describing the decay 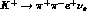 .
We refer the reader to the contribution of Bijnens, Ecker, and
Gasser [1]
for a detailed discussion of the theory of this decay,
and the definitions of the notation we use.
We should note that we refer to this decay as K_e4
.
We refer the reader to the contribution of Bijnens, Ecker, and
Gasser [1]
for a detailed discussion of the theory of this decay,
and the definitions of the notation we use.
We should note that we refer to this decay as K_e4 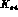 ; we
consider only this particular decay and not the channels with
neutral pions or kaons.
; we
consider only this particular decay and not the channels with
neutral pions or kaons.
We will consider two of the possible ways
of extracting the parameters of a theory from a set of data.
The first one is the classic technique of asymmetries.
K_e4 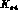 decays have a partial
decay rate
decays have a partial
decay rate  of the form
of the form
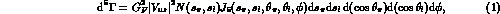
where s_ 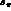 , s_l
, s_l 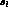 ,
, 
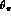 ,
, 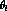
 , and
, and  are the set of
kinematic variables necessary to describe K_e4
are the set of
kinematic variables necessary to describe K_e4 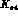 , defined in
Ref. [1].
The quantity
, defined in
Ref. [1].
The quantity 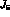 can be written as an expansion in simple
functions of
can be written as an expansion in simple
functions of  and
and 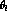
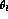 multiplying nine
intensities
multiplying nine
intensities 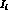 , which can in turn be written in
terms of the three remaining kinematical variables, and three
form factors, F, G, and H, which are also dependent on
these three kinematical variables.
The explicit dependences may be
found in Ref. [1].
As can be seen in the contribution of Colangelo, Knecht and
Stern, [2] the
tangent of the phase shift,
, which can in turn be written in
terms of the three remaining kinematical variables, and three
form factors, F, G, and H, which are also dependent on
these three kinematical variables.
The explicit dependences may be
found in Ref. [1].
As can be seen in the contribution of Colangelo, Knecht and
Stern, [2] the
tangent of the phase shift,  ,
can be neatly extracted from the ratio of the intensity
functions,
,
can be neatly extracted from the ratio of the intensity
functions, 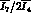 , or, equivalently,
, or, equivalently,
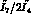 , where by the tilde we denote
intensities integrated over
, where by the tilde we denote
intensities integrated over 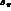 and
and 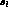 as well
as over
as well
as over 
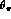 .
All of the
.
All of the 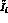 , in
turn, can be written as asymmetries; in particular we have
, in
turn, can be written as asymmetries; in particular we have
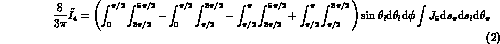
and
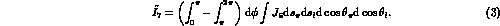
The asymmetry presents a transparent, elegant and quick
(computationally) way to determine a parameter.
The second, and main, method we consider is that of the maximum
likelihood, which we shall refer to as the MLM. [3]
Let  be the vector of phase space variables specifying
an event in an experiment, and
be the vector of phase space variables specifying
an event in an experiment, and 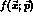 be the
probability distribution function predicted by a theory.
be the
probability distribution function predicted by a theory.
 is the set of parameters in the theory, to
be determined experimentally. The probability of observing
an event at
is the set of parameters in the theory, to
be determined experimentally. The probability of observing
an event at  in the interval
in the interval 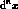 is
is
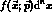 . The function f is normalized
to 1 over the whole
. The function f is normalized
to 1 over the whole  interval in which
interval in which  is physical. In particular, if cuts are imposed on the phase space,
f must be normalized over the reduced phase space; we must
also be certain that the normalization is maintained even when
the parameters are varied from their central value.
is physical. In particular, if cuts are imposed on the phase space,
f must be normalized over the reduced phase space; we must
also be certain that the normalization is maintained even when
the parameters are varied from their central value.
The likelihood,
or joint probability distribution, of an experiment yielding
N events, each
specified by a set of phase space variables 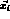 , is
then defined as
, is
then defined as
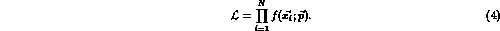
The best estimate for  is then simply the value
is then simply the value
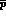 which maximizes
which maximizes 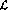 (or equivalently, of
(or equivalently, of
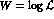 , which is easier to compute).
It can be shown that the error matrix, in general non-diagonal
for correlated parameters, is
, which is easier to compute).
It can be shown that the error matrix, in general non-diagonal
for correlated parameters, is
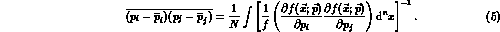
Here the 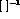 denote matrix inversion. This integral
is, in general, not possible to compute analytically, but is
easily evaluated numerically.
If we start with a non-normalized
probability function
denote matrix inversion. This integral
is, in general, not possible to compute analytically, but is
easily evaluated numerically.
If we start with a non-normalized
probability function  ,
then the following equation is useful:
,
then the following equation is useful:
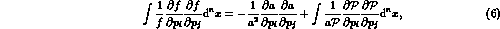
where 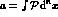 .
.
While this method is more complicated and time-consuming
computationally, it has the decided advantage that it
yields the absolute best possible determination of any
given set of parameters. In today's age of fast computers,
it is thus the method of choice. It also allows one to
determine any parameters chosen, while the asymmetry
is only good for certain parameters. Finally, the
experimental uncertainties in the parameters
can be determined reasonably easily, without need for an
actual simulation of the determination of the parameters
themselves using this method.
It is simple to see that the MLM should give a better
determination of the parameters than an asymmetry:
while the asymmetry only uses the information of
whether an event is in one or another half of phase
space, the MLM benefits from the information of the
precise position of the event. For example, consider
a process specified by the probability distribution
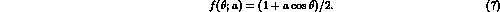
The parameter a can be determined by the ratio
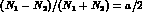 where
where 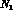 is the number of events
with
is the number of events
with  between 0 and
between 0 and 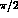 , and
, and
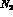 is the number of events
with
is the number of events
with  between
between 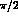 and
and  .
For a small compared to 1, the error on a in this
determination is thus
.
For a small compared to 1, the error on a in this
determination is thus 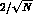 where N is the total
number of events.
For the MLM, the integral in eq. 5 is
where N is the total
number of events.
For the MLM, the integral in eq. 5 is
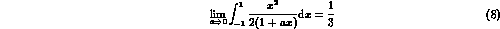
and the error on a in this determination is thus
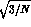 . While this improvement may not seem
very impressive, larger improvements may be expected
as the parametrization becomes more complicated.
Using the MLM directly on the parameter that interests us,
we are sure to use all possible information,
and to take into account the effect of all possible
cancelling uncertainties.
We observe an improvement as above, of about fifteen
percent, in the relative error
. While this improvement may not seem
very impressive, larger improvements may be expected
as the parametrization becomes more complicated.
Using the MLM directly on the parameter that interests us,
we are sure to use all possible information,
and to take into account the effect of all possible
cancelling uncertainties.
We observe an improvement as above, of about fifteen
percent, in the relative error 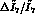 when we go from the asymmetry method to the MLM.
However, the relative error
on
when we go from the asymmetry method to the MLM.
However, the relative error
on 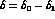 when
when  is determined
directly via the MLM is two-thirds of its error when
determined indirectly by the ratio
is determined
directly via the MLM is two-thirds of its error when
determined indirectly by the ratio
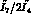 , if these
, if these 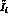 are determined using the MLM, and their errors are then combined
as uncorrelated. This appears to be due to the information
lost in integrating the
are determined using the MLM, and their errors are then combined
as uncorrelated. This appears to be due to the information
lost in integrating the 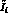 over s_
over s_ 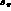 , s_l
, s_l 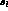 , and
, and 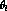
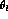 \
before using the MLM.
\
before using the MLM.



Next: Estimating experimental uncertainties
Up: Chapter 7 Section 4
Previous: Chapter 7 Section 4
Carlos E.Piedrafita
 NE physics handbook, we estimate the
accuracies achievable at DA
NE physics handbook, we estimate the
accuracies achievable at DA NE in measuring the theoretical
parameters describing the decay
NE in measuring the theoretical
parameters describing the decay 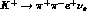 .
We refer the reader to the contribution of Bijnens, Ecker, and
Gasser [1]
for a detailed discussion of the theory of this decay,
and the definitions of the notation we use.
We should note that we refer to this decay as K_e4
.
We refer the reader to the contribution of Bijnens, Ecker, and
Gasser [1]
for a detailed discussion of the theory of this decay,
and the definitions of the notation we use.
We should note that we refer to this decay as K_e4 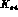 ; we
consider only this particular decay and not the channels with
neutral pions or kaons.
; we
consider only this particular decay and not the channels with
neutral pions or kaons.
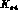 decays have a partial
decay rate
decays have a partial
decay rate  of the form
of the form
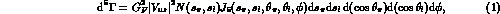
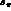 , s_l
, s_l 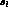 ,
, 
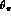 ,
, 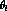
 , and
, and  are the set of
kinematic variables necessary to describe K_e4
are the set of
kinematic variables necessary to describe K_e4 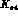 , defined in
Ref. [
, defined in
Ref. [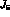 can be written as an expansion in simple
functions of
can be written as an expansion in simple
functions of  and
and 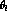
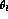 multiplying nine
intensities
multiplying nine
intensities 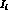 , which can in turn be written in
terms of the three remaining kinematical variables, and three
form factors, F, G, and H, which are also dependent on
these three kinematical variables.
The explicit dependences may be
found in Ref. [
, which can in turn be written in
terms of the three remaining kinematical variables, and three
form factors, F, G, and H, which are also dependent on
these three kinematical variables.
The explicit dependences may be
found in Ref. [ ,
can be neatly extracted from the ratio of the intensity
functions,
,
can be neatly extracted from the ratio of the intensity
functions, 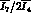 , or, equivalently,
, or, equivalently,
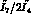 , where by the tilde we denote
intensities integrated over
, where by the tilde we denote
intensities integrated over 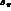 and
and 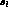 as well
as over
as well
as over 
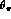 .
All of the
.
All of the 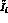 , in
turn, can be written as asymmetries; in particular we have
, in
turn, can be written as asymmetries; in particular we have
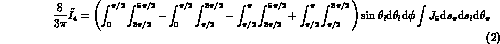
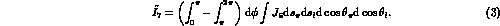
 be the vector of phase space variables specifying
an event in an experiment, and
be the vector of phase space variables specifying
an event in an experiment, and 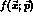 be the
probability distribution function predicted by a theory.
be the
probability distribution function predicted by a theory.
 is the set of parameters in the theory, to
be determined experimentally. The probability of observing
an event at
is the set of parameters in the theory, to
be determined experimentally. The probability of observing
an event at  in the interval
in the interval 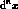 is
is
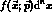 . The function f is normalized
to 1 over the whole
. The function f is normalized
to 1 over the whole  interval in which
interval in which  is physical. In particular, if cuts are imposed on the phase space,
f must be normalized over the reduced phase space; we must
also be certain that the normalization is maintained even when
the parameters are varied from their central value.
is physical. In particular, if cuts are imposed on the phase space,
f must be normalized over the reduced phase space; we must
also be certain that the normalization is maintained even when
the parameters are varied from their central value.
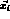 , is
then defined as
, is
then defined as
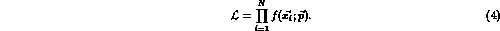
 is then simply the value
is then simply the value
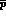 which maximizes
which maximizes 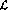 (or equivalently, of
(or equivalently, of
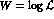 , which is easier to compute).
It can be shown that the error matrix, in general non-diagonal
for correlated parameters, is
, which is easier to compute).
It can be shown that the error matrix, in general non-diagonal
for correlated parameters, is
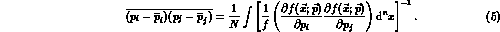
 denote matrix inversion. This integral
is, in general, not possible to compute analytically, but is
easily evaluated numerically.
If we start with a non-normalized
probability function
denote matrix inversion. This integral
is, in general, not possible to compute analytically, but is
easily evaluated numerically.
If we start with a non-normalized
probability function  ,
then the following equation is useful:
,
then the following equation is useful:
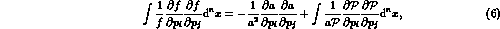
 .
.
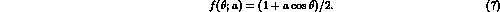
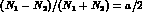 where
where 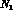 is the number of events
with
is the number of events
with  between 0 and
between 0 and 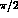 , and
, and
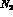 is the number of events
with
is the number of events
with  between
between 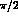 and
and  .
For a small compared to 1, the error on a in this
determination is thus
.
For a small compared to 1, the error on a in this
determination is thus 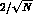 where N is the total
number of events.
For the MLM, the integral in eq.
where N is the total
number of events.
For the MLM, the integral in eq. 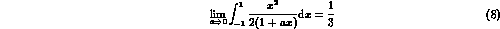
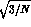 . While this improvement may not seem
very impressive, larger improvements may be expected
as the parametrization becomes more complicated.
Using the MLM directly on the parameter that interests us,
we are sure to use all possible information,
and to take into account the effect of all possible
cancelling uncertainties.
We observe an improvement as above, of about fifteen
percent, in the relative error
. While this improvement may not seem
very impressive, larger improvements may be expected
as the parametrization becomes more complicated.
Using the MLM directly on the parameter that interests us,
we are sure to use all possible information,
and to take into account the effect of all possible
cancelling uncertainties.
We observe an improvement as above, of about fifteen
percent, in the relative error 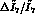 when we go from the asymmetry method to the MLM.
However, the relative error
on
when we go from the asymmetry method to the MLM.
However, the relative error
on 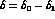 when
when  is determined
directly via the MLM is two-thirds of its error when
determined indirectly by the ratio
is determined
directly via the MLM is two-thirds of its error when
determined indirectly by the ratio
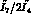 , if these
, if these 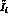 are determined using the MLM, and their errors are then combined
as uncorrelated. This appears to be due to the information
lost in integrating the
are determined using the MLM, and their errors are then combined
as uncorrelated. This appears to be due to the information
lost in integrating the 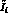 over s_
over s_ 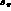 , s_l
, s_l 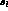 , and
, and 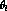
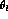 \
before using the MLM.
\
before using the MLM.