


Next: 5 Values of the
Up: Chapter 4 Section 3
Previous: 3 Expansion of the
The difference between standard and generalized 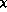 PT merely concerns the
symmetry breaking sector of the theory. In the chiral limit
PT merely concerns the
symmetry breaking sector of the theory. In the chiral limit 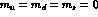 ,
observables described by purely derivative terms of the effective Lagrangian
,
observables described by purely derivative terms of the effective Lagrangian
 are essentially given by
soft pion theorems which are identical in both schemes. This concerns, in
particular, the electromagnetic radius of the pion, the decay
are essentially given by
soft pion theorems which are identical in both schemes. This concerns, in
particular, the electromagnetic radius of the pion, the decay  , the
, the 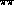 scattering in the P-wave, the leading order
scattering in the P-wave, the leading order  and
and  form-factors, etc...
form-factors, etc...
The difficulty of disentangling both schemes resides in the fact that
symmetry breaking effects are small and not well known experimentally. In this
section we are going to give an overview of the main differences
between the predictions
of standard and generalized  PT for symmetry breaking effects which
already appear at the leading order
PT for symmetry breaking effects which
already appear at the leading order 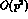 . Those have more chances to be
observable, at least indirectly.
. Those have more chances to be
observable, at least indirectly.
4a -  : Dismiss of the ellipse [14]
: Dismiss of the ellipse [14]
We have already stressed the importance of the quark mass ratio
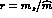 as an independent parameter of G
as an independent parameter of G PT. When isospin
breaking is switched on, G
PT. When isospin
breaking is switched on, G PT leads to a relation between the two quark
mass ratios r and R, with
PT leads to a relation between the two quark
mass ratios r and R, with
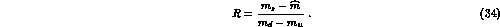
Taking a suitable linear combination of the expansions of 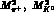 and
and 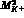 , the
, the 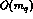 terms, the
terms, the 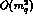 terms and even the
terms and even the 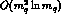 terms drop out and one obtains
[4]
terms drop out and one obtains
[4]

where 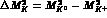 is the kaon mass difference in the
absence of electromagnetism. Eq. (35) holds independently of the value of r,
i.e. both in the standard and in the generalized
is the kaon mass difference in the
absence of electromagnetism. Eq. (35) holds independently of the value of r,
i.e. both in the standard and in the generalized 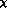 PT. In
the standard case, Eq. (35)
should be rather accurate, whereas in the generalized setting the
neglected
PT. In
the standard case, Eq. (35)
should be rather accurate, whereas in the generalized setting the
neglected 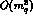 terms - arising from
terms - arising from  and given by the
low energy constants
and given by the
low energy constants  (27) - can easily represent a 30% correction.
(27) - can easily represent a 30% correction.
To the best of our knowledge, Eq. (35) has
never appeared in the literature on standard
 PT. Instead, one rather expands ratios of pseudoscalar meson masses
and one eliminates the
PT. Instead, one rather expands ratios of pseudoscalar meson masses
and one eliminates the 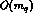 terms from this expansion (see e.g. Eqs. (10.11)
and (10.17) of the second of Refs. [2]). In this
way, one arrives at the well known
elliptic relation between
terms from this expansion (see e.g. Eqs. (10.11)
and (10.17) of the second of Refs. [2]). In this
way, one arrives at the well known
elliptic relation between 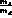 and
and 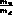 , extensively
commented upon in the literature [14]. The difference between
the two procedures
is instructive : When expanding the linear
combinations of pseudoscalar meson
masses, one expands in powers of the small parameter
, extensively
commented upon in the literature [14]. The difference between
the two procedures
is instructive : When expanding the linear
combinations of pseudoscalar meson
masses, one expands in powers of the small parameter
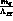 . On
the other hand, when expanding mass ratios, one assumes, in addition,
that the
parameter
. On
the other hand, when expanding mass ratios, one assumes, in addition,
that the
parameter 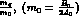 is also small.
Actually, the elliptic relation [14] should read
is also small.
Actually, the elliptic relation [14] should read
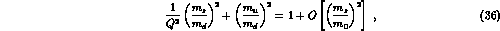
where
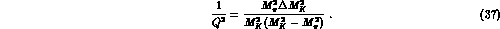
The quark mass ratios lie on the ellipse only provided  or,
equivalently, provided
or,
equivalently, provided 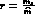 is close to
is close to 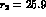 , whereas
Eq. (35) has a more general validity.
, whereas
Eq. (35) has a more general validity.
It is interesting to look at Eq. (35) in the light
of recent discussions of a
possible large violation of Dashen's theorem [15]. We can write

where the parameter 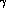 describes the departure from Dashen's theorem
:
describes the departure from Dashen's theorem
:  if the theorem is exact. Various recent estimates [15]
expect
if the theorem is exact. Various recent estimates [15]
expect
 somewhere between 1 and 2. Taking in Eq. (35)
somewhere between 1 and 2. Taking in Eq. (35)
 , one obtains
R=43 for
, one obtains
R=43 for 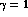 and
and  for
for 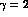 . For r=10, Eq. (35)
predicts R=66 if
. For r=10, Eq. (35)
predicts R=66 if 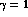 , whereas R=53 if
, whereas R=53 if  . Assuming
. Assuming 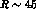 (as expected from baryon masses and from
(as expected from baryon masses and from  mixing [9])
we observe that
by increasing
mixing [9])
we observe that
by increasing 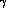 , we are left with less room for
, we are left with less room for 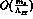 corrections to Eq. (35), which could provide a
valuable information on the
corrections to Eq. (35), which could provide a
valuable information on the  parameters
parameters 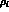 .
.

4b - Quark condensates for 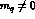
The parameter 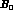 describes the quark condensate in the chiral limit
describes the quark condensate in the chiral limit
 . The leading order Lagrangian
. The leading order Lagrangian 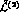 allows to
express
allows to
express 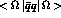 , where
, where 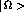 is the ground
state for
is the ground
state for 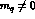 , beyond this limit. One gets
, beyond this limit. One gets
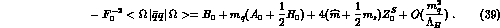
where q=u,d,s denotes a given quark flavour. The point is that if
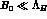 , the
, the 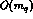 contribution is Eq. (39) can
be relatively
important. Comparing for instance the term
contribution is Eq. (39) can
be relatively
important. Comparing for instance the term 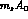 to
to 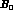 one finds, using
Eqs. (26a) and (26b),
one finds, using
Eqs. (26a) and (26b),  , assuming r=10 and
, assuming r=10 and 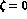 . This
should not be surprising : in G
. This
should not be surprising : in G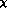 PT all contributions of
PT all contributions of
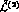 are supposed to be of the same order of magnitude. In
practice, it implies that the
are supposed to be of the same order of magnitude. In
practice, it implies that the  condensates can exhibit a large
flavour dependence. Unfortunately, there is no way to pin down the constant
condensates can exhibit a large
flavour dependence. Unfortunately, there is no way to pin down the constant
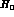 which controls this dependence quantitatively :
which controls this dependence quantitatively : 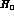 is not a low energy
order parameter, but rather a short distance counterterm (see Ref. [2]
for a discussion of this point).
is not a low energy
order parameter, but rather a short distance counterterm (see Ref. [2]
for a discussion of this point).
4c - Large corrections to the soft pion theorems
Within generalized 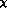 PT the corrections to soft pion theorems can
sometimes be rather important - of the same order as the soft pion result
itself. Consider, for instance, the scalar form factor of the pion at
vanishing momentum transfer or, equivalently, the pion
PT the corrections to soft pion theorems can
sometimes be rather important - of the same order as the soft pion result
itself. Consider, for instance, the scalar form factor of the pion at
vanishing momentum transfer or, equivalently, the pion  -term
-term

The soft pion result for  is well known :
is well known :

Since in the G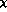 PT,
PT, 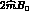 can be considerably smaller
than
can be considerably smaller
than 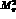 , one might be tempted to conclude, on the basis of the
soft pion result (41), that in G
, one might be tempted to conclude, on the basis of the
soft pion result (41), that in G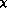 PT
PT 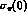 is
smaller than in
the standard theory. This conclusion does not take into account all
is
smaller than in
the standard theory. This conclusion does not take into account all
 contributions to
contributions to 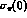 described by
described by  .
Writing
.
Writing 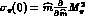 ,
using Eqs. (5) and (26), and neglecting the Zweig rule violating parameter
,
using Eqs. (5) and (26), and neglecting the Zweig rule violating parameter
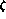 , one obtains the correct
, one obtains the correct  result,
result,
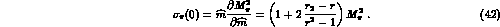
It is seen that, when r decreases from 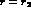 to
to 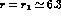 , the
pion
, the
pion  -term increases from
-term increases from 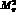 to
to 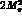 . In G
. In G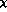 PT,
the soft pion result will receive a large correction, whenever the soft pion
theorem result is proportional to the quark condensate
PT,
the soft pion result will receive a large correction, whenever the soft pion
theorem result is proportional to the quark condensate  . The
reason is that both
. The
reason is that both 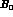 and
and  count as quantities of order
count as quantities of order 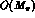 . The formalism of
G
. The formalism of
G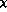 PT automatically takes care of such large corrections. This phenomenon
can in principle lead to modifications of the standard evaluation of the
non-leptonic K-decay matrix elements in the large
PT automatically takes care of such large corrections. This phenomenon
can in principle lead to modifications of the standard evaluation of the
non-leptonic K-decay matrix elements in the large 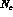 limit, in particular,
of the penguin-contribution to the ratio
limit, in particular,
of the penguin-contribution to the ratio
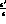 [16].
[16].
There is another relevant example of a similar nature : The 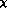 PT
prediction for the low
PT
prediction for the low  behavior of the spectral function associated
with the divergence of the axial current,
behavior of the spectral function associated
with the divergence of the axial current,

At low 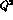 , the continuum part of
, the continuum part of 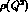 is dominated by the
contribution of
is dominated by the
contribution of 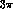 intermediate states. Using for the latter the soft pion
theorem (and neglecting in the phase space integral (43) the pion mass) one
gets the standard result [17]
intermediate states. Using for the latter the soft pion
theorem (and neglecting in the phase space integral (43) the pion mass) one
gets the standard result [17]
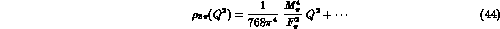
Within the 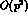 G
G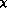 PT, this result is considerably modified. Still
neglecting the pion mass in the phase space integral (in order to facilitate a
comparison with the standard result) one gets [18]
PT, this result is considerably modified. Still
neglecting the pion mass in the phase space integral (in order to facilitate a
comparison with the standard result) one gets [18]

As r decreases from 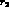 down to
down to  , the enhancement factor in Eq.
(45)
increases from 1 to 13.5. This enhancement would considerably affect the
existing estimates of
, the enhancement factor in Eq.
(45)
increases from 1 to 13.5. This enhancement would considerably affect the
existing estimates of  using the QCD sum rules [17].
using the QCD sum rules [17].
4d -  and
and  scattering
scattering
Our last example of a leading order difference between the standard and the
generalized  PT is of a direct experimental relevance: It concerns the low
energy
PT is of a direct experimental relevance: It concerns the low
energy 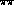 [4] and
[4] and  [5] scattering. The
[5] scattering. The 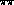 amplitude
predicted by the leading order G
amplitude
predicted by the leading order G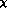 PT lagrangian
PT lagrangian 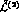 reads
reads
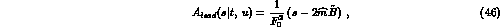
where

is the non strange quark antiquark condensate in the SU(2) SU(2) chiral
limit (see Eq. (39)). Eq. (46) holds both in the standard case and
in the genertalized
SU(2) chiral
limit (see Eq. (39)). Eq. (46) holds both in the standard case and
in the genertalized 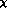 PT. In the standard case, however,
PT. In the standard case, however, 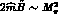 , and one recovers the well known formula first
obtained by Weinberg [19]. In G
, and one recovers the well known formula first
obtained by Weinberg [19]. In G PT, this formula is modified
already at
the leading order
PT, this formula is modified
already at
the leading order 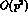 :
:  can be considerably
smaller than
can be considerably
smaller than 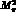 by an amount which depends on r. For r decreasing
from
by an amount which depends on r. For r decreasing
from  =25.9 to r=6.3,
=25.9 to r=6.3,  decreases from
decreases from 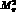 to zero. The low energy
to zero. The low energy  scattering thus provides us with a
quasi-unique experimental access to the order parameter
scattering thus provides us with a
quasi-unique experimental access to the order parameter 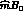 . The
corresponding G
. The
corresponding G PT predictions, endowed with the necessary loop
corrections, are presented in detail in the section on
PT predictions, endowed with the necessary loop
corrections, are presented in detail in the section on  interactions of
the present Handbook.
interactions of
the present Handbook.
A similar conclusion holds in the case of 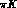 scattering [5]. The
latter gives
a contribution to the
scattering [5]. The
latter gives
a contribution to the 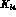 form factor R, which is measurable in the
form factor R, which is measurable in the
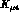 decay mode. Whereas the leading order predictions for the
decay mode. Whereas the leading order predictions for the 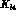 form factors F, G and H are identical in both schemes, there is a
detectable difference in the leading order expression for R [5].
Whether
this difference can be observed in practice is presently under investigation
[25].
form factors F, G and H are identical in both schemes, there is a
detectable difference in the leading order expression for R [5].
Whether
this difference can be observed in practice is presently under investigation
[25].



Next: 5 Values of the
Up: Chapter 4 Section 3
Previous: 3 Expansion of the
Carlos E.Piedrafita
 PT merely concerns the
symmetry breaking sector of the theory. In the chiral limit
PT merely concerns the
symmetry breaking sector of the theory. In the chiral limit 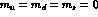 ,
observables described by purely derivative terms of the effective Lagrangian
,
observables described by purely derivative terms of the effective Lagrangian
 are essentially given by
soft pion theorems which are identical in both schemes. This concerns, in
particular, the electromagnetic radius of the pion, the decay
are essentially given by
soft pion theorems which are identical in both schemes. This concerns, in
particular, the electromagnetic radius of the pion, the decay  , the
, the 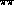 scattering in the P-wave, the leading order
scattering in the P-wave, the leading order  and
and  form-factors, etc...
form-factors, etc...
 PT for symmetry breaking effects which
already appear at the leading order
PT for symmetry breaking effects which
already appear at the leading order 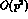 . Those have more chances to be
observable, at least indirectly.
. Those have more chances to be
observable, at least indirectly.
 : Dismiss of the ellipse [
: Dismiss of the ellipse [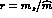 as an independent parameter of G
as an independent parameter of G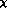 PT. When isospin
breaking is switched on, G
PT. When isospin
breaking is switched on, G PT leads to a relation between the two quark
mass ratios r and R, with
PT leads to a relation between the two quark
mass ratios r and R, with
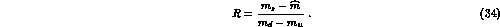
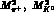 and
and 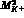 , the
, the 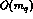 terms, the
terms, the 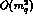 terms and even the
terms and even the 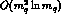 terms drop out and one obtains
[
terms drop out and one obtains
[
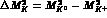 is the kaon mass difference in the
absence of electromagnetism. Eq. (35) holds independently of the value of r,
i.e. both in the standard and in the generalized
is the kaon mass difference in the
absence of electromagnetism. Eq. (35) holds independently of the value of r,
i.e. both in the standard and in the generalized 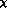 PT. In
the standard case, Eq. (
PT. In
the standard case, Eq. (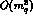 terms - arising from
terms - arising from  and given by the
low energy constants
and given by the
low energy constants  (
( PT. Instead, one rather expands ratios of pseudoscalar meson masses
and one eliminates the
PT. Instead, one rather expands ratios of pseudoscalar meson masses
and one eliminates the 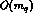 terms from this expansion (see e.g. Eqs. (10.11)
and (10.17) of the second of Refs. [
terms from this expansion (see e.g. Eqs. (10.11)
and (10.17) of the second of Refs. [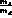 and
and 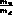 , extensively
commented upon in the literature [
, extensively
commented upon in the literature [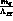 . On
the other hand, when expanding mass ratios, one assumes, in addition,
that the
parameter
. On
the other hand, when expanding mass ratios, one assumes, in addition,
that the
parameter 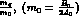 is also small.
Actually, the elliptic relation [
is also small.
Actually, the elliptic relation [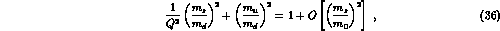
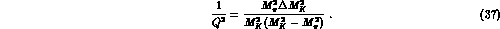
 or,
equivalently, provided
or,
equivalently, provided 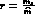 is close to
is close to 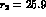 , whereas
Eq. (
, whereas
Eq. (
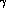 describes the departure from Dashen's theorem
:
describes the departure from Dashen's theorem
:  if the theorem is exact. Various recent estimates [
if the theorem is exact. Various recent estimates [ somewhere between 1 and 2. Taking in Eq. (
somewhere between 1 and 2. Taking in Eq. ( , one obtains
R=43 for
, one obtains
R=43 for 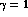 and
and  for
for 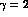 . For r=10, Eq. (
. For r=10, Eq. (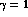 , whereas R=53 if
, whereas R=53 if  . Assuming
. Assuming 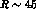 (as expected from baryon masses and from
(as expected from baryon masses and from  mixing [
mixing [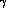 , we are left with less room for
, we are left with less room for 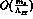 corrections to Eq. (
corrections to Eq. ( parameters
parameters 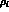 .
.

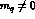
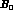 describes the quark condensate in the chiral limit
describes the quark condensate in the chiral limit
 . The leading order Lagrangian
. The leading order Lagrangian 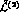 allows to
express
allows to
express 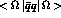 , where
, where 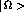 is the ground
state for
is the ground
state for 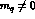 , beyond this limit. One gets
, beyond this limit. One gets
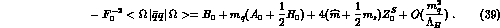
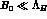 , the
, the 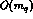 contribution is Eq. (
contribution is Eq. (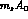 to
to 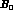 one finds, using
Eqs. (26a) and (26b),
one finds, using
Eqs. (26a) and (26b),  , assuming r=10 and
, assuming r=10 and 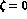 . This
should not be surprising : in G
. This
should not be surprising : in G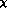 PT all contributions of
PT all contributions of
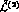 are supposed to be of the same order of magnitude. In
practice, it implies that the
are supposed to be of the same order of magnitude. In
practice, it implies that the  condensates can exhibit a large
flavour dependence. Unfortunately, there is no way to pin down the constant
condensates can exhibit a large
flavour dependence. Unfortunately, there is no way to pin down the constant
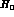 which controls this dependence quantitatively :
which controls this dependence quantitatively : 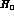 is not a low energy
order parameter, but rather a short distance counterterm (see Ref. [
is not a low energy
order parameter, but rather a short distance counterterm (see Ref. [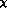 PT the corrections to soft pion theorems can
sometimes be rather important - of the same order as the soft pion result
itself. Consider, for instance, the scalar form factor of the pion at
vanishing momentum transfer or, equivalently, the pion
PT the corrections to soft pion theorems can
sometimes be rather important - of the same order as the soft pion result
itself. Consider, for instance, the scalar form factor of the pion at
vanishing momentum transfer or, equivalently, the pion  -term
-term

 is well known :
is well known :

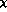 PT,
PT, 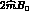 can be considerably smaller
than
can be considerably smaller
than 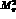 , one might be tempted to conclude, on the basis of the
soft pion result (
, one might be tempted to conclude, on the basis of the
soft pion result (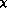 PT
PT 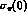 is
smaller than in
the standard theory. This conclusion does not take into account all
is
smaller than in
the standard theory. This conclusion does not take into account all
 contributions to
contributions to 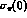 described by
described by  .
Writing
.
Writing 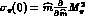 ,
using Eqs. (
,
using Eqs. (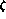 , one obtains the correct
, one obtains the correct  result,
result,
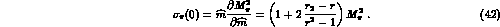
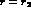 to
to 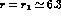 , the
pion
, the
pion  -term increases from
-term increases from 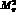 to
to 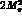 . In G
. In G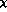 PT,
the soft pion result will receive a large correction, whenever the soft pion
theorem result is proportional to the quark condensate
PT,
the soft pion result will receive a large correction, whenever the soft pion
theorem result is proportional to the quark condensate  . The
reason is that both
. The
reason is that both 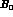 and
and  count as quantities of order
count as quantities of order 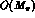 . The formalism of
G
. The formalism of
G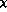 PT automatically takes care of such large corrections. This phenomenon
can in principle lead to modifications of the standard evaluation of the
non-leptonic K-decay matrix elements in the large
PT automatically takes care of such large corrections. This phenomenon
can in principle lead to modifications of the standard evaluation of the
non-leptonic K-decay matrix elements in the large 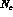 limit, in particular,
of the penguin-contribution to the ratio
limit, in particular,
of the penguin-contribution to the ratio
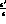 [
[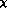 PT
prediction for the low
PT
prediction for the low  behavior of the spectral function associated
with the divergence of the axial current,
behavior of the spectral function associated
with the divergence of the axial current,

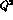 , the continuum part of
, the continuum part of 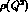 is dominated by the
contribution of
is dominated by the
contribution of 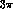 intermediate states. Using for the latter the soft pion
theorem (and neglecting in the phase space integral (
intermediate states. Using for the latter the soft pion
theorem (and neglecting in the phase space integral (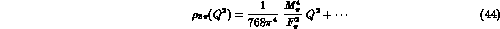
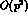 G
G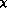 PT, this result is considerably modified. Still
neglecting the pion mass in the phase space integral (in order to facilitate a
comparison with the standard result) one gets [
PT, this result is considerably modified. Still
neglecting the pion mass in the phase space integral (in order to facilitate a
comparison with the standard result) one gets [
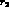 down to
down to  , the enhancement factor in Eq.
(
, the enhancement factor in Eq.
( using the QCD sum rules [
using the QCD sum rules [ and
and  scattering
scattering
 PT is of a direct experimental relevance: It concerns the low
energy
PT is of a direct experimental relevance: It concerns the low
energy 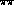 [
[ [
[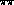 amplitude
predicted by the leading order G
amplitude
predicted by the leading order G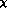 PT lagrangian
PT lagrangian 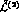 reads
reads
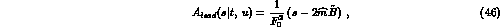

 SU(2) chiral
limit (see Eq. (
SU(2) chiral
limit (see Eq. (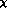 PT. In the standard case, however,
PT. In the standard case, however, 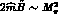 , and one recovers the well known formula first
obtained by Weinberg [
, and one recovers the well known formula first
obtained by Weinberg [ PT, this formula is modified
already at
the leading order
PT, this formula is modified
already at
the leading order 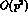 :
:  can be considerably
smaller than
can be considerably
smaller than 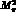 by an amount which depends on r. For r decreasing
from
by an amount which depends on r. For r decreasing
from  =25.9 to r=6.3,
=25.9 to r=6.3,  decreases from
decreases from 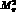 to zero. The low energy
to zero. The low energy  scattering thus provides us with a
quasi-unique experimental access to the order parameter
scattering thus provides us with a
quasi-unique experimental access to the order parameter 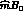 . The
corresponding G
. The
corresponding G PT predictions, endowed with the necessary loop
corrections, are presented in detail in the section on
PT predictions, endowed with the necessary loop
corrections, are presented in detail in the section on  interactions of
the present Handbook.
interactions of
the present Handbook.
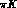 scattering [
scattering [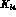 form factor R, which is measurable in the
form factor R, which is measurable in the
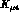 decay mode. Whereas the leading order predictions for the
decay mode. Whereas the leading order predictions for the 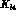 form factors F, G and H are identical in both schemes, there is a
detectable difference in the leading order expression for R [
form factors F, G and H are identical in both schemes, there is a
detectable difference in the leading order expression for R [