


Next: 6 Experimental tests
Up: Chapter 4 Section 3
Previous: 4 Examples of differences
It is not incorrect to state that G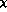 PT is more general just because it
admits a considerably wider range of values of certain low energy constants and
of the current quark masses than the standard scheme. On the other hand, the
standard
PT is more general just because it
admits a considerably wider range of values of certain low energy constants and
of the current quark masses than the standard scheme. On the other hand, the
standard  PT claims that the values of the
PT claims that the values of the 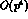 constants
constants  ,...,
,...,
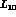 are well under control, both determinig them from data [2]
and estimating
them via resonance saturation [20,21]. Similar claims are
often made about the
values of the light quark masses [22]. The standard values of the low
energy parameters can indeed be justified within the set of assumptions
underlying the standard
are well under control, both determinig them from data [2]
and estimating
them via resonance saturation [20,21]. Similar claims are
often made about the
values of the light quark masses [22]. The standard values of the low
energy parameters can indeed be justified within the set of assumptions
underlying the standard  PT. However, beyond this framework, the same
experimental data, the same sum rules, etc..., can often yield rather different
results. We start by discussing the constants
PT. However, beyond this framework, the same
experimental data, the same sum rules, etc..., can often yield rather different
results. We start by discussing the constants 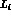 from the point of view of
G
from the point of view of
G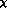 PT.
PT.
5a -  and
and 
These two constants appear in  , which is the part
common to both
, which is the part
common to both  and
and  . Their measurements
via the electromagnetic radius of the pion and the radiative decay
. Their measurements
via the electromagnetic radius of the pion and the radiative decay  [2] should not be altered
in G
[2] should not be altered
in G PT. Furthermore,
PT. Furthermore,  and
and 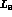 are, respectively, related to two and three point functions of vector and axial
vector currents dominated by vector and axial vector meson poles
[21,23]. This makes
the estimates of
are, respectively, related to two and three point functions of vector and axial
vector currents dominated by vector and axial vector meson poles
[21,23]. This makes
the estimates of 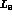 and of
and of 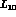 rather stable.
rather stable.
5b - 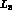 ,
, 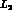 and
and 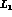
These remaining three constants of  are more difficult to
measure. Although they are not directly related to explicit symmetry breaking
effects, they enter the observables (
are more difficult to
measure. Although they are not directly related to explicit symmetry breaking
effects, they enter the observables (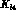 form factors [24],
form factors [24], 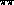 D-waves [2]) together with r-dependent loop corrections. Consequently,
for lower values of r, the standard determination of
D-waves [2]) together with r-dependent loop corrections. Consequently,
for lower values of r, the standard determination of  ,
, 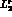 and
and
 is slightly modified [25], by not more than a factor of two.
is slightly modified [25], by not more than a factor of two.
The estimates of these constants via resonance saturation is also more involved
since, in addition to vector and axial vector mesons, 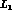 ,
,  and
and  receive a contribution from scalar exchanges, which are not known so well
[20]. The
reason of this complication is the fact that, unlike
receive a contribution from scalar exchanges, which are not known so well
[20]. The
reason of this complication is the fact that, unlike  and
and  ,
,  ,
,
 and
and 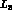 are related to four point functions of the vector and axial
currents.
are related to four point functions of the vector and axial
currents.
5c - 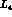 and
and 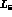
Let us concentrate on the 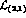 constant
constant 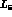 (
( violates the
Zweig rule) and, for simplicity, let us stick to the leading large
violates the
Zweig rule) and, for simplicity, let us stick to the leading large  behaviour, denoting the leading part of
behaviour, denoting the leading part of  by
by 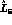 . One has (Eq.
(32)),
. One has (Eq.
(32)),
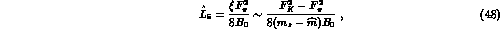
where we have used (30). The standard determination of 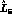 [2]
(or, equivalently, of
[2]
(or, equivalently, of 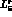 including
the chiral logarithms) would replace
including
the chiral logarithms) would replace 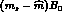 by
by 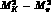 , leading to the value
, leading to the value 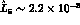 . Within G
. Within G PT, this last step could be misleading,
provided r is well below
PT, this last step could be misleading,
provided r is well below 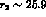 . Using instead the leading order
formula (26a) and neglecting the Zweig rule violating parameter
. Using instead the leading order
formula (26a) and neglecting the Zweig rule violating parameter 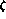 , one
obtains
, one
obtains
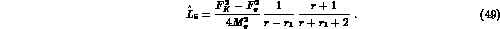
Hence, the value of 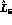 one extracts from Eq. (48) crucially depends
on the quark mass ratio r: For
one extracts from Eq. (48) crucially depends
on the quark mass ratio r: For 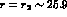 one gets the ``standard
value''
one gets the ``standard
value'' 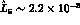 , whereas for r decreasing down to
, whereas for r decreasing down to
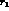 ,
, 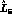 increases up to infinity. The estimates of
increases up to infinity. The estimates of  via
resonances merely concern scalar exchanges, whose description is considerably
more ambiguous [26] than in the case of vector and axial vector mesons
[21].
via
resonances merely concern scalar exchanges, whose description is considerably
more ambiguous [26] than in the case of vector and axial vector mesons
[21].
5d - 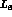 ,
, 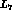 and
and 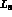
The values of these  constants are at the heart of our
discussion of symmetry breaking effects.
constants are at the heart of our
discussion of symmetry breaking effects.  violates the Zweig rule in the
violates the Zweig rule in the
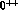 channel and it will not be discussed here. The combination
channel and it will not be discussed here. The combination  can be related to the deviation
can be related to the deviation  from the
Gell-Mann--Okubo mass formula [2] (see Eqs. (10) and (32)). The standard
evaluation of
from the
Gell-Mann--Okubo mass formula [2] (see Eqs. (10) and (32)). The standard
evaluation of 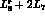 based on this relation suffers from a similar bias
as in the case of
based on this relation suffers from a similar bias
as in the case of 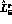 : The expression for
: The expression for 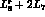 involves the
factor
involves the
factor 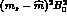 in the denominator. As a result, the value
of
in the denominator. As a result, the value
of 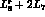 is even more sensitive to r than
is even more sensitive to r than 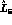 , and it can
actually be considerably larger than the standard value [2]
, and it can
actually be considerably larger than the standard value [2] 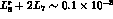 . A separate measurement of
. A separate measurement of 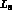 is usually based on
the relation with the isospin breaking quark mass ratio R (34), which is
known from different sources [2,9,14]. In G
is usually based on
the relation with the isospin breaking quark mass ratio R (34), which is
known from different sources [2,9,14]. In G PT, the relation
between
PT, the relation
between 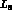 and R
can easily break down, for the same reason which could invalidate the
elliptic relation
(36): The importance of unduly neglected
and R
can easily break down, for the same reason which could invalidate the
elliptic relation
(36): The importance of unduly neglected 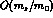 contributions. As a
consequence, the standard value [2] of
contributions. As a
consequence, the standard value [2] of 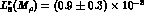 can be underestimated by as much as two orders of magnitude. Writing
can be underestimated by as much as two orders of magnitude. Writing
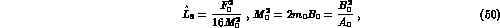
the renormalization group invariant mass parameter  can be estimated from
Eqs. (26a,b). In the standard scheme (
can be estimated from
Eqs. (26a,b). In the standard scheme (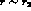 ),
),  is expected to be at a
GeV scale, whereas in G
is expected to be at a
GeV scale, whereas in G PT,
PT,  can be as small as
can be as small as  , or even
smaller.
, or even
smaller.
The estimate of  from resonance contributions can be obtained from
the two point function (3) which satisfies the superconvergent sum rule
[26]
from resonance contributions can be obtained from
the two point function (3) which satisfies the superconvergent sum rule
[26]
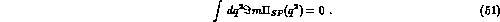
Saturating this sum rule by nothing but the pion and a single 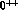 state of
mass
state of
mass  ,
one obtains
,
one obtains  GeV, leading to a value for
GeV, leading to a value for 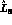 which is
of the standard order of magnitude
which is
of the standard order of magnitude 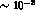 . Unfortunately, the above
argument does not by itself support the standard picture, and can be
turned around: If
. Unfortunately, the above
argument does not by itself support the standard picture, and can be
turned around: If
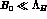 , the pion contribution (
, the pion contribution (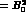 ) can hardly dominate the
pseudoscalar component of the sum rule (51). In order to balance the scalar
contribution, one has to include an excited
) can hardly dominate the
pseudoscalar component of the sum rule (51). In order to balance the scalar
contribution, one has to include an excited  state of mass
state of mass
 ,
,  MeV. It is then easy to see that the mass
parameter
MeV. It is then easy to see that the mass
parameter  in Eq. (50) can take any value between zero and
in Eq. (50) can take any value between zero and 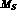 [26].
[26].
Quite generally, the introduction of J=0 resonances, compatible with chiral
symmetry and with the short distance properties of QCD correlation functions,
into the effective
lagrangian [20] is more tricky and more ambiguous
than in the case of J=1 states [21]. The authors of Ref. [20]
have, for
instance, decided to disregard the contribution of the  nonet.
Doing so, they have a priori eliminated the low
nonet.
Doing so, they have a priori eliminated the low 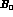 alternative.
alternative.
The standard 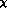 PT rewrites the expansion in quark masses as an expansion in
powers of
PT rewrites the expansion in quark masses as an expansion in
powers of 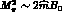 . In the vicinity of the
antiferromagnetic critical point,
. In the vicinity of the
antiferromagnetic critical point, 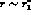 , the coefficients of the latter
expansion, viz.
, the coefficients of the latter
expansion, viz. 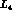 ...
...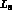 , blow up, and the expansion has to be redefined.
G
, blow up, and the expansion has to be redefined.
G PT is precisely such a redefinition. At the leading order, it is
characterized by a single undetermined parameter not present in the standard
scheme, the quark mass ratio
PT is precisely such a redefinition. At the leading order, it is
characterized by a single undetermined parameter not present in the standard
scheme, the quark mass ratio 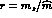 . One may say that G
. One may say that G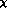 PT
parametrizes the deviations from standard predictions of
PT
parametrizes the deviations from standard predictions of 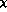 PT in terms of
the deviation of r from its standard value
PT in terms of
the deviation of r from its standard value  [2].
[2].
5e - Running light quark masses
In G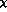 PT, the decrease of the quark mass ratio r from
PT, the decrease of the quark mass ratio r from 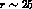 to
to
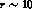 is likely to be interpreted as an increase in the value of the
running quark mass
is likely to be interpreted as an increase in the value of the
running quark mass 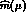 by a factor of
by a factor of  . The order of
magnitude of the mass differences
. The order of
magnitude of the mass differences  and
and  should
remain essentially unchanged. In this connection, it should be stressed that
all existing estimates of
should
remain essentially unchanged. In this connection, it should be stressed that
all existing estimates of 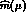 use in one way or the other the
assumption
use in one way or the other the
assumption  . This is obvious for those approaches which deduce the
value of
. This is obvious for those approaches which deduce the
value of  from the estimates of
from the estimates of 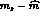 [8,9]. It is however even true in the case of direct quantitative
determinations of
[8,9]. It is however even true in the case of direct quantitative
determinations of 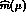 from QCD sum rules [17]. The latter
express the square of
from QCD sum rules [17]. The latter
express the square of 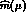 as a weighted integral of the
spectral function (43). Nothing is known experimentally about
as a weighted integral of the
spectral function (43). Nothing is known experimentally about  beyond the one pion intermediate state contribution. The only existing attempt
to fill this gap makes use of the low
beyond the one pion intermediate state contribution. The only existing attempt
to fill this gap makes use of the low 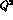 behaviour (44) of
behaviour (44) of
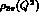 as given by the
standard
as given by the
standard  PT in order to normalize the whole
PT in order to normalize the whole  contribution
represented by a broad
contribution
represented by a broad  Breit-Wigner peak. In this way, the
result
Breit-Wigner peak. In this way, the
result 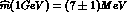 is obtained [17].
If, instead,
the
is obtained [17].
If, instead,
the  contribution is normalized using the G
contribution is normalized using the G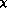 PT result (45), the
above value of
PT result (45), the
above value of 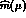 is increased by a factor
is increased by a factor 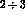 . (Let us
note in passing that within G
. (Let us
note in passing that within G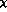 PT, the possibility of having
PT, the possibility of having 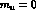 appears even less likely than in the standard case [14].)
appears even less likely than in the standard case [14].)
In general, G PT admits and expects a larger absolute strength of the
divergence of the
PT admits and expects a larger absolute strength of the
divergence of the 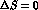 axial current away from the pion pole than the
standard scheme could possibly tolerate. The physical origin of this increase
would be ascribed to the importance of the ``
axial current away from the pion pole than the
standard scheme could possibly tolerate. The physical origin of this increase
would be ascribed to the importance of the `` contribution'',
which can and should be checked experimentally: The
contribution'',
which can and should be checked experimentally: The  component of the spectral function (43) can be measured in high statistics
component of the spectral function (43) can be measured in high statistics
 decay experiments [18], and in this way, the
determination of
decay experiments [18], and in this way, the
determination of  could be put on a solid experimental
basis.
could be put on a solid experimental
basis.
Concluding this section, it is worth emphasizing that nothing in the preceeding
discussion indicates that the standard determination of the 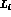 's and of the
light quark masses is internally inconsistent. The standard
's and of the
light quark masses is internally inconsistent. The standard  PT together
with the standard value of the low energy parameters is a perfectly
self-consistent scheme. However, it is not the only possible consistent
scheme and it does not contain its proper justification.
PT together
with the standard value of the low energy parameters is a perfectly
self-consistent scheme. However, it is not the only possible consistent
scheme and it does not contain its proper justification.



Next: 6 Experimental tests
Up: Chapter 4 Section 3
Previous: 4 Examples of differences
Carlos E.Piedrafita
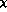 PT is more general just because it
admits a considerably wider range of values of certain low energy constants and
of the current quark masses than the standard scheme. On the other hand, the
standard
PT is more general just because it
admits a considerably wider range of values of certain low energy constants and
of the current quark masses than the standard scheme. On the other hand, the
standard  PT claims that the values of the
PT claims that the values of the 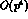 constants
constants  ,...,
,...,
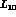 are well under control, both determinig them from data [2]
and estimating
them via resonance saturation [20,21]. Similar claims are
often made about the
values of the light quark masses [22]. The standard values of the low
energy parameters can indeed be justified within the set of assumptions
underlying the standard
are well under control, both determinig them from data [2]
and estimating
them via resonance saturation [20,21]. Similar claims are
often made about the
values of the light quark masses [22]. The standard values of the low
energy parameters can indeed be justified within the set of assumptions
underlying the standard  PT. However, beyond this framework, the same
experimental data, the same sum rules, etc..., can often yield rather different
results. We start by discussing the constants
PT. However, beyond this framework, the same
experimental data, the same sum rules, etc..., can often yield rather different
results. We start by discussing the constants 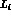 from the point of view of
G
from the point of view of
G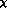 PT.
PT.
 and
and 
 , which is the part
common to both
, which is the part
common to both  and
and  . Their measurements
via the electromagnetic radius of the pion and the radiative decay
. Their measurements
via the electromagnetic radius of the pion and the radiative decay  [
[ PT. Furthermore,
PT. Furthermore,  and
and 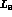 are, respectively, related to two and three point functions of vector and axial
vector currents dominated by vector and axial vector meson poles
[
are, respectively, related to two and three point functions of vector and axial
vector currents dominated by vector and axial vector meson poles
[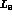 and of
and of 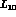 rather stable.
rather stable.
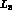 ,
, 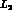 and
and 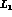
 are more difficult to
measure. Although they are not directly related to explicit symmetry breaking
effects, they enter the observables (
are more difficult to
measure. Although they are not directly related to explicit symmetry breaking
effects, they enter the observables (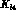 form factors [
form factors [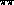 D-waves [
D-waves [ ,
, 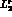 and
and
 is slightly modified [
is slightly modified [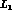 ,
,  and
and  receive a contribution from scalar exchanges, which are not known so well
[
receive a contribution from scalar exchanges, which are not known so well
[ and
and  ,
,  ,
,
 and
and 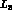 are related to four point functions of the vector and axial
currents.
are related to four point functions of the vector and axial
currents.
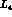 and
and 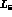
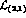 constant
constant 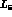 (
( violates the
Zweig rule) and, for simplicity, let us stick to the leading large
violates the
Zweig rule) and, for simplicity, let us stick to the leading large  behaviour, denoting the leading part of
behaviour, denoting the leading part of  by
by 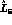 . One has (Eq.
(32)),
. One has (Eq.
(32)),
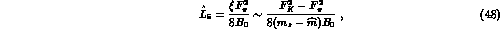
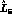 [
[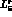 including
the chiral logarithms) would replace
including
the chiral logarithms) would replace 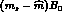 by
by 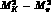 , leading to the value
, leading to the value 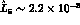 . Within G
. Within G PT, this last step could be misleading,
provided r is well below
PT, this last step could be misleading,
provided r is well below 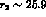 . Using instead the leading order
formula (26a) and neglecting the Zweig rule violating parameter
. Using instead the leading order
formula (26a) and neglecting the Zweig rule violating parameter 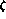 , one
obtains
, one
obtains
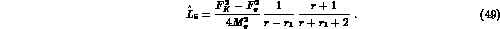
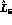 one extracts from Eq. (48) crucially depends
on the quark mass ratio r: For
one extracts from Eq. (48) crucially depends
on the quark mass ratio r: For 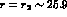 one gets the ``standard
value''
one gets the ``standard
value'' 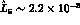 , whereas for r decreasing down to
, whereas for r decreasing down to
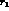 ,
, 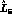 increases up to infinity. The estimates of
increases up to infinity. The estimates of  via
resonances merely concern scalar exchanges, whose description is considerably
more ambiguous [
via
resonances merely concern scalar exchanges, whose description is considerably
more ambiguous [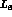 ,
, 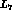 and
and 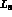
 constants are at the heart of our
discussion of symmetry breaking effects.
constants are at the heart of our
discussion of symmetry breaking effects.  violates the Zweig rule in the
violates the Zweig rule in the
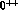 channel and it will not be discussed here. The combination
channel and it will not be discussed here. The combination  can be related to the deviation
can be related to the deviation  from the
Gell-Mann--Okubo mass formula [
from the
Gell-Mann--Okubo mass formula [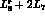 based on this relation suffers from a similar bias
as in the case of
based on this relation suffers from a similar bias
as in the case of 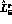 : The expression for
: The expression for 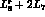 involves the
factor
involves the
factor 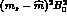 in the denominator. As a result, the value
of
in the denominator. As a result, the value
of 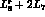 is even more sensitive to r than
is even more sensitive to r than 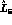 , and it can
actually be considerably larger than the standard value [
, and it can
actually be considerably larger than the standard value [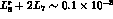 . A separate measurement of
. A separate measurement of 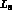 is usually based on
the relation with the isospin breaking quark mass ratio R (34), which is
known from different sources [
is usually based on
the relation with the isospin breaking quark mass ratio R (34), which is
known from different sources [ PT, the relation
between
PT, the relation
between 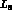 and R
can easily break down, for the same reason which could invalidate the
elliptic relation
(36): The importance of unduly neglected
and R
can easily break down, for the same reason which could invalidate the
elliptic relation
(36): The importance of unduly neglected 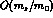 contributions. As a
consequence, the standard value [
contributions. As a
consequence, the standard value [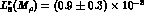 can be underestimated by as much as two orders of magnitude. Writing
can be underestimated by as much as two orders of magnitude. Writing
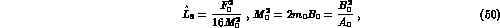
 can be estimated from
Eqs. (26a,b). In the standard scheme (
can be estimated from
Eqs. (26a,b). In the standard scheme ( ),
),  is expected to be at a
GeV scale, whereas in G
is expected to be at a
GeV scale, whereas in G PT,
PT,  can be as small as
can be as small as  , or even
smaller.
, or even
smaller.
 from resonance contributions can be obtained from
the two point function (3) which satisfies the superconvergent sum rule
[
from resonance contributions can be obtained from
the two point function (3) which satisfies the superconvergent sum rule
[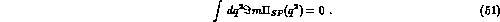
 state of
mass
state of
mass  ,
one obtains
,
one obtains  GeV, leading to a value for
GeV, leading to a value for 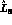 which is
of the standard order of magnitude
which is
of the standard order of magnitude 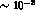 . Unfortunately, the above
argument does not by itself support the standard picture, and can be
turned around: If
. Unfortunately, the above
argument does not by itself support the standard picture, and can be
turned around: If
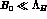 , the pion contribution (
, the pion contribution (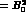 ) can hardly dominate the
pseudoscalar component of the sum rule (51). In order to balance the scalar
contribution, one has to include an excited
) can hardly dominate the
pseudoscalar component of the sum rule (51). In order to balance the scalar
contribution, one has to include an excited  state of mass
state of mass
 ,
,  MeV. It is then easy to see that the mass
parameter
MeV. It is then easy to see that the mass
parameter  in Eq. (50) can take any value between zero and
in Eq. (50) can take any value between zero and 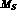 [
[ nonet.
Doing so, they have a priori eliminated the low
nonet.
Doing so, they have a priori eliminated the low 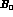 alternative.
alternative.
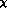 PT rewrites the expansion in quark masses as an expansion in
powers of
PT rewrites the expansion in quark masses as an expansion in
powers of 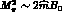 . In the vicinity of the
antiferromagnetic critical point,
. In the vicinity of the
antiferromagnetic critical point, 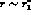 , the coefficients of the latter
expansion, viz.
, the coefficients of the latter
expansion, viz. 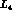 ...
...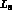 , blow up, and the expansion has to be redefined.
G
, blow up, and the expansion has to be redefined.
G PT is precisely such a redefinition. At the leading order, it is
characterized by a single undetermined parameter not present in the standard
scheme, the quark mass ratio
PT is precisely such a redefinition. At the leading order, it is
characterized by a single undetermined parameter not present in the standard
scheme, the quark mass ratio 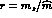 . One may say that G
. One may say that G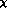 PT
parametrizes the deviations from standard predictions of
PT
parametrizes the deviations from standard predictions of 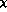 PT in terms of
the deviation of r from its standard value
PT in terms of
the deviation of r from its standard value  [
[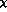 PT, the decrease of the quark mass ratio r from
PT, the decrease of the quark mass ratio r from 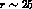 to
to
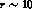 is likely to be interpreted as an increase in the value of the
running quark mass
is likely to be interpreted as an increase in the value of the
running quark mass 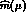 by a factor of
by a factor of  . The order of
magnitude of the mass differences
. The order of
magnitude of the mass differences  and
and  should
remain essentially unchanged. In this connection, it should be stressed that
all existing estimates of
should
remain essentially unchanged. In this connection, it should be stressed that
all existing estimates of 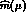 use in one way or the other the
assumption
use in one way or the other the
assumption  . This is obvious for those approaches which deduce the
value of
. This is obvious for those approaches which deduce the
value of  from the estimates of
from the estimates of 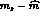 [
[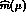 from QCD sum rules [
from QCD sum rules [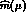 as a weighted integral of the
spectral function (43). Nothing is known experimentally about
as a weighted integral of the
spectral function (43). Nothing is known experimentally about  beyond the one pion intermediate state contribution. The only existing attempt
to fill this gap makes use of the low
beyond the one pion intermediate state contribution. The only existing attempt
to fill this gap makes use of the low 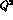 behaviour (44) of
behaviour (44) of
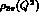 as given by the
standard
as given by the
standard  PT in order to normalize the whole
PT in order to normalize the whole  contribution
represented by a broad
contribution
represented by a broad  Breit-Wigner peak. In this way, the
result
Breit-Wigner peak. In this way, the
result 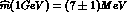 is obtained [
is obtained [ contribution is normalized using the G
contribution is normalized using the G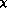 PT result (45), the
above value of
PT result (45), the
above value of 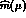 is increased by a factor
is increased by a factor 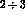 . (Let us
note in passing that within G
. (Let us
note in passing that within G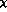 PT, the possibility of having
PT, the possibility of having 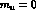 appears even less likely than in the standard case [
appears even less likely than in the standard case [ PT admits and expects a larger absolute strength of the
divergence of the
PT admits and expects a larger absolute strength of the
divergence of the 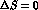 axial current away from the pion pole than the
standard scheme could possibly tolerate. The physical origin of this increase
would be ascribed to the importance of the ``
axial current away from the pion pole than the
standard scheme could possibly tolerate. The physical origin of this increase
would be ascribed to the importance of the `` contribution'',
which can and should be checked experimentally: The
contribution'',
which can and should be checked experimentally: The  component of the spectral function (43) can be measured in high statistics
component of the spectral function (43) can be measured in high statistics
 decay experiments [
decay experiments [ could be put on a solid experimental
basis.
could be put on a solid experimental
basis.
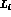 's and of the
light quark masses is internally inconsistent. The standard
's and of the
light quark masses is internally inconsistent. The standard  PT together
with the standard value of the low energy parameters is a perfectly
self-consistent scheme. However, it is not the only possible consistent
scheme and it does not contain its proper justification.
PT together
with the standard value of the low energy parameters is a perfectly
self-consistent scheme. However, it is not the only possible consistent
scheme and it does not contain its proper justification.