


Next: 4 Examples of differences
Up: Chapter 4 Section 3
Previous: 2 Expansion of Goldstone
The above remarks do not affect the construction of the low energy effective
Lagrangian [10]. Its form is merely dictated by the chiral symmetry
[11] and
by the transformation properties of the symmetry breaking quark mass term, and
there is obviously no question to alter these fundamental properties of QCD.
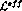 is a function of 8 Goldstone boson fields
(conventionally collected into an SU(3) element U) and of external sources
is a function of 8 Goldstone boson fields
(conventionally collected into an SU(3) element U) and of external sources
 and p, the scalar source
s containing the quark mass matrix
and p, the scalar source
s containing the quark mass matrix 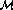 .
The formalism and notation used here are standard [2], unless
otherwise stated.
.
The formalism and notation used here are standard [2], unless
otherwise stated. 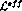 consists of an infinite tower of
invariants
consists of an infinite tower of
invariants
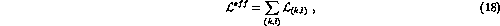
where  contains k powers of covariant derivatives and
l powers of
scalar or pseudoscalar sources. In the low energy limit,
contains k powers of covariant derivatives and
l powers of
scalar or pseudoscalar sources. In the low energy limit,  vanishes
like the k-th power of external momenta p and the l-th power of
the quark mass
vanishes
like the k-th power of external momenta p and the l-th power of
the quark mass  ,
,
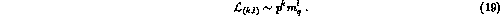
Chiral perturbation theory
is an expansion of 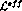 in powers of the pion (kaon)
mass assuming that all external momenta are of that size. For sufficiently
small quark masses,
such that both
in powers of the pion (kaon)
mass assuming that all external momenta are of that size. For sufficiently
small quark masses,
such that both 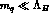 and
and 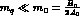 hold,
one has
hold,
one has
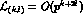 . In this case, one can write
. In this case, one can write

where [2]
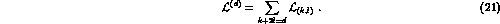
This expansion defines the standard  PT. If, on the other hand, for actual
values of quark masses one has
PT. If, on the other hand, for actual
values of quark masses one has 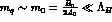 , both
, both
 and
and 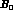 should count as parameters of the size of the pion mass and,
consequently,
should count as parameters of the size of the pion mass and,
consequently, 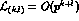 . This new counting yields
a different
expansion of
. This new counting yields
a different
expansion of 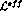 ,
,

where [4]
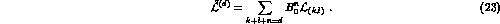
It should be stressed that Eqs. (20) and (22) represent
two different expansions
of the same effective Lagrangian.
To all orders they are identical, at a given
finite order they may differ.
It is straightforward to write down the most general expression [4] of
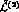 which defines the leading
which defines the leading 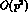 order of G
order of G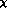 PT :
PT :
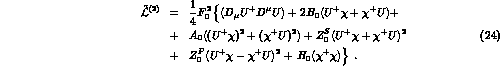
Here 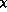 collects the scalar and pseudoscalar sources,
collects the scalar and pseudoscalar sources,
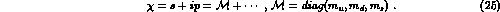
Notice the absence of the factor 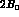 , which appears in the standard
definition of
, which appears in the standard
definition of 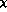 [2]. The meaning
of this difference will shortly become
obvious. Compared to
[2]. The meaning
of this difference will shortly become
obvious. Compared to  , Eq. (24) contains
additional terms. The
constants
, Eq. (24) contains
additional terms. The
constants 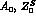 and
and  are the same as introduced in the previous
section : Eq. (5), (with
are the same as introduced in the previous
section : Eq. (5), (with 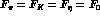 and
and 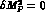 )
is indeed a
straightforward consequence of the Lagrangian (24).
The fact that the
)
is indeed a
straightforward consequence of the Lagrangian (24).
The fact that the  and
and 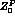 terms now appear at the same order
terms now appear at the same order 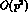 as the
as the 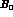 term
reflects the possibility that in Eqs. (5) the first order and second order terms
are of comparable size. To this order
term
reflects the possibility that in Eqs. (5) the first order and second order terms
are of comparable size. To this order 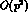 , the low energy constants in
(24)
can be expressed in terms of physical masses
, the low energy constants in
(24)
can be expressed in terms of physical masses 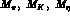 , of
the quark mass
ratio
, of
the quark mass
ratio 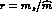 and of the Zweig rule violating parameter
and of the Zweig rule violating parameter  (14).
Expanding Eqs. (12a), (12b) and (10), one gets
(14).
Expanding Eqs. (12a), (12b) and (10), one gets

where 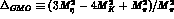 . It is seen
that for the
particular values of the parameters
. It is seen
that for the
particular values of the parameters 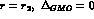 , Eqs. (26) imply
, Eqs. (26) imply
 and
and 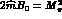 , i.e. one recovers the standard
, i.e. one recovers the standard
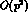 Lagrangian
Lagrangian 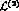 . Order by order, G
. Order by order, G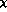 PT contains the
standard
PT contains the
standard 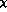 PT as a special case.
PT as a special case.
The next to the leading term of the expansion (22) is
of odd order 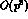 , which is a new
feature, absent in the standard
, which is a new
feature, absent in the standard  PT. One has [6]
PT. One has [6]
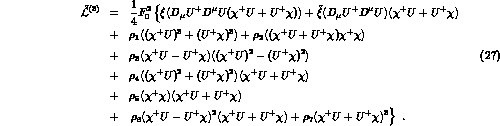
In writing down Eq. (27), we have adopted some
conventions which are worth to be
specified. The parameters of 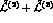 are
finite, (divergences only start at order
are
finite, (divergences only start at order  ) and they may be viewed as
independent variables. It is convenient to tag each of these variables by a
QCD correlation function. An example is the
) and they may be viewed as
independent variables. It is convenient to tag each of these variables by a
QCD correlation function. An example is the  parameter
parameter  , closely
related to the two-point function (3). This relation
may be further specified as
, closely
related to the two-point function (3). This relation
may be further specified as
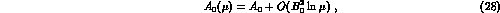
where 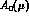 is defined by Eq. (4). Here, the statement
is that the
expansion of
is defined by Eq. (4). Here, the statement
is that the
expansion of 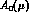 in powers of
in powers of 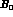 does not contain a linear term. This
constrains the way one writes
does not contain a linear term. This
constrains the way one writes  :
:
i) A term 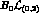 which, according to Eq. (23) could be
present in
which, according to Eq. (23) could be
present in 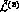 , is obviously irrelevant. It can be absorbed
into the covariant transformation of sources
, is obviously irrelevant. It can be absorbed
into the covariant transformation of sources 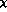 and of parameters of
and of parameters of 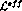 which has been discovered some times ago by Kaplan and Manohar
[12],
(see also Ref. [13]). Indeed, Eq. (28) may be
viewed as a physical condition
fixing the reparametrization ambiguity of
which has been discovered some times ago by Kaplan and Manohar
[12],
(see also Ref. [13]). Indeed, Eq. (28) may be
viewed as a physical condition
fixing the reparametrization ambiguity of  pointed out in
[12] and in [13]. In general, the
pointed out in
[12] and in [13]. In general, the  dependent terms in Eq. (23)
will be
introduced only if they are required by renormalization. This is not the case
of
dependent terms in Eq. (23)
will be
introduced only if they are required by renormalization. This is not the case
of 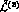 .
.
ii) Similarly, a 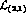 term like
term like
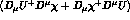 which would yield a contribution to Eq. (28) linear in
which would yield a contribution to Eq. (28) linear in  , can be
transformed away by a source dependent redefinition of Goldstone boson fields.
Notice that this convention has not been used in Ref. [4].
, can be
transformed away by a source dependent redefinition of Goldstone boson fields.
Notice that this convention has not been used in Ref. [4].
The main physical effect described by the Lagrangian 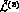 is the splitting of the decay constants
is the splitting of the decay constants  , and
, and 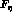 .
One easily finds
.
One easily finds
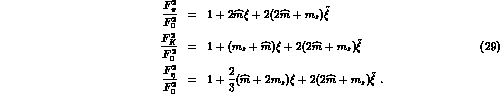
This allows to express the constant  as
as
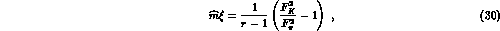
whereas the Zweig rule violating parameter 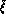 remains at this stage
undetermined. The
remains at this stage
undetermined. The  part of
part of  ,
described by
the constants
,
described by
the constants  generates an
generates an 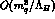 contribution
to the pseudoscalar masses. Notice that in the standard
contribution
to the pseudoscalar masses. Notice that in the standard  PT these terms
would count as
PT these terms
would count as 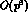 .
.
 provides the simplest example of odd chiral orders
characteristic of G
provides the simplest example of odd chiral orders
characteristic of G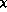 PT. They do not correspond to an increase in the
number of loops, but to additional corrections in powers of the quark masses. In
the standard
PT. They do not correspond to an increase in the
number of loops, but to additional corrections in powers of the quark masses. In
the standard 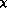 PT [2], the splitting in
the decay constants is a
PT [2], the splitting in
the decay constants is a 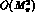 effect arising from loops (tadpoles) and from the corresponding counterterms
contained in
effect arising from loops (tadpoles) and from the corresponding counterterms
contained in 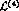 . Here, the leading contribution (30) counts
as
. Here, the leading contribution (30) counts
as 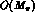 , (actually, it can hardly be expressed in terms of the pion
mass), and the loop effects only show up at the next,
, (actually, it can hardly be expressed in terms of the pion
mass), and the loop effects only show up at the next, 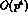 , order. Notice
that for
, order. Notice
that for 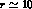 , the constant (30) is of the order
, the constant (30) is of the order
 - a typical size of other
- a typical size of other  effects, such as the deviation from
the Goldberger-Treiman relation.
effects, such as the deviation from
the Goldberger-Treiman relation.
The Lagrangian 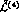 describing the next order,
describing the next order, 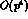 ,
consists of several components :
,
consists of several components :
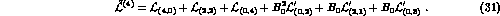
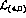 is the part of the standard
is the part of the standard 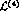 , which
consists of four derivatives and contains no
, which
consists of four derivatives and contains no  , i.e. no quark mass :
, i.e. no quark mass :
 is given by the standard five terms [2]
described by the low energy
constants
is given by the standard five terms [2]
described by the low energy
constants 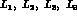 and
and 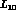 .
. 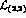 is a new term,
which in the standard
is a new term,
which in the standard 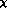 PT would count as
PT would count as  , whereas
, whereas
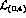 involves 4 insertions of a quark mass, and in the standard
involves 4 insertions of a quark mass, and in the standard
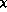 PT it would be relegated up to the order
PT it would be relegated up to the order  .
.  and
and
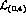 involve about 20 independent terms each. An experimental
determination of all the corresponding low energy constants is obviously hard
to imagine. However, a few particular combinations of these constants which
contribute, for instance, to
involve about 20 independent terms each. An experimental
determination of all the corresponding low energy constants is obviously hard
to imagine. However, a few particular combinations of these constants which
contribute, for instance, to  and
and 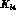 decays, or to the
decays, or to the  scattering amplitude at the one loop level, can be estimated and included into
the analysis.
scattering amplitude at the one loop level, can be estimated and included into
the analysis.
The last three terms in Eq. (31) represent  -dependent
counterterms of order
-dependent
counterterms of order
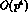 which are needed to renormalize one loop divergences that arise from
using the vertices of
which are needed to renormalize one loop divergences that arise from
using the vertices of 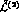 alone in the loop. They renormalize
the constants
alone in the loop. They renormalize
the constants 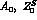 by higher order contributions, of order
by higher order contributions, of order 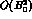 ,
and the constants
,
and the constants 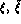 and
and 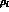 by an amount
by an amount  . In
generalized
. In
generalized 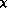 PT, renormalization proceeds order by order in the expansion
in powers of the constant
PT, renormalization proceeds order by order in the expansion
in powers of the constant 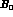 .
.
The standard 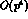 order Lagrangian
order Lagrangian 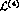 contains 10
low energy constants
contains 10
low energy constants 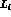 [2]. They are all involved in
[2]. They are all involved in
 . As already
pointed out,
. As already
pointed out, 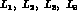 and
and 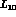 - the constants of
- the constants of
 - play an identical role in both schemes.
- play an identical role in both schemes. 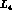 and
and 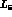 are
related to the constants
are
related to the constants 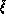 and
and 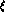 in
in  :
:
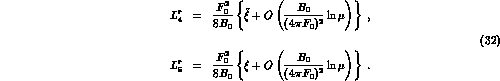
Finally, the standard  constants
constants 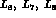 are related to the
are related to the
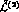 constants
constants 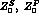 and
and  , respectively :
, respectively :
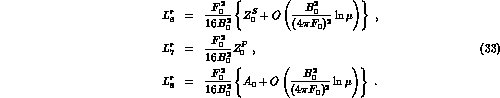
On the other hand, 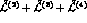 involves additional terms, not contained in
involves additional terms, not contained in 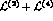 , and which the standard
, and which the standard  PT relegates to higher
orders d>4. Setting the corresponding additional constants to zero, one
recovers the standard
PT relegates to higher
orders d>4. Setting the corresponding additional constants to zero, one
recovers the standard 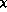 PT up to and including order
PT up to and including order 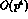 . This
phenomenon is general: Order by order, the standard expansion reappears as a
special case of G
. This
phenomenon is general: Order by order, the standard expansion reappears as a
special case of G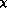 PT.
PT.



Next: 4 Examples of differences
Up: Chapter 4 Section 3
Previous: 2 Expansion of Goldstone
Carlos E.Piedrafita
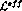 is a function of 8 Goldstone boson fields
(conventionally collected into an SU(3) element U) and of external sources
is a function of 8 Goldstone boson fields
(conventionally collected into an SU(3) element U) and of external sources
 and p, the scalar source
s containing the quark mass matrix
and p, the scalar source
s containing the quark mass matrix 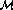 .
The formalism and notation used here are standard [2], unless
otherwise stated.
.
The formalism and notation used here are standard [2], unless
otherwise stated. 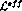 consists of an infinite tower of
invariants
consists of an infinite tower of
invariants
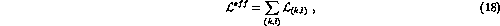
 contains k powers of covariant derivatives and
l powers of
scalar or pseudoscalar sources. In the low energy limit,
contains k powers of covariant derivatives and
l powers of
scalar or pseudoscalar sources. In the low energy limit,  vanishes
like the k-th power of external momenta p and the l-th power of
the quark mass
vanishes
like the k-th power of external momenta p and the l-th power of
the quark mass  ,
,
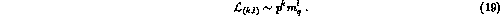
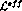 in powers of the pion (kaon)
mass assuming that all external momenta are of that size. For sufficiently
small quark masses,
such that both
in powers of the pion (kaon)
mass assuming that all external momenta are of that size. For sufficiently
small quark masses,
such that both 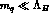 and
and 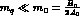 hold,
one has
hold,
one has
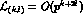 . In this case, one can write
. In this case, one can write

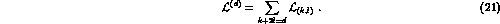
 PT. If, on the other hand, for actual
values of quark masses one has
PT. If, on the other hand, for actual
values of quark masses one has 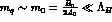 , both
, both
 and
and 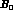 should count as parameters of the size of the pion mass and,
consequently,
should count as parameters of the size of the pion mass and,
consequently, 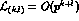 . This new counting yields
a different
expansion of
. This new counting yields
a different
expansion of 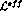 ,
,

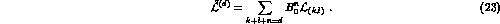
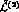 which defines the leading
which defines the leading 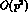 order of G
order of G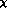 PT :
PT :
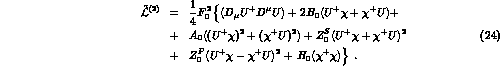
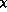 collects the scalar and pseudoscalar sources,
collects the scalar and pseudoscalar sources,
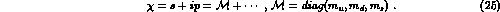
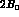 , which appears in the standard
definition of
, which appears in the standard
definition of 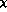 [
[ , Eq. (
, Eq. (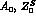 and
and  are the same as introduced in the previous
section : Eq. (5), (with
are the same as introduced in the previous
section : Eq. (5), (with 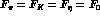 and
and 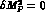 )
is indeed a
straightforward consequence of the Lagrangian (
)
is indeed a
straightforward consequence of the Lagrangian ( and
and 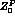 terms now appear at the same order
terms now appear at the same order 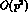 as the
as the 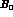 term
reflects the possibility that in Eqs. (5) the first order and second order terms
are of comparable size. To this order
term
reflects the possibility that in Eqs. (5) the first order and second order terms
are of comparable size. To this order 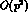 , the low energy constants in
(
, the low energy constants in
(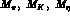 , of
the quark mass
ratio
, of
the quark mass
ratio 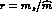 and of the Zweig rule violating parameter
and of the Zweig rule violating parameter  (
(
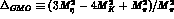 . It is seen
that for the
particular values of the parameters
. It is seen
that for the
particular values of the parameters 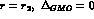 , Eqs. (26) imply
, Eqs. (26) imply
 and
and 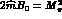 , i.e. one recovers the standard
, i.e. one recovers the standard
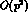 Lagrangian
Lagrangian 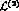 . Order by order, G
. Order by order, G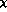 PT contains the
standard
PT contains the
standard 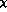 PT as a special case.
PT as a special case.
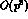 , which is a new
feature, absent in the standard
, which is a new
feature, absent in the standard  PT. One has [
PT. One has [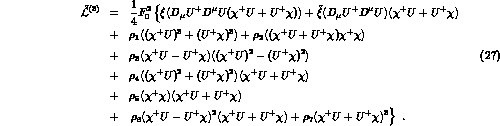
 are
finite, (divergences only start at order
are
finite, (divergences only start at order  ) and they may be viewed as
independent variables. It is convenient to tag each of these variables by a
QCD correlation function. An example is the
) and they may be viewed as
independent variables. It is convenient to tag each of these variables by a
QCD correlation function. An example is the  parameter
parameter  , closely
related to the two-point function (
, closely
related to the two-point function (
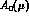 is defined by Eq. (
is defined by Eq. (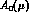 in powers of
in powers of 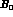 does not contain a linear term. This
constrains the way one writes
does not contain a linear term. This
constrains the way one writes  :
:
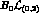 which, according to Eq. (
which, according to Eq. (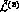 , is obviously irrelevant. It can be absorbed
into the covariant transformation of sources
, is obviously irrelevant. It can be absorbed
into the covariant transformation of sources 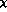 and of parameters of
and of parameters of 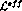 which has been discovered some times ago by Kaplan and Manohar
[
which has been discovered some times ago by Kaplan and Manohar
[ pointed out in
[
pointed out in
[ dependent terms in Eq. (
dependent terms in Eq. (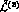 .
.
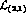 term like
term like
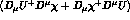 which would yield a contribution to Eq. (
which would yield a contribution to Eq. ( , can be
transformed away by a source dependent redefinition of Goldstone boson fields.
Notice that this convention has not been used in Ref. [
, can be
transformed away by a source dependent redefinition of Goldstone boson fields.
Notice that this convention has not been used in Ref. [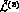 is the splitting of the decay constants
is the splitting of the decay constants  , and
, and 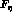 .
One easily finds
.
One easily finds
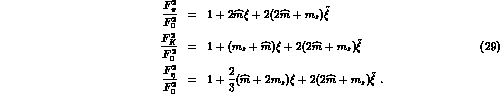
 as
as
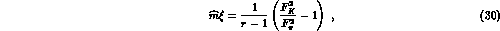
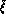 remains at this stage
undetermined. The
remains at this stage
undetermined. The 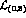 part of
part of 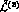 ,
described by
the constants
,
described by
the constants  generates an
generates an 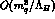 contribution
to the pseudoscalar masses. Notice that in the standard
contribution
to the pseudoscalar masses. Notice that in the standard  PT these terms
would count as
PT these terms
would count as 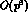 .
.
 provides the simplest example of odd chiral orders
characteristic of G
provides the simplest example of odd chiral orders
characteristic of G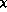 PT. They do not correspond to an increase in the
number of loops, but to additional corrections in powers of the quark masses. In
the standard
PT. They do not correspond to an increase in the
number of loops, but to additional corrections in powers of the quark masses. In
the standard 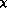 PT [
PT [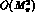 effect arising from loops (tadpoles) and from the corresponding counterterms
contained in
effect arising from loops (tadpoles) and from the corresponding counterterms
contained in 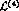 . Here, the leading contribution (
. Here, the leading contribution (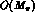 , (actually, it can hardly be expressed in terms of the pion
mass), and the loop effects only show up at the next,
, (actually, it can hardly be expressed in terms of the pion
mass), and the loop effects only show up at the next, 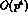 , order. Notice
that for
, order. Notice
that for 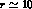 , the constant (
, the constant ( - a typical size of other
- a typical size of other  effects, such as the deviation from
the Goldberger-Treiman relation.
effects, such as the deviation from
the Goldberger-Treiman relation.
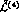 describing the next order,
describing the next order, 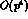 ,
consists of several components :
,
consists of several components :
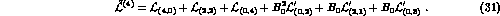
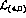 is the part of the standard
is the part of the standard 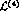 , which
consists of four derivatives and contains no
, which
consists of four derivatives and contains no  , i.e. no quark mass :
, i.e. no quark mass :
 is given by the standard five terms [
is given by the standard five terms [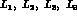 and
and 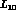 .
. 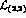 is a new term,
which in the standard
is a new term,
which in the standard 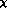 PT would count as
PT would count as  , whereas
, whereas
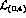 involves 4 insertions of a quark mass, and in the standard
involves 4 insertions of a quark mass, and in the standard
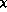 PT it would be relegated up to the order
PT it would be relegated up to the order  .
.  and
and
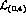 involve about 20 independent terms each. An experimental
determination of all the corresponding low energy constants is obviously hard
to imagine. However, a few particular combinations of these constants which
contribute, for instance, to
involve about 20 independent terms each. An experimental
determination of all the corresponding low energy constants is obviously hard
to imagine. However, a few particular combinations of these constants which
contribute, for instance, to  and
and 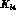 decays, or to the
decays, or to the  scattering amplitude at the one loop level, can be estimated and included into
the analysis.
scattering amplitude at the one loop level, can be estimated and included into
the analysis.
 -dependent
counterterms of order
-dependent
counterterms of order
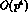 which are needed to renormalize one loop divergences that arise from
using the vertices of
which are needed to renormalize one loop divergences that arise from
using the vertices of 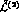 alone in the loop. They renormalize
the constants
alone in the loop. They renormalize
the constants 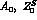 by higher order contributions, of order
by higher order contributions, of order 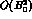 ,
and the constants
,
and the constants 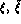 and
and 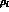 by an amount
by an amount  . In
generalized
. In
generalized 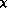 PT, renormalization proceeds order by order in the expansion
in powers of the constant
PT, renormalization proceeds order by order in the expansion
in powers of the constant 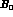 .
.
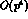 order Lagrangian
order Lagrangian 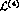 contains 10
low energy constants
contains 10
low energy constants 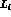 [
[ . As already
pointed out,
. As already
pointed out, 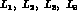 and
and 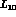 - the constants of
- the constants of
 - play an identical role in both schemes.
- play an identical role in both schemes. 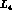 and
and 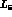 are
related to the constants
are
related to the constants 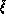 and
and 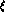 in
in  :
:
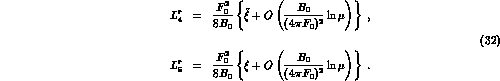
 constants
constants 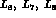 are related to the
are related to the
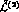 constants
constants 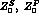 and
and  , respectively :
, respectively :
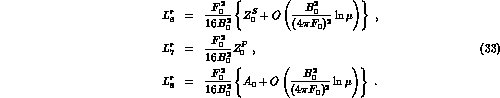
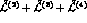 involves additional terms, not contained in
involves additional terms, not contained in 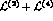 , and which the standard
, and which the standard  PT relegates to higher
orders d>4. Setting the corresponding additional constants to zero, one
recovers the standard
PT relegates to higher
orders d>4. Setting the corresponding additional constants to zero, one
recovers the standard  PT up to and including order
PT up to and including order 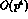 . This
phenomenon is general: Order by order, the standard expansion reappears as a
special case of G
. This
phenomenon is general: Order by order, the standard expansion reappears as a
special case of G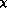 PT.
PT.