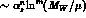 , where
, where 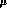 is a scale of the order of the mass of the
decaying hadron. For an accurate estimate of the short-distance
contributions, the large logarithms have to be resummed to all orders using
renormalization group (RG) techniques.
is a scale of the order of the mass of the
decaying hadron. For an accurate estimate of the short-distance
contributions, the large logarithms have to be resummed to all orders using
renormalization group (RG) techniques.
Strong interactions play a crucial role in non-leptonic weak decays. The perturbative
short-distance effects, included in the calculation of the Wilson coefficients, may
be very important because of the presence of large logarithms 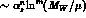 , where
, where 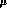 is a scale of the order of the mass of the
decaying hadron. For an accurate estimate of the short-distance
contributions, the large logarithms have to be resummed to all orders using
renormalization group (RG) techniques.
is a scale of the order of the mass of the
decaying hadron. For an accurate estimate of the short-distance
contributions, the large logarithms have to be resummed to all orders using
renormalization group (RG) techniques.
The starting point is the T-product of the two weak currents expanded at short distances in terms of local operators. Taking into account the renormalization effects due to strong interactions, we write
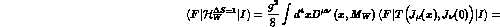
where 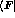 and
and 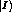 are the generic final and initial states; the
are the generic final and initial states; the 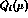 form a complete basis
of operators renormalized at the scale
form a complete basis
of operators renormalized at the scale 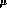 ;
the
;
the 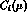 are the corresponding
Wilson coefficients and
the dots represent terms which are suppressed with respect to the dominant ones
as powers of
are the corresponding
Wilson coefficients and
the dots represent terms which are suppressed with respect to the dominant ones
as powers of 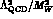 (
(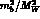 for B-decays).
The effective Hamiltonian is
independent of renormalization scale
for B-decays).
The effective Hamiltonian is
independent of renormalization scale 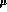 . On the
lattice, the renormalization scale can be replaced by the inverse
lattice spacing
. On the
lattice, the renormalization scale can be replaced by the inverse
lattice spacing
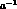 and the effective Hamiltonian can be expressed in terms of bare
lattice operators [9]. The OPE in eq. (34)
must be valid for all possible initial and final
states. This implies that
the effective Hamiltonian is defined from an operator relation
and the effective Hamiltonian can be expressed in terms of bare
lattice operators [9]. The OPE in eq. (34)
must be valid for all possible initial and final
states. This implies that
the effective Hamiltonian is defined from an operator relation
The important features of 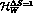 are the following:
are the following:
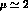 --3 GeV
--3 GeV
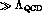 .
In the leading logarithmic approximation (LLA),
all terms of
.
In the leading logarithmic approximation (LLA),
all terms of 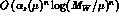 are taken into account;
are taken into account;
Since 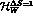 , eq. (35), is
independent of
, eq. (35), is
independent of 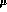 , the coefficients
, the coefficients 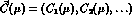 must satisfy the RG equations
must satisfy the RG equations
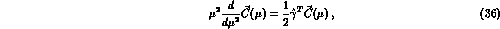
which can be more conveniently written as
where
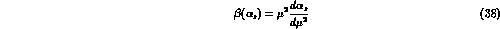
is the QCD  -function and
-function and
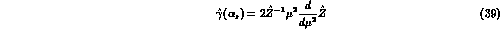
is the anomalous-dimension matrix of the renormalized operators;
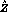 is defined by the relation which
connects the bare operators to the renormalized ones,
is defined by the relation which
connects the bare operators to the renormalized ones,
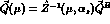 .
.
The solution of the system of linear equations (37) is
found by introducing a suitable
evolution matrix 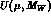 and by imposing an appropriate set of initial
conditions, usually called matching conditions.
The coefficients
and by imposing an appropriate set of initial
conditions, usually called matching conditions.
The coefficients 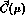 are given by
are given by![]()
with
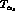 is the ordered product with
increasing couplings from right to left.
The matching conditions are found by imposing that, at
is the ordered product with
increasing couplings from right to left.
The matching conditions are found by imposing that, at 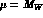 ,
the matrix elements of the original T-product of the currents coincide,
up to terms
suppressed as inverse powers of
,
the matrix elements of the original T-product of the currents coincide,
up to terms
suppressed as inverse powers of 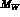 , with the corresponding
matrix elements of
, with the corresponding
matrix elements of 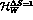 . To this end,
we introduce the vector
. To this end,
we introduce the vector 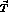 defined by the relation
defined by the relation
where 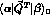 are the matrix elements
of the operators at tree level.
We also introduce the matrix
are the matrix elements
of the operators at tree level.
We also introduce the matrix 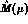 such that
such that

In terms of 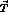 and
and 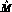 , the matching condition
, the matching condition
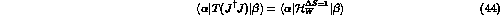
fixes the value of the Wilson coefficients at the scale 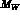
Notice that the matching could be imposed at any scale  ,
such that large logarithms do not appear
in the calculation of the Wilson coefficients at the
scale
,
such that large logarithms do not appear
in the calculation of the Wilson coefficients at the
scale  , i.e.
, i.e. 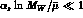 .
.
Equation (40) is correct
if no threshold corresponding to a quark mass
between 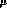 and
and 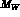 is present. Indeed, as
is present. Indeed, as 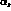 ,
,
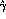 and
and 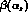 all
depend on the number of active flavours, it is necessary to change
the evolution matrix
all
depend on the number of active flavours, it is necessary to change
the evolution matrix 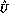 defined in eq.
(41), when passing the threshold.
The general case then corresponds
to a sequence
of effective theories with a decreasing number of ``active'' flavours.
By ``active'' flavour, we mean a dynamical massless
(
defined in eq.
(41), when passing the threshold.
The general case then corresponds
to a sequence
of effective theories with a decreasing number of ``active'' flavours.
By ``active'' flavour, we mean a dynamical massless
(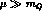 ) quark field. The
theory with k ``active'' flavours is matched to the one with k+1
``active'' flavours at the threshold. This procedure changes the solution
for the Wilson coefficients. For instance, if one starts
with five ``active'' flavours at the scale
) quark field. The
theory with k ``active'' flavours is matched to the one with k+1
``active'' flavours at the threshold. This procedure changes the solution
for the Wilson coefficients. For instance, if one starts
with five ``active'' flavours at the scale 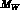 and chooses
and chooses 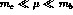 ,
the Wilson coefficients become
,
the Wilson coefficients become
The inclusion of the charm threshold proceeds along the same lines.