


Next: 2 CP-violation in decays
Up: Chapter 1 Section 2
Previous: Chapter 1 Section 2
The understanding of mixing and CP-violation in hadronic systems is one
of the crucial tests of the Standard Model. In the last few years considerable
theoretical and experimental effort has been invested in this subject.
On the theoretical side, the complete next-to-leading expressions
of the relevant effective 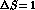 ,
, 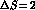 ,
, 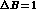 and
and 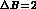 Hamiltonians have been computed [1]--[5],
thus reducing the theoretical uncertainties
Hamiltonians have been computed [1]--[5],
thus reducing the theoretical uncertainties . Moreover, there is now
increasing theoretical evidence that the value of the
pseudoscalar B-meson decay constant is large,
. Moreover, there is now
increasing theoretical evidence that the value of the
pseudoscalar B-meson decay constant is large, 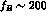 MeV, and that
the B--
MeV, and that
the B--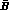 parameter
parameter 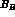 is quite close to one.
This strongly constrains the Cabibbo-Kobayashi-Maskawa parameters and it
has remarkable consequences on CP-violation in B decays,
see refs. [7,8].
Still, the evaluation of hadronic matrix elements is subject to large
uncertainties, that are particularly severe for
is quite close to one.
This strongly constrains the Cabibbo-Kobayashi-Maskawa parameters and it
has remarkable consequences on CP-violation in B decays,
see refs. [7,8].
Still, the evaluation of hadronic matrix elements is subject to large
uncertainties, that are particularly severe for 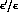 , where
important cancellations of different contributions occur
for large values of the top mass. Indeed, a significative reduction of the
theoretical uncertainty on
, where
important cancellations of different contributions occur
for large values of the top mass. Indeed, a significative reduction of the
theoretical uncertainty on 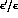 would require a substantial improvement in
the calculation of the hadronic matrix elements, either from
lattice simulations or from other non-perturbative techniques.
would require a substantial improvement in
the calculation of the hadronic matrix elements, either from
lattice simulations or from other non-perturbative techniques.
On the experimental side, more accurate measurements of the
mixing angles are now available and the mass of the top quark,
experimental evidence of which has recently been found by CDF [10], is
constrained within tight limits [11].
Still, in spite
of very accurate measurements, the experimental results for the CP
violating parameter 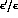 are far from conclusive [12,13].
A better accuracy, at the level of
are far from conclusive [12,13].
A better accuracy, at the level of 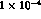 , should be achieved
by the experiments of the next generation.
, should be achieved
by the experiments of the next generation.
In the following, we briefly introduce the  effective Hamiltonian
and summarize the main results of the next-to-leading calculation of the
relevant Wilson coefficients.
An updated analysis of
effective Hamiltonian
and summarize the main results of the next-to-leading calculation of the
relevant Wilson coefficients.
An updated analysis of 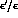 , along the lines followed
in refs. [7]--[9], is presented. Particular emphasis is
devoted to
a realistic evaluation of the uncertainties. We also compare the results of
refs. [7]--[9] to
the next-to-leading order analysis of ref. [14].
In section 2, the basic formulae, which define the CP-violation
parameters
, along the lines followed
in refs. [7]--[9], is presented. Particular emphasis is
devoted to
a realistic evaluation of the uncertainties. We also compare the results of
refs. [7]--[9] to
the next-to-leading order analysis of ref. [14].
In section 2, the basic formulae, which define the CP-violation
parameters  and
and  , are presented;
in section 3, the definition of the
Cabibbo--Kobayashi--Maskawa matrix and the notation used in this work are
introduced;
in sections 4 and 5, we give several details about
the
, are presented;
in section 3, the definition of the
Cabibbo--Kobayashi--Maskawa matrix and the notation used in this work are
introduced;
in sections 4 and 5, we give several details about
the 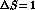 effective Hamiltonian relevant for direct CP-violation. In
particular, the Wilson coefficients in different regularization schemes are
reported.
In section 7, we give the formulae which has been used to obtain
the theoretical predictions; in section 8, the
theoretical predictions from the more recent analyses are given.
Further details, including a theoretical discussion of the
matching conditions, of the B-parameters and of the uncertainties coming
from the choice of
effective Hamiltonian relevant for direct CP-violation. In
particular, the Wilson coefficients in different regularization schemes are
reported.
In section 7, we give the formulae which has been used to obtain
the theoretical predictions; in section 8, the
theoretical predictions from the more recent analyses are given.
Further details, including a theoretical discussion of the
matching conditions, of the B-parameters and of the uncertainties coming
from the choice of 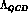 , the renormalization scale, etc. can be
found in ref. [9].
, the renormalization scale, etc. can be
found in ref. [9].



Next: 2 CP-violation in decays
Up: Chapter 1 Section 2
Previous: Chapter 1 Section 2
Carlos E.Piedrafita
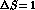 ,
, 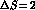 ,
, 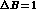 and
and 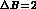 Hamiltonians have been computed [1]--[5],
thus reducing the theoretical uncertainties
Hamiltonians have been computed [1]--[5],
thus reducing the theoretical uncertainties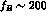 MeV, and that
the B--
MeV, and that
the B--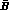 parameter
parameter 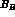 is quite close to one.
This strongly constrains the Cabibbo-Kobayashi-Maskawa parameters and it
has remarkable consequences on CP-violation in B decays,
see refs. [7,8].
Still, the evaluation of hadronic matrix elements is subject to large
uncertainties, that are particularly severe for
is quite close to one.
This strongly constrains the Cabibbo-Kobayashi-Maskawa parameters and it
has remarkable consequences on CP-violation in B decays,
see refs. [7,8].
Still, the evaluation of hadronic matrix elements is subject to large
uncertainties, that are particularly severe for 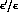 , where
important cancellations of different contributions occur
for large values of the top mass. Indeed, a significative reduction of the
theoretical uncertainty on
, where
important cancellations of different contributions occur
for large values of the top mass. Indeed, a significative reduction of the
theoretical uncertainty on 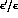 would require a substantial improvement in
the calculation of the hadronic matrix elements, either from
lattice simulations or from other non-perturbative techniques.
would require a substantial improvement in
the calculation of the hadronic matrix elements, either from
lattice simulations or from other non-perturbative techniques.
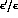 are far from conclusive [
are far from conclusive [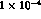 , should be achieved
by the experiments of the next generation.
, should be achieved
by the experiments of the next generation.
 effective Hamiltonian
and summarize the main results of the next-to-leading calculation of the
relevant Wilson coefficients.
An updated analysis of
effective Hamiltonian
and summarize the main results of the next-to-leading calculation of the
relevant Wilson coefficients.
An updated analysis of 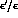 , along the lines followed
in refs. [
, along the lines followed
in refs. [ and
and  , are presented;
in section
, are presented;
in section 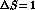 effective Hamiltonian relevant for direct CP-violation. In
particular, the Wilson coefficients in different regularization schemes are
reported.
In section
effective Hamiltonian relevant for direct CP-violation. In
particular, the Wilson coefficients in different regularization schemes are
reported.
In section 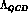 , the renormalization scale, etc. can be
found in ref. [
, the renormalization scale, etc. can be
found in ref. [