Hashing is another important and widely used technique for implementing collections. Conceptually, hashing involves calculating an index from the key or other parts of an element, and then using that index to look for matches in a hash table. The function that calculates the index is called a hash function.
A hash-table implementation variant is suitable for nearly all applications with a balanced mix of operations. Such an implementation is quick for retrieving elements. It can also add and delete elements quickly, because, unlike an AVL tree, it does not need to be rebalanced. The efficiency of a hash-table implementation is largely dependent on the hash function implementation.
You cannot use a hash-table implementation variant when you require your elements to appear in main storage in sorted order (where elements earlier in the sorting order have lower addresses than elements later in the sorting order). On the other hand, you must use a hash table if you have a complex key (one composed, for example, of several attributes of an element), and either you cannot find a reasonable way to compare keys, or the comparison would be expensive.
For collections that do not provide access by key, but that support a hash-table implementation variant, the complete element is used as the input to the hash function.
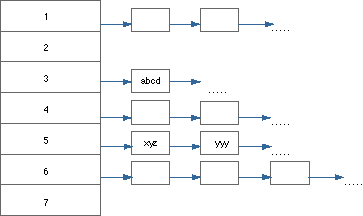
Hashing, as implemented in the collection classes, allows elements to be stored in a potentially unlimited space, and therefore imposes no limit on the size of the collection. The figure below shows a hash-table implementation variant.
Hash-Table Implementation Variant

The hash function that calculates the index 3 from abcd is implemented as follows:
The principal behind a hash table is that the possibly infinite set of elements in your collection is partitioned into a finite number of hash values (1, 2, 3, ...). Your hash function is called with a key and a modulo value, and you use the key and the modulo value to arrive at an integer hash value. If for two different keys the hash function returns the same hash value (as for xyz and yyy in the previous figure), a hash collision occurs. In such cases, a hash implementation constructs a collision list where all keys returning the same hash value are linked.
In the best case, for each different key, your hash function should return a different hash value. At the very least, it is desirable for the collision lists to remain small so that access time is fast. This means that hash values should be evenly distributed. Your hash function should randomly hash the key so that the hash value is not dependent on the key value in any trivial way. Your hash function should always return the same hash value for a given key and modulo provided to it.
![]()
Introduction to the
Collection Classes
Collection Class
Hierarchy
Overall
Implementation Structure
Flat Collections
Trees
AVL Tree
B* Tree
Diluted Table
List
Table
![]()
Class Template
Naming Conventions
Possible
Implementation Paths
Choosing One
of the Provided Implementation Variants
Replacing the
Default Implementation
Taking Advantage
of the Abstract Class Hierarchy
Instantiating
the Collection Classes