AVL trees are a special form of binary tree. You can better understand AVL trees if you know how a binary tree is structured.
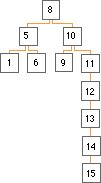
Trees are binary trees when all nodes have either zero, one, or two children. Binary trees are often used in applications where you want to store elements in a certain order. In such cases, the left child always points to an element that comes earlier in the order than the parent node, and the right child points to an element that comes later than the parent. A search through a binary tree begins at the root node. The search then continues downward until the desired element is found, by determining whether a node comes before or after the searched-for node, and then following the appropriate branch. For example, the binary tree shown in the figure below has elements added in the following sequence: 8 - 10 - 5 - 1 - 9 - 6 - 11. A search for element 9 begins at the root node (element 8). Assuming that the element value defines the ordering relation, the search would take the right node from element 8 (because 9 is greater than 8) and would arrive at element 10. The search would take the left node from element 10 (because 9 is smaller than 10) and would arrive at element 9, the desired element.
The following figures show you a binary search tree and an unbalanced binary search tree.
| Balanced Binary Search Tree | Unbalanced Binary Search Tree | |
|---|---|---|
 |
 |
One drawback of a binary search tree is that the tree can easily become unbalanced. The figure shows how unbalanced the tree becomes when the elements 12 through 15 are added. The unbalanced binary tree looks almost like a list, without the performance advantage of a normal binary search tree. To obtain this performance advantage, a binary search tree should always remain balanced. The AVL Tree is a special form of binary search tree that maintains balance.
AVL trees are useful for collections containing a large number of small elements. An AVL tree implementation is even suitable for adding and deleting, because the performance overhead for the rebalancing that sometimes occurs when an element is added or deleted is still less expensive than searching through the elements of a sequence to find the position at which to add or delete an element.
If you use a set collection and do not choose an implementation variant, you are automatically using an AVL tree. If you use a set and are not aware that the set is implemented as an AVL tree, you may be surprised that a set requires an ordering relation, when a set is an unordered collection. The reason a set requires an ordering relation is that an AVL tree requires an ordering relation to determine where to add new elements or where to find elements to be accessed or deleted. As this example shows, required element and key-type functions are determined by two factors:
![]()
Introduction to the
Collection Classes
Collection Class
Hierarchy
Overall
Implementation Structure
Flat Collections
Trees
B* Tree
Diluted Table
Hash Table
List
Table
![]()
Class Template
Naming Conventions
Possible
Implementation Paths
Choosing One
of the Provided Implementation Variants
Replacing the
Default Implementation
Taking Advantage
of the Abstract Class Hierarchy
Instantiating
the Collection Classes