The following flat collections are provided by the Collection Class Library:
The figure below shows the flat collection that results from each combination of properties. For example, Map appears in the Unique, Unordered column for the Key, Element Equality row. This means that a map is unordered, each element is unique, keys are defined, and element equality is defined. This implies that there are no flat collections that have all of the following properties:
The rationale for not implementing collections with these combinations of properties is that there is no reason to choose them over another collection that is already available. For example, for an ordered collection that is sequential and offers access by key, the key access would only have advantages if the elements are stored in a position depending on their key. Because they are not, there is no flat collection with key access that maintains a sequential order.
Unordered |
Ordered |
|||||
|---|---|---|---|---|---|---|
Sorted |
Sequential | |||||
| Unique | Multiple | Unique | Multiple | Multiple | ||
| Key (key equality must be defined) |
Element Equality |
Map |
Relation |
Sorted map |
Sorted relation |
N/A |
No |
Key set |
Key bag |
Key sorted set |
Key sorted bag |
N/A |
|
| No Key | Element Equality |
Set |
Bag |
Sorted set |
Sorted bag |
Equality sequence |
No |
N/A |
Heap |
N/A |
N/A |
Sequence |
|
For example, the default set collection:
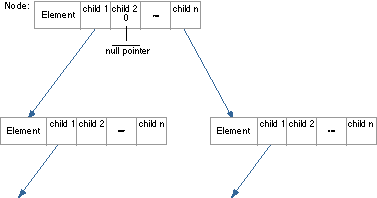
Trees can be described either as structures whose elements have a hierarchy or as a special form of recursive structure. Recursively a tree can be described as a node (parent) with pointers to other nodes (children). Every node has a fixed number of pointers, which are set to null at initialization time. Insertion of a new node involves setting a pointer in the parent so that it points to the inserted child. The figure below illustrates the structure of an n-ary tree.
One node is the entry point to the tree. This node is designated as the root. Nodes without any pointers to other nodes are called leaf nodes or terminal nodes.
The Structure of N-ary Trees

Similarly, you can obtain tree-like or recursive structures by implementing the array of children of a node as a flat collection of nodes. This will give you different functionality for the children, for example, the ability to locate a child with a given value.
Trees in general are more useful for searching elements than for adding and deleting elements. For this reason, they are often called search trees. The descriptions of AVL and B* trees explain why trees are well-suited for searching. Generally, you can locate and insert elements in collections implemented as trees faster than you can in collections implemented as lists. However, if you only want to iterate through elements in a collection, it is faster to iterate through the elements of a list.
![]()
Introduction to the
Collection Classes
Collection Class
Hierarchy
Overall
Implementation Structure
Element
Functions and Key-Type Functions
Collection Class
Polymorphism
Collection
Characteristics
Ordering of
Collection Elements
Access by Key
Equality
Relation
Uniqueness
of Entries
![]()
Defining
Equality Relation
Defining Key
or Element Equality
Defining an
Operations Class
Implementing
Element- and Key-Type Functionality
Defining
Member Functions of the Element Object Type
Defining
Separate Global Functions
Using
or Defining an Element Operation Class
Things
to Watch Out For
Memory
Management with Element Operation Classes
Guard
Objects
Instantiating a Guard Object
Using
Guard Objects
Class
Template Naming Conventions
Possible
Implementation Paths
Choosing One
of the Provided Implementation Variants
Adding an
Element to a Collection
Removing an
Element from a Collection
Copying and
Referencing Collections
Instantiating
the Collection Classes