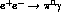 cross section at lowest order is obtained from
cross section at lowest order is obtained from
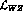 in eq.(25) and turns out to be
in eq.(25) and turns out to be
The 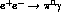 cross section at lowest order is obtained from
cross section at lowest order is obtained from
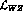 in eq.(25) and turns out to be
in eq.(25) and turns out to be
where s is the square of the total CM energy and 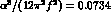 nb. This lowest order cross section is shown
(dotted line) in Fig.(4).
nb. This lowest order cross section is shown
(dotted line) in Fig.(4).
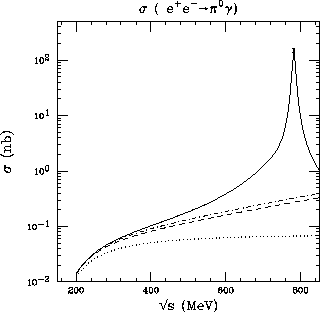
Figure 4:
Cross-section for 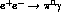 as a function of
the total CM energy : lowest order result (dots), including
counter-term contributions at the next order (dashes),
full ChPT prediction (with loop and counterterm
corrections) at next-to leading order (dot-dashes) and
the ``all-order'' result (full line).
as a function of
the total CM energy : lowest order result (dots), including
counter-term contributions at the next order (dashes),
full ChPT prediction (with loop and counterterm
corrections) at next-to leading order (dot-dashes) and
the ``all-order'' result (full line).
Next order corrections in ChPT include the effects
of loops and counterterms as in eq.(28). For the latter, the
resonance saturation assumption implies 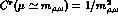 , thus increasing the lowest order amplitude
up to a
, thus increasing the lowest order amplitude
up to a 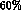 at
at 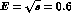 GeV as also shown (dashed line) in
Fig.(4).
The associated loop corrections are given by
GeV as also shown (dashed line) in
Fig.(4).
The associated loop corrections are given by 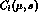 in eq.(29).
These loop corrections are considerably smaller
than those coming from the corresponding counterterms (around a 15% in the
amplitude) and slightly increase the
in eq.(29).
These loop corrections are considerably smaller
than those coming from the corresponding counterterms (around a 15% in the
amplitude) and slightly increase the 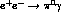 cross-section,
as shown (dot-dashed line) in Fig.(4). This curve represents the
full ChPT
prediction at next-to-leading order for
cross-section,
as shown (dot-dashed line) in Fig.(4). This curve represents the
full ChPT
prediction at next-to-leading order for 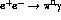 and is
expected to reproduce future data in the low energy region.
and is
expected to reproduce future data in the low energy region.
Around the
resonance masses the cross-section is quite different as indicated by the
value at the  -peak [20]
-peak [20] 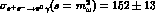 nb,
shown with error bars in Fig.(4).
Attempts
to improve the situation in ChPT would imply the evaluation of higher order
loop corrections and the corresponding counterterms. In general and for
values of
nb,
shown with error bars in Fig.(4).
Attempts
to improve the situation in ChPT would imply the evaluation of higher order
loop corrections and the corresponding counterterms. In general and for
values of 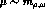 , next order loop corrections in ChPT are
found to be around 10-
, next order loop corrections in ChPT are
found to be around 10-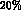 of the preceding order amplitude,
smaller than those coming from other uncertainties in our model
and the values of its parameters.
By contrast, corrections coming from counterterms have been shown to be
larger than the ones from the loops
and the evaluation of higher-order ones, under our assumption of
resonance saturation, is trivial.
As before, the introduction of the whole vector-meson form-factor
of the preceding order amplitude,
smaller than those coming from other uncertainties in our model
and the values of its parameters.
By contrast, corrections coming from counterterms have been shown to be
larger than the ones from the loops
and the evaluation of higher-order ones, under our assumption of
resonance saturation, is trivial.
As before, the introduction of the whole vector-meson form-factor
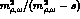 (instead of its truncated series
(instead of its truncated series
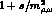 ) represents an ``all-order'' estimate of our
resonance dominated counterterms. Taking into account the physical finite
widths of the
) represents an ``all-order'' estimate of our
resonance dominated counterterms. Taking into account the physical finite
widths of the 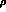 and
and  mesons, this amounts to write
mesons, this amounts to write
to first order in the loop corrections.
The corresponding prediction is also shown (solid line) in
Fig.(4). The agreement
at the  -peak (161 nb vs
-peak (161 nb vs 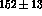 nb from experiment
[20]) is essentially a consequence of having used
nb from experiment
[20]) is essentially a consequence of having used 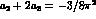 , and
, and 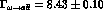 MeV and
MeV and  [13], quite close to
[13], quite close to 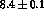 MeV and
MeV and
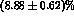 as measured in [20] from the
as measured in [20] from the 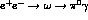 cross-section at the
cross-section at the  peak. Near this peak the
peak. Near this peak the
 -contribution is obviously dominant, but at lower energies, loop
effects, counterterms and the
-contribution is obviously dominant, but at lower energies, loop
effects, counterterms and the 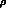 resonance curve represent a substantial
fraction of the total cross-section.
resonance curve represent a substantial
fraction of the total cross-section.
The 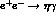 cross-section can be analyzed along the same
lines. Eq.(48) becomes
cross-section can be analyzed along the same
lines. Eq.(48) becomes
and the various contributions arising from this expression have been plotted in Fig.(5), with the same notation employed for Fig.(4).
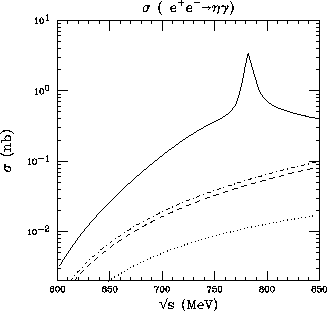
Figure 5: Cross-section for 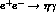 as a function of
the CM energy, distinguishing different contributions near and
around the omega peak from
lowest order(dots), counterterms (dashes) and chiral loops (dotdashes).
as a function of
the CM energy, distinguishing different contributions near and
around the omega peak from
lowest order(dots), counterterms (dashes) and chiral loops (dotdashes).
The interference effects among the various terms are now important
even on the  -peak.
Experimental data for
-peak.
Experimental data for 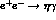 in this energy region are
known [20] but affected by large error bars.
in this energy region are
known [20] but affected by large error bars.
Turning now to the 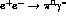 transition,
transition,  , allowing
for the final state photon to be also off-mass-shell (
, allowing
for the final state photon to be also off-mass-shell (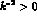 ) as in
) as in
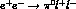 , one gets
, one gets
Eq.(48) leads to the
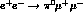 cross-section plotted in Fig.(6) for
cross-section plotted in Fig.(6) for
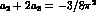 and
and 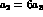 ,
, 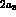 and 0 (dashed, solid and
dotted lines). One obtains an
and 0 (dashed, solid and
dotted lines). One obtains an  -peak cross-section
-peak cross-section 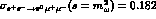 ,
, 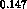 and
and  nb,
respectively.
nb,
respectively.
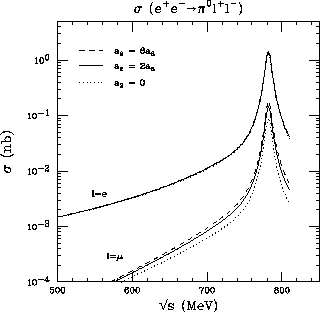
Figure 6: Cross-section for 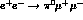 and
and
 for the quoted values of
for the quoted values of 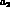 and
and 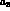 . VMD (solid line)
requires
. VMD (solid line)
requires 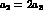 . The dashed line corresponds
to the alternative model with
. The dashed line corresponds
to the alternative model with 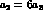 .
.
The corresponding experimental value 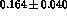 nb
[20,17]
favours the first two possibilities but new experiments could
contribute to clarify the situation discriminating among the different ratios
nb
[20,17]
favours the first two possibilities but new experiments could
contribute to clarify the situation discriminating among the different ratios
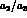 . This is not the case for the
. This is not the case for the
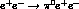 cross-section (also shown in
Fig.(6)) where the
predictions for different values of
cross-section (also shown in
Fig.(6)) where the
predictions for different values of 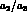 are quite similar due to the
dominance of small
are quite similar due to the
dominance of small 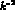 values which reduces the sensitivity on
values which reduces the sensitivity on
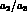 as seen in eq.(48).
Moreover, for this particular process and well below the resonance region
one could expect non-negligible contributions coming from the scattering
channel
as seen in eq.(48).
Moreover, for this particular process and well below the resonance region
one could expect non-negligible contributions coming from the scattering
channel  with two spacelike photons [19].
with two spacelike photons [19].
In summary, 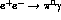 ,
, 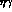 and
and
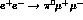 cross-sections at low energy seem particularly interesting to test
the saturation of the ChPT counterterms by resonances, which in
this case are expected to be the well-known
cross-sections at low energy seem particularly interesting to test
the saturation of the ChPT counterterms by resonances, which in
this case are expected to be the well-known  and
and
 vector-mesons.
vector-mesons.