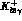The matrix element for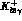 
has the general structure
The diagram of Fig. 4.1.a corresponding to the first part of
Eq. (4.1) includes Bremsstrahlung off the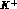 
.
The lepton Bremsstrahlung diagram of Fig. 4.1.b is represented
by the second part of Eq. (4.1).
The hadronic tensors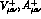 
are defined as
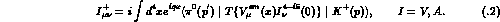
is the 
matrix element
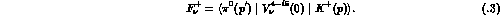
The tensors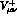 
and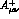 
satisfy the Ward identities
leading in turn to
as is required by gauge invariance.
For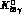 
, one obtains the corresponding amplitudes and
hadronic tensors by making the replacements
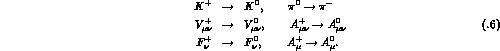
To make the infrared behaviour transparent,
it is convenient to separate the tensors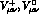 
into two parts:
Due to Low's theorem, the amplitudes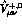 
are finite for 
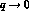. The axial amplitudes
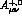are automatically infrared finite.
The Ward identity (4.4) implies that the vector amplitudes
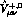are transverse:
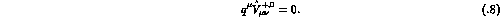
For on-shell photons, Lorentz and parity invariance together with gauge invariance allow the general decomposition (dropping the superscripts +,0 and terms that vanish upon contraction with the photon polarization vector)
With the decomposition (4.7) we can write the matrix element
for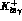 
in (4.1) in a form analogous to Eq.
(1.2) for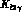 
:
The four invariant vector a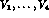mplitudes 
and
the four axial amplitudes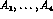 
are functions of three scalar
variables. A convenient choice for these variables is
where W is the invariant mass of the lepton pair. The amplitudes
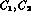can be expressed in terms of the 
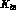form factors
and depend only on the variable
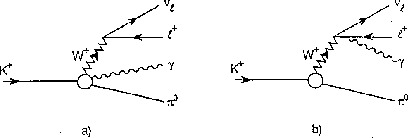
Figure 4.1: Diagrammatic representation of the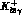 
amplitude.
.
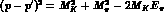For the full kinematics of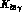 
two more variables are
needed, e.g.
The variable x is related to the angle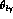 
between the
photon and the charged lepton in the K rest frame:
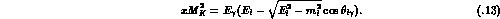
T invariance implies that the vector amplitudes 
, the
axial amplitudes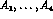 
and the 
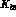form factors
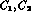are (separately) relatively real in the physical region.
We choose the standard
phase convention in which all amplitudes are real.
For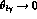 
(collinear lepton and photon), there is
a lepton mass singularity in (4.1) which is numerically
relevant for l = e.
The region of small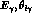 
is dominated by the
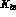matrix elements. The new theoretical information of
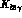decays resides in the tensor amplitudes
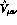and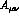 
. The relative importance of these
contributions can be enhanced by cutting away the region of low
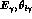. It may turn out to be of advantage to
reduce the statistics by applying more severe cuts than necessary from
a purely experimental point of view.
