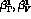 coefficients
we study the
coefficients
we study the 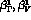 behaviour of the vector-vector correlation
function where one can compare the theoretical predictions with
experimental results.
behaviour of the vector-vector correlation
function where one can compare the theoretical predictions with
experimental results.
To estimate the values of the 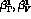 coefficients
we study the
coefficients
we study the 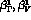 behaviour of the vector-vector correlation
function where one can compare the theoretical predictions with
experimental results.
behaviour of the vector-vector correlation
function where one can compare the theoretical predictions with
experimental results.
The two-point vector correlation function is defined as

where 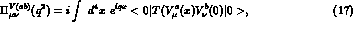 is the flavoured vector quark current:
is the flavoured vector quark current:

with
 the Gell-Mann matrices normalized as
the Gell-Mann matrices normalized as 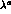 .
Lorentz covariance and
.
Lorentz covariance and  invariance imply for the
invariance imply for the
 the following structure:
the following structure:

where 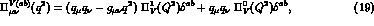 , with
, with 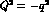 euclidean.
euclidean.
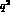 is zero at all orders in the chiral limit.
For
is zero at all orders in the chiral limit.
For 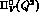 the following expression holds at NPLL order [1]:
the following expression holds at NPLL order [1]:
where the running of 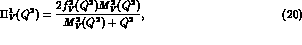 and
and 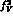 at NPLL order can be
extracted from eq. (14) with
at NPLL order can be
extracted from eq. (14) with 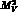 terms set to zero.
terms set to zero.
The real part of the invariant 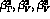 function is related to
its imaginary part through a standard dispersion relation
function is related to
its imaginary part through a standard dispersion relation

For a review on QCD spectral Sum rules and the calculation of QCD two-point
Green's functions see [5].
The imaginary part is given in terms of the experimentally known total
hadronic ratio of the 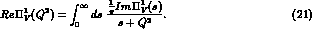 annihilation in the isovector channel
annihilation in the isovector channel

with
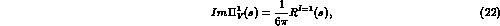
We have performed a comparison between the QR model parametrization
(20), valid in the energy region 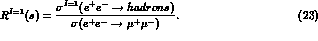 ,
and the prediction obtained from a
modelization of the experimental data on
,
and the prediction obtained from a
modelization of the experimental data on  [6]
in the channel with the
[6]
in the channel with the 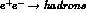 meson quantum numbers (I=1, J=1).
For a determination of the function
meson quantum numbers (I=1, J=1).
For a determination of the function 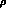 in the
high
in the
high 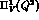 region (i.e. beyond the cutoff
region (i.e. beyond the cutoff 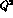 ) see [7].
) see [7].
We adopted the following parametrization of the experimental hadronic isovector ratio:
This is a generalization of the one proposed in ref. [8], where
corrections due to the finite width of the rho meson have not been included.
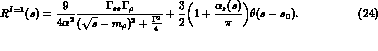 KeV is the
KeV is the  width and
width and
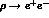 is the total widht of the neutral
is the total widht of the neutral  [9].
We used the leading logarithmic approximation for
[9].
We used the leading logarithmic approximation for 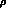 :
:

Expression (24) includes a dependence of
the 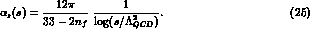 channel upon the
channel upon the 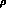 width and the contribution from the
continuum starting at a threshold
width and the contribution from the
continuum starting at a threshold 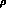 [8].
For the running of
[8].
For the running of 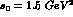 we used a value of 260 MeV
for
we used a value of 260 MeV
for 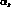 , according to the average experimental value
, according to the average experimental value
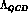 MeV [9] and with
MeV [9] and with 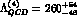 flavours.
flavours.
The results are practically insensitive to the
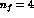 running corrections and our leading log approximation turns
out to be adequate.
running corrections and our leading log approximation turns
out to be adequate.
To extract information on 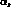 coefficients of
the NTL logarithmic corrections
we made a best fit of the first derivative of the 2-point function coming
from the parametrization (24) of the experimental data:
coefficients of
the NTL logarithmic corrections
we made a best fit of the first derivative of the 2-point function coming
from the parametrization (24) of the experimental data:

where the derivative of the VV function in the QR model is given by:
We have used
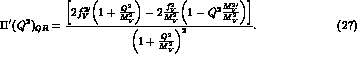 MeV for the IR cutoff and
MeV for the IR cutoff and 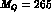 GeV for
the UV cutoff, determined by a global fit in ref. [2].
GeV for
the UV cutoff, determined by a global fit in ref. [2].
In fig.(1) we show the 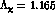 behaviour of the derivative
of the experimental 2-point function, the curve from the best fit,
which has been done in the region:
behaviour of the derivative
of the experimental 2-point function, the curve from the best fit,
which has been done in the region:  GeV, and
the derivative of the ENJL prediction with quark-bubbles resummation.
GeV, and
the derivative of the ENJL prediction with quark-bubbles resummation.
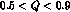
Figure 1:
The derivative of the experimental vector invariant function  (solid line)
the curve from the best fit in the region
(solid line)
the curve from the best fit in the region 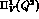 GeV (dashed line)
and the ENJL prediction (dot-dashed line).
GeV (dashed line)
and the ENJL prediction (dot-dashed line).
The best values of the two free coefficients are
The 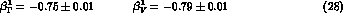 of the fit has been defined as
of the fit has been defined as 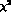 and the
and the 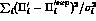 are defined assuming a
are defined assuming a
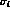 of uncertainty on the experimental data.
A
of uncertainty on the experimental data.
A 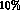 has been obtained.
The ENJL prediction differs by roughly a
has been obtained.
The ENJL prediction differs by roughly a 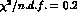 from the experimental curve
at 0.8 GeV. Most of this discrepancy can be accounted for with the
corrections that we have calculated.
from the experimental curve
at 0.8 GeV. Most of this discrepancy can be accounted for with the
corrections that we have calculated.
The invariant function 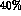 obtained from the best fit automatically
match the ENJL function at
obtained from the best fit automatically
match the ENJL function at 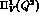 , because we have normalized the
corrections to vanish at
, because we have normalized the
corrections to vanish at 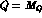 :
:
The
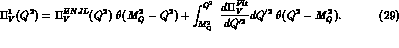 function obtained with the values (28) and with the
matching of eq. (29) is plotted in fig.(2) and compared
with the ENJL prediction (i.e. including the resummation
of linear chains of quark bubbles and including only logarithmic corrections).
function obtained with the values (28) and with the
matching of eq. (29) is plotted in fig.(2) and compared
with the ENJL prediction (i.e. including the resummation
of linear chains of quark bubbles and including only logarithmic corrections).
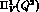
Figure 2:
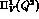 from the QR model (dashed line), obtained from the
fitted derivative of fig. (1) by imposing the matching
with the ENJL function at
from the QR model (dashed line), obtained from the
fitted derivative of fig. (1) by imposing the matching
with the ENJL function at 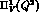 , versus
, versus 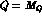 from the ENJL model (solid line).
from the ENJL model (solid line).
The difference between the two curves reaches a 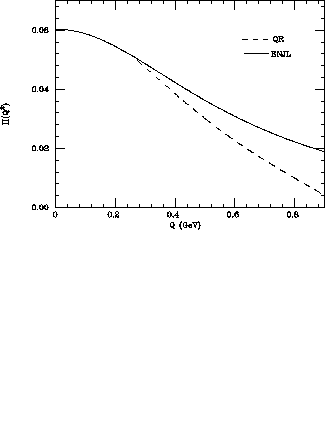 at 0.7 GeV.
at 0.7 GeV.