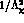 ) is:
) is:
The leading
non anomalous Lagrangian with one vector meson (i.e. of order 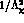 ) is:
) is:
and corresponds to the so called Conventional Vector model [3,4].
The parameters which enter the calculation of the vector two-point function
are the vector mass 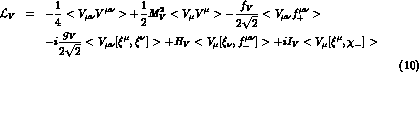 and the coupling
and the coupling 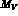 to the external vector
source.
The full Lagrangian up to
to the external vector
source.
The full Lagrangian up to 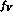 order which gives contribution to
order which gives contribution to
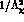 and
and 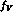 , the vector wave function renormalization constant,
(or equivalently to
, the vector wave function renormalization constant,
(or equivalently to 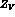 ) is:
) is:
The first term defines the inverse free fermion propagator 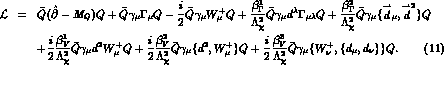 . The remaining part defines the local perturbation to the free Lagrangian
up to order
. The remaining part defines the local perturbation to the free Lagrangian
up to order 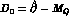 .
There are five
.
There are five 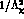 terms with new coefficients
terms with new coefficients  .
Each term can be traced back to the corresponding term in the list
(8) where the covariant derivative
.
Each term can be traced back to the corresponding term in the list
(8) where the covariant derivative 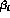 is defined in terms of the
covariant derivative
is defined in terms of the
covariant derivative 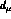 as follows:
as follows:

The covariant derivative on the vector-like fields 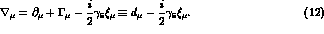 is defined as:
is defined as:

The general formula resulting for 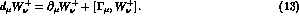 and
and 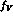 and including the leading
contribution from the ENJL model can be written as follows:
and including the leading
contribution from the ENJL model can be written as follows:
where the wave function renormalization constant 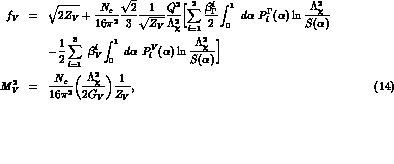 is given by:
is given by:
The 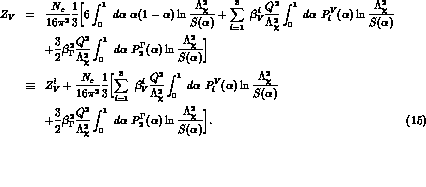 coefficients must be determined from experimental
data.
The function
coefficients must be determined from experimental
data.
The function 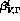 is equal to
is equal to 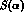 .
The
.
The 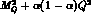 are polynomials in the Feynman
parameter
are polynomials in the Feynman
parameter 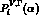 .
Their explicit expression is given by:
.
Their explicit expression is given by:
From eq.(16) one obtains that the purely divergent contribution
(i.e. 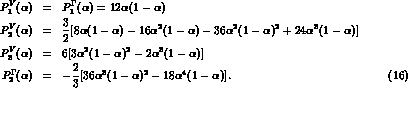 ) to
) to
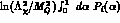 terms is identically zero.
terms is identically zero.
We are left with two independent coefficients: 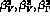 .
.