


Next: References
Up: Chapter 1 Section 3
Previous: 2 decays
The 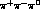 decay of the
decay of the 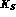 is in principle not forbidden by CP
conservation. It is so, however, at the centre of the Dalitz plot, where
symmetry in pion momenta forbids the appearance of odd values of the relative
angular momenta.
is in principle not forbidden by CP
conservation. It is so, however, at the centre of the Dalitz plot, where
symmetry in pion momenta forbids the appearance of odd values of the relative
angular momenta. 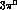 decay of
decay of 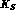 is altogether CP violating.
is altogether CP violating.
Taking into account the mass-matrix mixing effect, one writes:
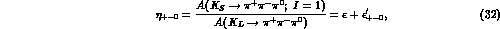
and similarly for the decay 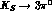 , with an analogous
definition of
, with an analogous
definition of 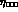 and
and  .
.
Theoretical analyses of the direct CP violation parameters,
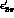 , proceed along much similar lines to those
discussed previously for charged kaon decays
(see, e.g., Refs. [4,7,8]). In lowest order
, proceed along much similar lines to those
discussed previously for charged kaon decays
(see, e.g., Refs. [4,7,8]). In lowest order 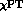 ,
one finds [4]:
,
one finds [4]:
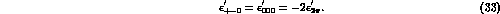
The more recent discussions [7,8,20] include the electroweak
penguin contributions, as well as higher order chiral corrections.
Analogously to the charged kaon case, it seems
unlikely that the lowest order prediction (33) can be
increased by more than one order of magnitude. In this case, the
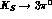 branching ratio is predicted to be:
branching ratio is predicted to be:
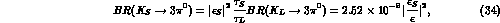
to be compared with the present experimental limit 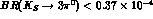 [21]
[21]
For 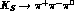 , the problem is the presence of the CP
conserving amplitude which can obscure the CP violating one. Since CP
conserving and CP violating amplitudes do not interfere in the total rate
due to their different dependences on the kinematical variables, the effect of
(mass-mixing) CP violation in the rate for this channel is of order
, the problem is the presence of the CP
conserving amplitude which can obscure the CP violating one. Since CP
conserving and CP violating amplitudes do not interfere in the total rate
due to their different dependences on the kinematical variables, the effect of
(mass-mixing) CP violation in the rate for this channel is of order
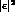 , bringing it down to the level of
, bringing it down to the level of
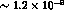 .
.
A possible strategy to search for this effect at DA NE should be the
measurement of the time interference between
NE should be the
measurement of the time interference between 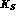 and
and 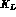 amplitudes, as
discussed in [2]. Concerning the expected sensitivity on
amplitudes, as
discussed in [2]. Concerning the expected sensitivity on
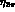 , it is difficult to assess it without a detailed simulation.
As an indication, on statistical grounds the sensitivity should be of the
order of
, it is difficult to assess it without a detailed simulation.
As an indication, on statistical grounds the sensitivity should be of the
order of 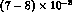 , which is rather far
from the expected value
, which is rather far
from the expected value 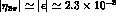 . On the other hand, the most recent experimental findings
are [22]:
. On the other hand, the most recent experimental findings
are [22]:
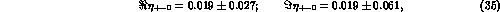
from an unconstrained fit to the data, and
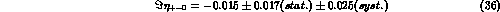
if the
theoretical constraint 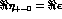 is used in such a fit.
Thus, it might still be worthwhile to make an attempt to obtain an alternative
experimental limit at DA
is used in such a fit.
Thus, it might still be worthwhile to make an attempt to obtain an alternative
experimental limit at DA NE.
NE.
In the decay 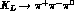 , the mass-mixing CP violating
amplitude is suppressed by an angular momentum barrier and by the
, the mass-mixing CP violating
amplitude is suppressed by an angular momentum barrier and by the
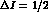 rule, analogously to the CP conserving amplitude of the
rule, analogously to the CP conserving amplitude of the
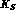 decay into the same channel. This CP violation should manifest itself
in the appearance of the term linear in X, i.e.
decay into the same channel. This CP violation should manifest itself
in the appearance of the term linear in X, i.e. 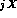 , in
the Dalitz plot (1). This term should arise from the
interference between CP-even and CP-odd
, in
the Dalitz plot (1). This term should arise from the
interference between CP-even and CP-odd 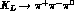 amplitudes.
According to the estimate of [23], the order of magnitude of
the CP-violating coefficient j
should be
amplitudes.
According to the estimate of [23], the order of magnitude of
the CP-violating coefficient j
should be 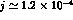 , while the present determination is
, while the present determination is
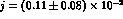 [21]. Thus, the statistics
at DA
[21]. Thus, the statistics
at DA NE would be somewhat marginal to the predicted value for this
parameter. Nonetheless, a significant improvement of the present experimental
value might still be possible.
NE would be somewhat marginal to the predicted value for this
parameter. Nonetheless, a significant improvement of the present experimental
value might still be possible.



Next: References
Up: Chapter 1 Section 3
Previous: 2 decays
Carlos E.Piedrafita
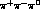 decay of the
decay of the 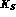 is in principle not forbidden by CP
conservation. It is so, however, at the centre of the Dalitz plot, where
symmetry in pion momenta forbids the appearance of odd values of the relative
angular momenta.
is in principle not forbidden by CP
conservation. It is so, however, at the centre of the Dalitz plot, where
symmetry in pion momenta forbids the appearance of odd values of the relative
angular momenta. 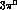 decay of
decay of 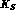 is altogether CP violating.
is altogether CP violating.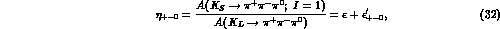
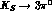 , with an analogous
definition of
, with an analogous
definition of 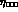 and
and  .
. 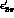 , proceed along much similar lines to those
discussed previously for charged kaon decays
(see, e.g., Refs. [
, proceed along much similar lines to those
discussed previously for charged kaon decays
(see, e.g., Refs. [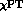 ,
one finds [
,
one finds [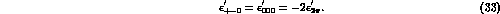
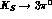 branching ratio is predicted to be:
branching ratio is predicted to be:
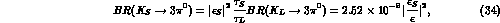
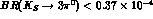 [
[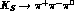 , the problem is the presence of the CP
conserving amplitude which can obscure the CP violating one. Since CP
conserving and CP violating amplitudes do not interfere in the total rate
due to their different dependences on the kinematical variables, the effect of
(mass-mixing) CP violation in the rate for this channel is of order
, the problem is the presence of the CP
conserving amplitude which can obscure the CP violating one. Since CP
conserving and CP violating amplitudes do not interfere in the total rate
due to their different dependences on the kinematical variables, the effect of
(mass-mixing) CP violation in the rate for this channel is of order
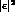 , bringing it down to the level of
, bringing it down to the level of
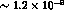 .
. NE should be the
measurement of the time interference between
NE should be the
measurement of the time interference between 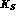 and
and 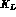 amplitudes, as
discussed in [
amplitudes, as
discussed in [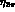 , it is difficult to assess it without a detailed simulation.
As an indication, on statistical grounds the sensitivity should be of the
order of
, it is difficult to assess it without a detailed simulation.
As an indication, on statistical grounds the sensitivity should be of the
order of 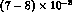 , which is rather far
from the expected value
, which is rather far
from the expected value 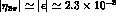 . On the other hand, the most recent experimental findings
are [
. On the other hand, the most recent experimental findings
are [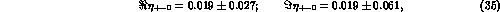
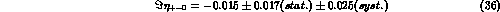
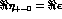 is used in such a fit.
Thus, it might still be worthwhile to make an attempt to obtain an alternative
experimental limit at DA
is used in such a fit.
Thus, it might still be worthwhile to make an attempt to obtain an alternative
experimental limit at DA NE.
NE.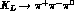 , the mass-mixing CP violating
amplitude is suppressed by an angular momentum barrier and by the
, the mass-mixing CP violating
amplitude is suppressed by an angular momentum barrier and by the
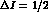 rule, analogously to the CP conserving amplitude of the
rule, analogously to the CP conserving amplitude of the
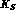 decay into the same channel. This CP violation should manifest itself
in the appearance of the term linear in X, i.e.
decay into the same channel. This CP violation should manifest itself
in the appearance of the term linear in X, i.e. 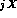 , in
the Dalitz plot (
, in
the Dalitz plot (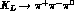 amplitudes.
According to the estimate of [
amplitudes.
According to the estimate of [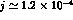 , while the present determination is
, while the present determination is
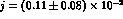 [
[ NE would be somewhat marginal to the predicted value for this
parameter. Nonetheless, a significant improvement of the present experimental
value might still be possible.
NE would be somewhat marginal to the predicted value for this
parameter. Nonetheless, a significant improvement of the present experimental
value might still be possible.