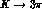 can be expanded in powers of the
independent kinematical variables as follows (higher powers are not requested
by experimental data):
can be expanded in powers of the
independent kinematical variables as follows (higher powers are not requested
by experimental data):
In this case one can study CP-odd charge asymmetries in the total rates and
in the linear slope of the Dalitz plot. Referring to [3] for more
details on the kinematics and the relevant definitions, we recall that,
due to the smallness of the outgoing pion energies, in general the
Dalitz plot distributions for 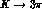 can be expanded in powers of the
independent kinematical variables as follows (higher powers are not requested
by experimental data):
can be expanded in powers of the
independent kinematical variables as follows (higher powers are not requested
by experimental data):
Here, for the process
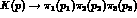 , Y and X are the familiar
kinematical variables,
, Y and X are the familiar
kinematical variables, 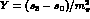 and
and 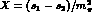 ,
with
,
with 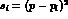 ,
, 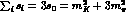 , and `3'
indicates the `odd charge' pion. The term linear in X in
Eq. (1) is CP violating and can appear only in the case of
, and `3'
indicates the `odd charge' pion. The term linear in X in
Eq. (1) is CP violating and can appear only in the case of
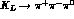 , so that it is not relevant here.
For
, so that it is not relevant here.
For 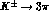 decays the charge asymmetries are then defined as
the relative differences
decays the charge asymmetries are then defined as
the relative differences
and
for both  (i.e.
(i.e. 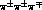 ) and
) and  (i.e.
(i.e. 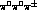 ) decay modes.
) decay modes.
We expand the relevant 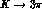 amplitudes up to linear terms. Assuming
amplitudes up to linear terms. Assuming
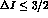 , and including imaginary parts
originating from final state strong interaction effects, this expansion can
be written as
, and including imaginary parts
originating from final state strong interaction effects, this expansion can
be written as
where 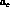 ,
, 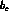 ,
, 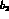 can be chosen as real constants if CP is conserved,
and
can be chosen as real constants if CP is conserved,
and 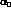 ,
, 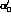
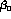 and
and  are also real.
With these definitions,
are also real.
With these definitions, 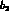 is purely
is purely 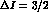 , so that the
, so that the
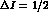 rule would imply the condition:
rule would imply the condition:
Furthermore, lowest order in chiral perturbation theory and the
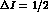 rule give:
rule give:
In the presence of direct CP violation, the coefficients 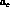 ,
, 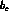 and
and
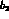 are complex numbers, and nonvanishing charge asymmetries such as
(2) and (3) are generated. For example, specializing
to the centre of the Dalitz plot, for the
are complex numbers, and nonvanishing charge asymmetries such as
(2) and (3) are generated. For example, specializing
to the centre of the Dalitz plot, for the  -decay slope asymmetry
we obtain:
-decay slope asymmetry
we obtain:
where the quantities in the denominators are taken in the CP-exact limit and
therefore are understood to be real. Notice that 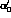 , which
appears in (4), does not contribute to the charge asymmetry
(7).
, which
appears in (4), does not contribute to the charge asymmetry
(7).
The r.h.s. of Eq. (7), and the analogous asymmetry for  decay, explicitly vanish in the limit in which relations (5) and
(6) are obeyed, since in that case there is only one weak decay
amplitude whose phase can be transformed away [4,5].
decay, explicitly vanish in the limit in which relations (5) and
(6) are obeyed, since in that case there is only one weak decay
amplitude whose phase can be transformed away [4,5].
The effective Hamiltonian at the constituent quark level consists, in fact,
of various components, transforming according to the 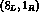 ,
,
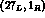 and
and 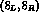 representations of chiral
representations of chiral
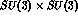 .
.
If the t quark mass were small, the 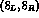 component,
which arises from the electroweak penguin diagrams, could be safely neglected.
In this case, in lowest order
component,
which arises from the electroweak penguin diagrams, could be safely neglected.
In this case, in lowest order 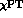 a non-vanishing asymmetry
would arise solely from the interference of the
a non-vanishing asymmetry
would arise solely from the interference of the 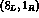 and
and 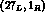 amplitudes, and, in this limit, would be necessarily suppressed by the small
ratio
amplitudes, and, in this limit, would be necessarily suppressed by the small
ratio
quite similar to 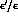 . With
. With 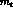 very large, of the
order of
very large, of the
order of 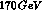 , the effect of the electroweak operators becomes
non-negligible. This rise of the
, the effect of the electroweak operators becomes
non-negligible. This rise of the 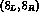 contribution with
contribution with 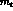 is in fact responsible for the decrease of the Standard Theory prediction of
is in fact responsible for the decrease of the Standard Theory prediction of
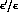 (for more quantitative details, see
[1]).
As for the
(for more quantitative details, see
[1]).
As for the 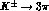 charge asymmetry, it turns out that the contribution
of the
charge asymmetry, it turns out that the contribution
of the 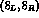 operator increases the leading order prediction of
operator increases the leading order prediction of
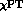 for the Dalitz plot slope asymmetry, and decreases the
prediction for the asymmetry of the widths. Another source of corrections to
the lowest order
for the Dalitz plot slope asymmetry, and decreases the
prediction for the asymmetry of the widths. Another source of corrections to
the lowest order 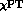 prediction is the isospin breaking
u-d quark mass difference, which feeds contributions proportional
to the (large) coefficient of the
prediction is the isospin breaking
u-d quark mass difference, which feeds contributions proportional
to the (large) coefficient of the 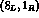 component into the
component into the 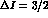 channel.
channel.
Making contact with Ref. [6], we describe now with some detail the
lowest order 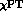 calculation, accounting for the electroweak
penguin diagram contribution and for isospin breaking corrections (see also
[7,8]). The first ingredient is the evaluation of strong
interaction rescattering phases. One finds in
calculation, accounting for the electroweak
penguin diagram contribution and for isospin breaking corrections (see also
[7,8]). The first ingredient is the evaluation of strong
interaction rescattering phases. One finds in
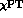 [9,6] to one loop:
[9,6] to one loop:
where 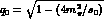 .
.
As it has been introduced in [3], the 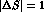 effective Hamiltonian now consists of the familiar
effective Hamiltonian now consists of the familiar 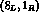 and
and
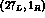 components, represented in leading order
components, represented in leading order 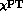 as
[10]
as
[10]
plus the 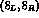 component [9]:
component [9]:
where 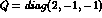 ,
, 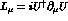 , and
, and
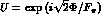 with
with  the pseudoscalar
meson
the pseudoscalar
meson 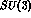 matrix.
matrix.
In terms of the coefficients 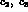 and
and 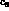 one has:
one has:![]()
where 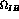 represents the effect of isospin breaking, and numerically
we shall use
represents the effect of isospin breaking, and numerically
we shall use 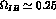 .
.
CP violation is related to the imaginary parts of the coefficients
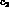 ,
, 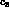 and
and 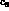 . Introducing for convenience the dimensionless
quantities:
. Introducing for convenience the dimensionless
quantities:
one can express the asymmetry as a superposition of the 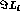 with
coefficients determined by the experimental (real) amplitudes. In turn,
the
with
coefficients determined by the experimental (real) amplitudes. In turn,
the 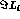 are derived from a theoretical determination of the matrix
elements of the various components of the effective Hamiltonian (
are derived from a theoretical determination of the matrix
elements of the various components of the effective Hamiltonian (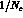 expansion [8], or Lattice QCD
[11,12,13,14]).
expansion [8], or Lattice QCD
[11,12,13,14]).
Eq. (7) then takes the form
where numerically:
The values of 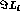 needed in (19) are obtained,
as in Ref. [6], by combining the short-distance, perturbative QCD
coefficients in the expansion of the nonleptonic
needed in (19) are obtained,
as in Ref. [6], by combining the short-distance, perturbative QCD
coefficients in the expansion of the nonleptonic 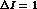 Hamiltonian
in terms of four-quark operators, with the
nonperturbative B-factors computed in Lattice QCD [14].
Hamiltonian
in terms of four-quark operators, with the
nonperturbative B-factors computed in Lattice QCD [14].
As an indication, in Figs. 1 and 2 we represent the results which would be
obtained for the  slope asymmetry (3), by applying
the same kind of numerical analysis performed for
slope asymmetry (3), by applying
the same kind of numerical analysis performed for
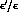 in Ref. [1]. This analysis should
account for the most recent determinations of the Standard Model parameters
(
in Ref. [1]. This analysis should
account for the most recent determinations of the Standard Model parameters
(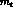 , CKM matrix elements,
, CKM matrix elements, 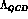 , etc.), including
present theoretical uncertainties on the relevant nonperturbative parameters
(such as
, etc.), including
present theoretical uncertainties on the relevant nonperturbative parameters
(such as 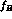 ), as well as the experimental statistical and systematical
uncertainties.
), as well as the experimental statistical and systematical
uncertainties.![]() Specifically, in the
histogram of Fig. 1, the solid line represents the predicted values of
Specifically, in the
histogram of Fig. 1, the solid line represents the predicted values of
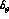 without any `cut' on the possible values of
without any `cut' on the possible values of 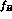 (see Ref. [1] for details), while the dashed one is obtained by
imposing such a `cut' (namely, by constraining
(see Ref. [1] for details), while the dashed one is obtained by
imposing such a `cut' (namely, by constraining 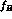 to the range of values
predicted by Lattice calculations). We recall that this `cut' would imply
to the range of values
predicted by Lattice calculations). We recall that this `cut' would imply
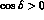 as the most likely possibility,
as the most likely possibility,  being
the CP violating CKM phase. As anticipated in Sec. 1, the predicted values of
being
the CP violating CKM phase. As anticipated in Sec. 1, the predicted values of
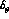 are of the order of some units per million. Fig. 2 is a
combined plot of
are of the order of some units per million. Fig. 2 is a
combined plot of 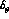 vs.
vs. 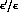 , the
solid and dashed lines representing the allowed contours with 5% and
68% probability, respectively, limiting to the case of the
, the
solid and dashed lines representing the allowed contours with 5% and
68% probability, respectively, limiting to the case of the 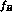 `cut' which
privileges
`cut' which
privileges 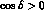 . One can remark from this figure that, for the
large values of
. One can remark from this figure that, for the
large values of 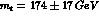 [15],
there is little correlation between the values of
[15],
there is little correlation between the values of 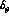 and
and
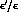 , whereas a rather strong correlation would have
occurred for small values of
, whereas a rather strong correlation would have
occurred for small values of 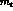 [6]. Also, Fig. 2 indicates that, while
[6]. Also, Fig. 2 indicates that, while 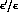 can vanish,
can vanish, 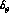 should be safely different from zero.
should be safely different from zero.
Finally, in Tab. 1 we summarize the numerical values for the various charge
asymmetries, as obtained from the procedure outlined above, in the case
 .
.
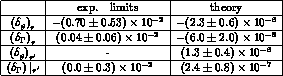
Table 1: Experimental values and theoretical predictions for the CP
violating asymmetries in  and
and  modes at lowest order in
modes at lowest order in
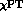 , including
, including 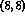 and
and 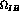 effects.
effects.
This table shows that the estimated CP violating asymmetries
are much larger for the
Dalitz plot slopes than for the total decay widths. Qualitatively, similar
results and orders of magnitudes for the asymmetry have been obtained in
[8], using the 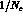 expansion at leading order.
expansion at leading order.
Eq. (7) is also useful for a simple discussion of possible higher
order 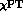 effects, which have been advocated in [16] as
the source of an enhancement of the asymmetry at the level of two orders of
magnitude. Indeed, higher order chiral corrections could be important,
because they can introduce further octet effective operators, to give
independent phases to the amplitudes of the two I=1 states. CP violating
interference of these two amplitudes would avoid the suppression factor
effects, which have been advocated in [16] as
the source of an enhancement of the asymmetry at the level of two orders of
magnitude. Indeed, higher order chiral corrections could be important,
because they can introduce further octet effective operators, to give
independent phases to the amplitudes of the two I=1 states. CP violating
interference of these two amplitudes would avoid the suppression factor
 in Eq. (8). Therefore, one could naively hope to gain an
enhancement factor
in Eq. (8). Therefore, one could naively hope to gain an
enhancement factor 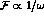 .
.
Actually, essentially following the discussion of Ref. [17], let us
reconsider Eq. (7) limiting ourselves to the first term only
(the second one may be neglected as it involves the 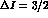 Hamiltonian in an essential way), and, after using Eq. (5),
rewrite it as
Hamiltonian in an essential way), and, after using Eq. (5),
rewrite it as
The first term in the square bracket is anyway suppressed by the combination of experimental amplitudes, which give
We can expand the second term, according to 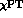 , into leading
, into leading
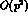 and next-to-leading
and next-to-leading 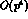 terms, as
terms, as
Therefore, to a good approximation, the relative size of the correction is
represented by the factor 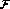 :
:
Coefficients are such that:
and therefore one derives:
More precisely, it can be seen that in the decomposition of the 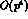
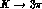 amplitudes into loop and counterterm contributions,
only the weak counterterms are relevant to (31). Indeed, in principle
loops can generate large
amplitudes into loop and counterterm contributions,
only the weak counterterms are relevant to (31). Indeed, in principle
loops can generate large 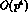 imaginary parts. However, these contributions
to the two
imaginary parts. However, these contributions
to the two 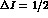 amplitudes must have the same weak phase (that of
the unique
amplitudes must have the same weak phase (that of
the unique 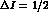
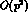 operator in (11)), and
therefore cannot build up a large CP violating interference
[6,17,18].
operator in (11)), and
therefore cannot build up a large CP violating interference
[6,17,18].
The rigorous inclusion of chiral loops and local counterterms for CP violating
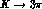 decays has not been accomplished yet, due to many unknown
constants. Nevertheless, chiral corrections are seen to be quite reasonable
for CP conserving amplitudes, introducing in that case effects of the order
of 40% or less (see [3]). Consequently, we can make the assumption
that the chiral expansion similarly works also for the CP violating
amplitudes (although not yet verified experimentally, this assumption seems
quite plausible). Thus, the order
decays has not been accomplished yet, due to many unknown
constants. Nevertheless, chiral corrections are seen to be quite reasonable
for CP conserving amplitudes, introducing in that case effects of the order
of 40% or less (see [3]). Consequently, we can make the assumption
that the chiral expansion similarly works also for the CP violating
amplitudes (although not yet verified experimentally, this assumption seems
quite plausible). Thus, the order 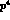 enhancement factor in (31)
should be expected to be of the order of
enhancement factor in (31)
should be expected to be of the order of 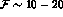 or so
(the upper figure corresponding to
the extreme case
or so
(the upper figure corresponding to
the extreme case 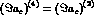 ),
which would enhance the predictions in Tab. 1 by an order of magnitude
at most. This is confirmed, e.g., by the findings of Ref. [19]
using the chiral
),
which would enhance the predictions in Tab. 1 by an order of magnitude
at most. This is confirmed, e.g., by the findings of Ref. [19]
using the chiral  -model, and of Ref. [8] in the framework of
the
-model, and of Ref. [8] in the framework of
the 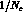 expansion.
expansion.