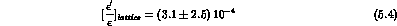Next: 6 Semileptonic amplitudes
Up: Chpter 1 Section 1
Previous: 4 decay amplitudesII
truecm
The parameter  is uniquely related to CP (and CPT) violation
in the transition amplitude, see Eq. (4.14). In the usual terminology,
is uniquely related to CP (and CPT) violation
in the transition amplitude, see Eq. (4.14). In the usual terminology,
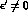 characterizes milli-weak theories,
i.e. theories in which the weak
interaction itself has a small but detectable CP violating component.
The mass mixing parameter,
characterizes milli-weak theories,
i.e. theories in which the weak
interaction itself has a small but detectable CP violating component.
The mass mixing parameter,  , arises as a 2
, arises as a 2 order weak
effect, in
which the CP-odd and CP-even parts combine to give the
order weak
effect, in
which the CP-odd and CP-even parts combine to give the 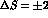 quantities M
quantities M and
and  .
.
Another, logically independent, possibility is that the observed
CP-violation is the 1 order manifestation of a new interaction with
order manifestation of a new interaction with
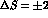 . In the mass matrix, the new interaction competes
with the 2
. In the mass matrix, the new interaction competes
with the 2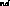 order weak contribution. Therefore, a very weak
interaction is required, of
strength
order weak contribution. Therefore, a very weak
interaction is required, of
strength 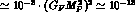 , to give rise
to the
observed CP violation. This is called the "superweak" theory [11], and
it has the obvious prediction that no CP-violation is visible in channels
available to 1
, to give rise
to the
observed CP violation. This is called the "superweak" theory [11], and
it has the obvious prediction that no CP-violation is visible in channels
available to 1 order weak transitions, i.e. it predicts
order weak transitions, i.e. it predicts
 .
.
Milliweak theories are in danger to contradict the very tight experimental
limits to the electric dipole of the neutron, a T- and P-violating,
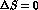 , effect. Unless a special cancellation occurs, we expect
any hadron to have an e.d.m. of the order of:
, effect. Unless a special cancellation occurs, we expect
any hadron to have an e.d.m. of the order of:
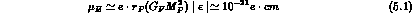
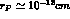 is the proton radius, which gives the general
dimension, the Fermi constant G
is the proton radius, which gives the general
dimension, the Fermi constant G is associated to P-violation while
is associated to P-violation while
 , in a milliweak theory, characterizes the generic strength of
T-violation. The present experimental upper bound to the neutron e.d.m.
is [12,13]:
, in a milliweak theory, characterizes the generic strength of
T-violation. The present experimental upper bound to the neutron e.d.m.
is [12,13]:
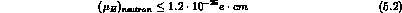
much too small to be compatible with (5.1), which therefore calls
for a very special cancellation.
The Standard, six flavour, Theory [14] is a milliweak theory in which
such a special cancellation does occur [15]. CP-violation
(rather, T-violation) arises because different components of the weak charged
current have non-vanishing relative phases. However, the one-loop correction to
the electromagnetic current of a given quark, e.g. the d-quark, is given by a
sum of terms in which each complex entry, corresponding to, say, 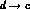 (V
(V ), is multiplied by the amplitude for the inverse process,
), is multiplied by the amplitude for the inverse process,
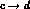 (V
(V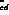 ). Thus, the correction is real and
the e.d.m vanishes to one loop, which brings the estimate (5.1) already down to
). Thus, the correction is real and
the e.d.m vanishes to one loop, which brings the estimate (5.1) already down to
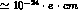 .
.
A further suppression is due to the fact that one can rotate away
the CP-violating phase when any two quark of the same charge are degenerate in
mass [15]. Thus, any CP-violating effect in the Standard theory must
involve light quark mass differences, which brings in powers of
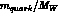 .
.
Finally, as shown in Ref. [16], the quark e.d.m. vanishes
also at two-loops, which brings in another factor of 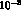 .
.
In conclusion, current estimates are that the e.d.m. of the neutron in the
Standard Theory is essentially unobservable [16]:
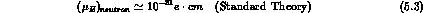
The above discussion underlines the importance of a positive measurement of
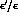 .
.
The first calculation of 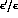 in the Standard Theory is
due to Gilman and Wise [17]. We summarize here the most recent
analyses[18,19]. The calculation of
in the Standard Theory is
due to Gilman and Wise [17]. We summarize here the most recent
analyses[18,19]. The calculation of
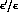 goes through several steps.
goes through several steps.
i) Determination of the effective weak, non-leptonic
Hamiltonian, 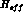 . The coefficients of the effective Hamiltonian
depend upon the chosen value of the subtraction point. Provided we choose
the subtraction point large enough, the result is dominated by
short-distance effects which, in QCD, are controlled by perturbation theory.
Different terms in
. The coefficients of the effective Hamiltonian
depend upon the chosen value of the subtraction point. Provided we choose
the subtraction point large enough, the result is dominated by
short-distance effects which, in QCD, are controlled by perturbation theory.
Different terms in 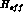 can be classified according to their
transformation properties under chiral SU(3)
can be classified according to their
transformation properties under chiral SU(3)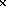 SU(3)[20].
The dominant term transforms as
SU(3)[20].
The dominant term transforms as 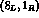 , corresponding to the familiar
octet-enhancement, while
, corresponding to the familiar
octet-enhancement, while 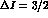 transitions are produced by a
transitions are produced by a
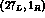 component. The
component. The 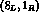 component has a complex coefficient
which arises, in the usual KM phase convention, because of t-quark exchange
in the so-called penguin diagrams. Electroweak penguin diagrams give rise
instead to
component has a complex coefficient
which arises, in the usual KM phase convention, because of t-quark exchange
in the so-called penguin diagrams. Electroweak penguin diagrams give rise
instead to 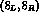 components, also with a complex coefficient.
components, also with a complex coefficient.
ii) The  term gives rise to a non-vanishing value
of
term gives rise to a non-vanishing value
of 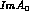 , thus giving a first contribution to Eq. (4.14).
Contributions to
, thus giving a first contribution to Eq. (4.14).
Contributions to 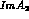 arise from two different sources.
The first is due to isospin breaking: the octet component contributes to
arise from two different sources.
The first is due to isospin breaking: the octet component contributes to
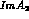 a term proportional
to the quark mass difference,
a term proportional
to the quark mass difference,  . Although this difference is small:
. Although this difference is small:
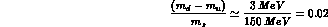
it is partly compensated by the fact that such a term appears in
Eq. (4.14) divided by 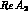 and is therefore enhanced by a
factor of
and is therefore enhanced by a
factor of 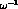 with respect to the previous one, see Eq. (4.5). A
second contribution to
with respect to the previous one, see Eq. (4.5). A
second contribution to 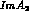 arises from the
arises from the
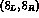 component. The small Wilson coefficient with which it appears in
component. The small Wilson coefficient with which it appears in
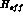 is partly compensated by
the factor
is partly compensated by
the factor 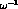 and also by the fact that chiral symmetry does not
require the matrix element of the
and also by the fact that chiral symmetry does not
require the matrix element of the 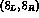 to vanish for vanishing external
momenta, as is the case for both the
to vanish for vanishing external
momenta, as is the case for both the 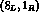 and
and 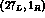 . The raising
with the t-quark mass of the Wilson coefficient of the
. The raising
with the t-quark mass of the Wilson coefficient of the 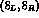 term is
responsible for the decrease of
term is
responsible for the decrease of 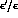 .
.
iii) Matrix elements of the effective Hamiltonian are
parametrized in terms of the so-called B-factors, scale factors which measure
the deviation of the true matrix element from the one computed in the vacuum
insertion approximation. At present, systematic calculations of the B-factors
have been carried on with lattice QCD, QCD sum rules and the
expansion in the inverse of the number of colours, 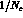 .
.
Predictions of 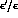 vs. the top-quark mass are
discussed later in this
report [3]. For illustration, we show in Fig. 1 the theoretical
prediction, for B-factors computed in lattice QCD.
vs. the top-quark mass are
discussed later in this
report [3]. For illustration, we show in Fig. 1 the theoretical
prediction, for B-factors computed in lattice QCD.
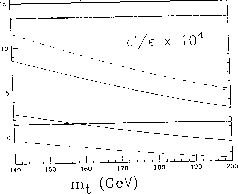
Figure 1: 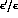 as function of
as function of 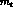 , obtained by
applying the
, obtained by
applying the 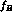 -cut [3]. The zones delimited by
the solid and dashed curves represent the allowed regions containing
respectively 68% and 95% of the generated events. The region between the
two double lines is the experimental result coming from E731, see text.
-cut [3]. The zones delimited by
the solid and dashed curves represent the allowed regions containing
respectively 68% and 95% of the generated events. The region between the
two double lines is the experimental result coming from E731, see text.
The value of 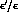 is generally predicted in the 10
is generally predicted in the 10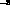 range. A very small value results for
range. A very small value results for 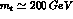 , due to
the electroweak penguin effects. The top-quark mass recently discovered by
CDF [21] is:
, due to
the electroweak penguin effects. The top-quark mass recently discovered by
CDF [21] is:

For this value, the best prediction of lattice QCD calculation is
[3]:
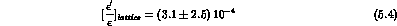



Next: 6 Semileptonic amplitudes
Up: Chpter 1 Section 1
Previous: 4 decay amplitudesII
Carlos E.Piedrafita
 is uniquely related to CP (and CPT) violation
in the transition amplitude, see Eq. (4.14). In the usual terminology,
is uniquely related to CP (and CPT) violation
in the transition amplitude, see Eq. (4.14). In the usual terminology,
 characterizes milli-weak theories,
i.e. theories in which the weak
interaction itself has a small but detectable CP violating component.
The mass mixing parameter,
characterizes milli-weak theories,
i.e. theories in which the weak
interaction itself has a small but detectable CP violating component.
The mass mixing parameter,  , arises as a 2
, arises as a 2 order weak
effect, in
which the CP-odd and CP-even parts combine to give the
order weak
effect, in
which the CP-odd and CP-even parts combine to give the  quantities M
quantities M and
and  .
.
 order manifestation of a new interaction with
order manifestation of a new interaction with
 . In the mass matrix, the new interaction competes
with the 2
. In the mass matrix, the new interaction competes
with the 2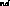 order weak contribution. Therefore, a very weak
interaction is required, of
strength
order weak contribution. Therefore, a very weak
interaction is required, of
strength 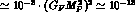 , to give rise
to the
observed CP violation. This is called the "superweak" theory [
, to give rise
to the
observed CP violation. This is called the "superweak" theory [ order weak transitions, i.e. it predicts
order weak transitions, i.e. it predicts
 .
.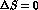 , effect. Unless a special cancellation occurs, we expect
any hadron to have an e.d.m. of the order of:
, effect. Unless a special cancellation occurs, we expect
any hadron to have an e.d.m. of the order of:
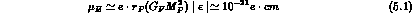
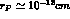 is the proton radius, which gives the general
dimension, the Fermi constant G
is the proton radius, which gives the general
dimension, the Fermi constant G is associated to P-violation while
is associated to P-violation while
 , in a milliweak theory, characterizes the generic strength of
T-violation. The present experimental upper bound to the neutron e.d.m.
is [
, in a milliweak theory, characterizes the generic strength of
T-violation. The present experimental upper bound to the neutron e.d.m.
is [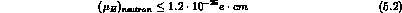
 (V
(V ), is multiplied by the amplitude for the inverse process,
), is multiplied by the amplitude for the inverse process,
 (V
(V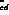 ). Thus, the correction is real and
the e.d.m vanishes to one loop, which brings the estimate (5.1) already down to
). Thus, the correction is real and
the e.d.m vanishes to one loop, which brings the estimate (5.1) already down to
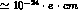 .
.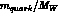 .
.
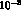 .
.
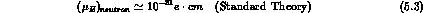
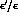 .
.
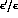 in the Standard Theory is
due to Gilman and Wise [
in the Standard Theory is
due to Gilman and Wise [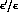 goes through several steps.
goes through several steps.
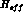 . The coefficients of the effective Hamiltonian
depend upon the chosen value of the subtraction point. Provided we choose
the subtraction point large enough, the result is dominated by
short-distance effects which, in QCD, are controlled by perturbation theory.
Different terms in
. The coefficients of the effective Hamiltonian
depend upon the chosen value of the subtraction point. Provided we choose
the subtraction point large enough, the result is dominated by
short-distance effects which, in QCD, are controlled by perturbation theory.
Different terms in 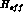 can be classified according to their
transformation properties under chiral SU(3)
can be classified according to their
transformation properties under chiral SU(3) SU(3)[
SU(3)[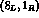 , corresponding to the familiar
octet-enhancement, while
, corresponding to the familiar
octet-enhancement, while 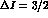 transitions are produced by a
transitions are produced by a
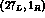 component. The
component. The 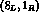 component has a complex coefficient
which arises, in the usual KM phase convention, because of t-quark exchange
in the so-called penguin diagrams. Electroweak penguin diagrams give rise
instead to
component has a complex coefficient
which arises, in the usual KM phase convention, because of t-quark exchange
in the so-called penguin diagrams. Electroweak penguin diagrams give rise
instead to 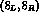 components, also with a complex coefficient.
components, also with a complex coefficient.
 term gives rise to a non-vanishing value
of
term gives rise to a non-vanishing value
of 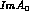 , thus giving a first contribution to Eq. (4.14).
Contributions to
, thus giving a first contribution to Eq. (4.14).
Contributions to 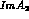 arise from two different sources.
The first is due to isospin breaking: the octet component contributes to
arise from two different sources.
The first is due to isospin breaking: the octet component contributes to
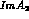 a term proportional
to the quark mass difference,
a term proportional
to the quark mass difference,  . Although this difference is small:
. Although this difference is small:
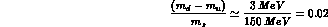
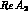 and is therefore enhanced by a
factor of
and is therefore enhanced by a
factor of 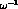 with respect to the previous one, see Eq. (4.5). A
second contribution to
with respect to the previous one, see Eq. (4.5). A
second contribution to 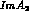 arises from the
arises from the
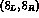 component. The small Wilson coefficient with which it appears in
component. The small Wilson coefficient with which it appears in
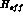 is partly compensated by
the factor
is partly compensated by
the factor 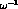 and also by the fact that chiral symmetry does not
require the matrix element of the
and also by the fact that chiral symmetry does not
require the matrix element of the 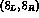 to vanish for vanishing external
momenta, as is the case for both the
to vanish for vanishing external
momenta, as is the case for both the 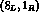 and
and 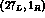 . The raising
with the t-quark mass of the Wilson coefficient of the
. The raising
with the t-quark mass of the Wilson coefficient of the 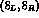 term is
responsible for the decrease of
term is
responsible for the decrease of 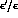 .
.
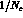 .
.
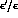 vs. the top-quark mass are
discussed later in this
report [
vs. the top-quark mass are
discussed later in this
report [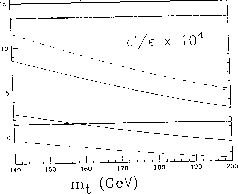
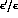 as function of
as function of 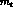 , obtained by
applying the
, obtained by
applying the 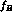 -cut [
-cut [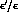 is generally predicted in the 10
is generally predicted in the 10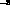 range. A very small value results for
range. A very small value results for 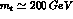 , due to
the electroweak penguin effects. The top-quark mass recently discovered by
CDF [
, due to
the electroweak penguin effects. The top-quark mass recently discovered by
CDF [