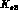 decays of
decays of 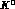 and
and 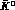 . On general grounds,
there are 4 independent matrix elements, related to the (complex) form factors
of the transitions:
truecm
. On general grounds,
there are 4 independent matrix elements, related to the (complex) form factors
of the transitions:
truecm
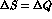 :
:
truecm
We focus on 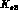 decays of
decays of 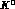 and
and 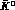 . On general grounds,
there are 4 independent matrix elements, related to the (complex) form factors
of the transitions:
truecm
. On general grounds,
there are 4 independent matrix elements, related to the (complex) form factors
of the transitions:
truecm
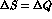 :
:
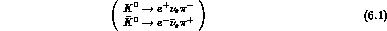
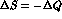 :
:
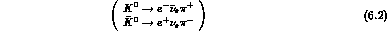
Time-reversal relates each form factor to its complex conjugate, CP relates
K to
to 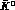 form factors. This suggests to parametrize the amplitudes
according to:
form factors. This suggests to parametrize the amplitudes
according to:
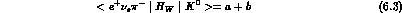
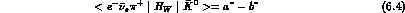
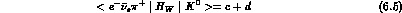
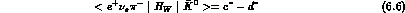
a and b (c and d) obey the same symmetry properties as the
non-leptonic amplitudes 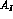 and
and 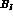 (see Tab. 2), i.e.: b and d are CPT
violating, imaginary parts are all T-violating; c and d describe possible
violations of the
(see Tab. 2), i.e.: b and d are CPT
violating, imaginary parts are all T-violating; c and d describe possible
violations of the 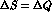 rule. We consider
rule. We consider
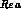 of order unity, and keep first order terms in all the
other quantities.
of order unity, and keep first order terms in all the
other quantities.
Of course, one should introduce analogous amplitudes for muonic decays, but we will leave this understood, in the following, to avoid a too heavy notation.
The following notations are also used [2]:

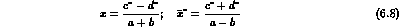
with:
truecm
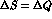 exact:
exact:

CPT exact:
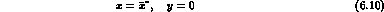
T exact:
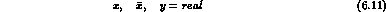
CP exact:
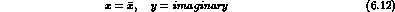
For convenience, we shall also define:
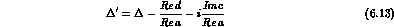
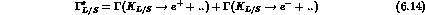
with  defined in Eqs. (1.19) and (1.20) and:
defined in Eqs. (1.19) and (1.20) and:

The following relations are immediate:
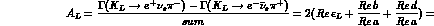
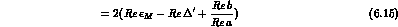
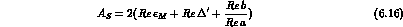
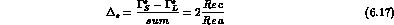
There are in all four semileptonic rates, which can be expressed in terms
of the three combinations given above plus the average rate, which determines
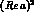 . In addition, to study the correlated decays of
the
. In addition, to study the correlated decays of
the 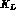 -
-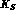 pair produced at a
pair produced at a 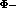 factory, it is convenient to
introduce the complex quantities:
factory, it is convenient to
introduce the complex quantities:
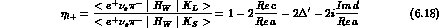
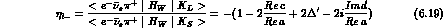
In the Standard Theory, CPT and CP are conserved in semileptonic processes
and the 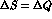 rule is obeyed to a very good precision [22],
with (
rule is obeyed to a very good precision [22],
with ( is the relative strength of the octet non-leptonic
amplitude):
is the relative strength of the octet non-leptonic
amplitude):
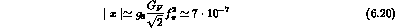
In the current x current picture there is, in fact, little space for the violation of these symmetries, given our very good knowledge of the currents themselves.
Violation of CP or of the 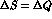 rule could arise from
contact interactions of quark and leptons (e.g. in composite models) and one
should keep an open mind on the possible presence of anomalies in the
semileptonic amplitudes. However,
rule could arise from
contact interactions of quark and leptons (e.g. in composite models) and one
should keep an open mind on the possible presence of anomalies in the
semileptonic amplitudes. However, 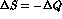 transitions require
hadronic operators transforming as 10 + 27 of flavour SU(3), see e.g. the
second paper of Ref. [22], that can be induced only by effective quark
and lepton operators of dimension higher than four. A typical example is:
transitions require
hadronic operators transforming as 10 + 27 of flavour SU(3), see e.g. the
second paper of Ref. [22], that can be induced only by effective quark
and lepton operators of dimension higher than four. A typical example is:
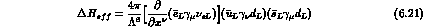
with  the compositeness scale, which leads to the (rather
generous) estimate:
the compositeness scale, which leads to the (rather
generous) estimate:
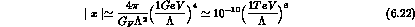
The result (6.22) justifies the neglect of 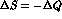 amplitudes,
still keeping open the possibility of CPT violation.
amplitudes,
still keeping open the possibility of CPT violation.
For the sake of brevity, the case in which semileptonic amplitudes are assumed
to conserve both CPT and the 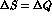 rule will be called
Scheme I, in the following. Scheme II will be the case in which CPT
is relaxed, still keeping exact the
rule will be called
Scheme I, in the following. Scheme II will be the case in which CPT
is relaxed, still keeping exact the 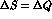 rule. We shall also
comment on Scheme III, where Eqs. (6.3) to (6.6) are considered in full
generality.
rule. We shall also
comment on Scheme III, where Eqs. (6.3) to (6.6) are considered in full
generality.