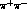 and
and
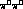 channels:
channels:
truecm
From Eqs. (2.3) and (2.4) and the isospin Clebsch-Gordan
coefficients, one finds the decay amplitudes in the 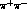 and
and
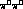 channels:
channels:![]()
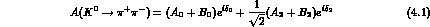
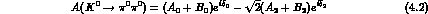
For 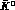 amplitudes,
amplitudes, 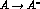 ,
, 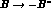 . Also:
. Also:
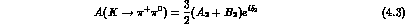
From these formulae and from the experimental 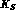 and
and 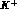 decay rates
we can derive the values of the CP and CPT-conserving amplitudes:
decay rates
we can derive the values of the CP and CPT-conserving amplitudes:
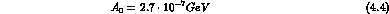
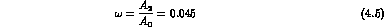
as well as:
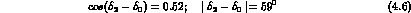
The value of the phase is in reasonable agreement with the one found
from pion production in  -Nucleon scattering and in
-Nucleon scattering and in 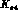 decay:
decay:
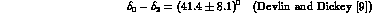
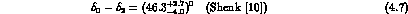
After these preliminaries, we proceed to derive the formulae for the
2 decays of K
decays of K . One defines:
. One defines:
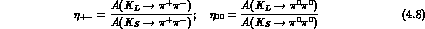
and finds, from Eqs. (1.13) and (4.1-2) (Wu-Yang convention is used
throughout, terms of second order in CP/CPT violation and first order
multiplied by 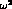 are neglected):
are neglected):

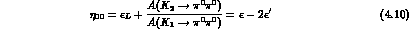
with:
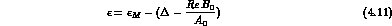
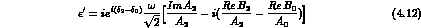
Eqs. (4.9) and (4.10) are formally identical to those of the exact CPT
limit, but with a different relation between  and the mass mixing
parameters, and with an additional contribution of the B's to
and the mass mixing
parameters, and with an additional contribution of the B's to  .
.
In the limit of vanishing  and B, one obtains in (4.12) the usual
expression for
and B, one obtains in (4.12) the usual
expression for  , in the notation appropriate to the Wu-Yang
convention. As noted before, given the amplitudes computed with a different
phase convention, e.g. with the usual KM phases, we obtain the amplitudes in the
Wu-Yang frame by making, for any
, in the notation appropriate to the Wu-Yang
convention. As noted before, given the amplitudes computed with a different
phase convention, e.g. with the usual KM phases, we obtain the amplitudes in the
Wu-Yang frame by making, for any 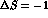 amplitude X, the
replacement:
amplitude X, the
replacement:

In this way, we obtain from Eq. (4.12) the phase-convention independent expression:
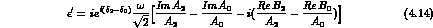
The structure of Eq. (4.14) can be read very simply, with reference to
the definition of  given in Eq. (4.9). The factor
given in Eq. (4.9). The factor
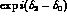 arises from the final state interaction, the
dominant final states being I=2 and I=0 for the numerator and denominator
of the ratio in Eq. (4.9), respectively. The further factor of i arises
because
arises from the final state interaction, the
dominant final states being I=2 and I=0 for the numerator and denominator
of the ratio in Eq. (4.9), respectively. The further factor of i arises
because  , being CP violating, must violate time-reversal
in a CPT conserving theory (i.e. be imaginary, apart from the final state
interaction phases). CPT violation, indeed, appears as a further,
T-conserving, imaginary contribution to the square bracket in Eq. (4.14).
, being CP violating, must violate time-reversal
in a CPT conserving theory (i.e. be imaginary, apart from the final state
interaction phases). CPT violation, indeed, appears as a further,
T-conserving, imaginary contribution to the square bracket in Eq. (4.14).