


Next: 2.3 Transition F.F. for
Up: 2 How many independent
Previous: 2.1 Elastic F.F. for
In addition to the two independent four-momenta p and 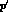 ,
in this case the four
,
in this case the four 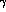 -matrices,
-matrices, 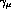 , can be used
to construct a third type of vectorial structure, as required by
Lorentz invariance.
Other combinations of
, can be used
to construct a third type of vectorial structure, as required by
Lorentz invariance.
Other combinations of 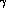 -matrices
with four-momenta can be easily seen to reduce to the previous three
forms using
the Dirac equation for the external, on-shell spin 1/2 baryons. On the
other hand, as before, current conservation requires the vanishing of a
term proportional to
-matrices
with four-momenta can be easily seen to reduce to the previous three
forms using
the Dirac equation for the external, on-shell spin 1/2 baryons. On the
other hand, as before, current conservation requires the vanishing of a
term proportional to 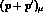 , thus implying that only two
independent form factors are allowed, i.e.,
, thus implying that only two
independent form factors are allowed, i.e.,
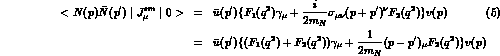
The first line in the previous eq. contains the so-called Dirac and
Pauli form factors 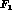 and
and 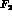 . At
. At 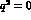 , they are respectively
normalized to the electric charge of the baryon N (in units of the
proton charge e) and to its anomalous magnetic moment (in units of
, they are respectively
normalized to the electric charge of the baryon N (in units of the
proton charge e) and to its anomalous magnetic moment (in units of
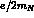 ). Their combinations
). Their combinations
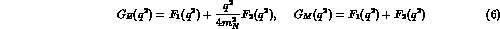
(the latter appearing
in the second of eqs.(5) and illustrating the above mentioned
reduction procedure via Gordon decomposition of Dirac currents),
are the Sachs form factors and verify the
interesting property of being equal at the production threshold,
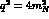 .
.
Carlos E.Piedrafita
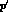 ,
in this case the four
,
in this case the four 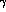 -matrices,
-matrices, 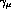 , can be used
to construct a third type of vectorial structure, as required by
Lorentz invariance.
Other combinations of
, can be used
to construct a third type of vectorial structure, as required by
Lorentz invariance.
Other combinations of 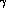 -matrices
with four-momenta can be easily seen to reduce to the previous three
forms using
the Dirac equation for the external, on-shell spin 1/2 baryons. On the
other hand, as before, current conservation requires the vanishing of a
term proportional to
-matrices
with four-momenta can be easily seen to reduce to the previous three
forms using
the Dirac equation for the external, on-shell spin 1/2 baryons. On the
other hand, as before, current conservation requires the vanishing of a
term proportional to 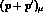 , thus implying that only two
independent form factors are allowed, i.e.,
, thus implying that only two
independent form factors are allowed, i.e.,
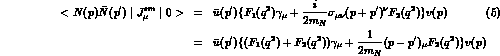
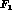 and
and 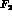 . At
. At 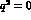 , they are respectively
normalized to the electric charge of the baryon N (in units of the
proton charge e) and to its anomalous magnetic moment (in units of
, they are respectively
normalized to the electric charge of the baryon N (in units of the
proton charge e) and to its anomalous magnetic moment (in units of
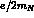 ). Their combinations
). Their combinations
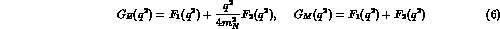
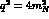 .
.