 is
most conveniently expressed in terms of the Sachs form
factors as
is
most conveniently expressed in terms of the Sachs form
factors as
The CM differential cross-section for  is
most conveniently expressed in terms of the Sachs form
factors as
is
most conveniently expressed in terms of the Sachs form
factors as

From this eq. and working above threshold, proton, neutron
and other baryon form factors can, in principle, be extracted in an
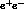 -machine. However, being far from the narrow resonance region,
the cross-section is rather low and statitistics is hard to collect.
Assuming the above mentioned equality of magnetic and electric
Sachs form factors at threshold, early measurements have given information
with large errors. Recently, more precise data have been produced and
also the neutron form factor has been measured for the first time.
These results are shown in Fig.(7)
-machine. However, being far from the narrow resonance region,
the cross-section is rather low and statitistics is hard to collect.
Assuming the above mentioned equality of magnetic and electric
Sachs form factors at threshold, early measurements have given information
with large errors. Recently, more precise data have been produced and
also the neutron form factor has been measured for the first time.
These results are shown in Fig.(7)
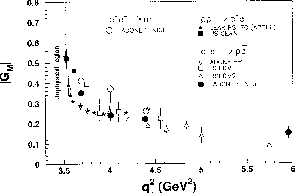
Figure 7: The proton and neutron e.m. form factors as a function of  .
.
On the other hand, one has excellent data from elastic e N-scattering
for 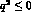 . Here, both the
. Here, both the 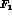 and
and 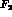 (or
(or 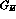 and
and 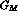 )
form factors can be separately measured for both protons and neutrons,
as well as for their isoscalar or isovector combinations. We don't discuss
these results explicitly, being only of secondary interest for Daphne, but
simply recall that a reasonable description of these data can be
achieved by a ``universal" dipole fit
)
form factors can be separately measured for both protons and neutrons,
as well as for their isoscalar or isovector combinations. We don't discuss
these results explicitly, being only of secondary interest for Daphne, but
simply recall that a reasonable description of these data can be
achieved by a ``universal" dipole fit
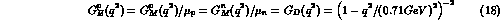
for 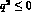 .
.
The corresponding electric and magnetic charge radii are found to be in
the range of 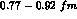 , i.e., only moderately above the charge
radii for charged pseudoscalars. Further details and references for
nucleon form factors can be found in refs. [3] and [12].
Concerning the asymptotic behaviour expected from the quark
counting rules [5], it coincides with the dipole formula
, i.e., only moderately above the charge
radii for charged pseudoscalars. Further details and references for
nucleon form factors can be found in refs. [3] and [12].
Concerning the asymptotic behaviour expected from the quark
counting rules [5], it coincides with the dipole formula
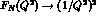 .
.